MPRT - Modified planetary robotics transmission

I both under-extruded and set values which were too large for backlash/clearance on my proof of concept.

The under-extrusion was mostly on purpose.  I didn't need this to handle any kind of load, and under-extrusion of gears produces perfect profiles with far less thought.

However... the backlash/clearance values I used were from another project where I had also planned to intentionally over-extrude everything to ensure I had completely solid gears for my high-load application.

So the result is my gears don't mesh well and have massive clearance/backlash.

It does work though, but I won't do a video of it looking like this.

It probably didn't help that I also intentionally doubled the backlash value for the output gear to ensure it wouldn't bind as it will be running a less than perfect involute gear profile.  I also increased the tooth pitch (which means smaller teeth) so I'm in uncharted territory for printing these.  These teeth are smaller than I have ever printed at 0.4mm nozzle size.

So... 'doing the needful' as my co-workers of Indian descent like to say.  :)

I'm beginning to deduce some of the magic required here to make the gears mesh.

I stumbled upon a compatible gear set by accident originally, but now I think I understand what is actually going on.

The rules:

• The sun gear tooth count must be divisible by both 2 and <num planets>.
• The ring gear tooth count must be divisible by both 2 and <num planets>.
• Stationary ring gear tooth count - sun tooth count must be an even number.
• Output ring gear tooth count = Ring tooth count +- <num planets>, with adjusted gear pitch to equal the stationary ring gear diameter.  The adjustment to diametrical pitch = <ring_tooth_pitch>*(ring_tooth_count> +-<num planets> )/<ring_tooth_count>

So basically... for 3 planets I will need multiples of 6 for both the sun and ring gear tooth count.

For the test I've settled on 18 sun teeth, 60 ring teeth, and 57 output teeth.  

Planet tooth count is a always a function of the sun/ring tooth count and ends up being = (<ring_tooth_count> - <sun_tooth_count>)/2.  So for this test, they will have 21 teeth.

I increased my pitch a little so it still fits on a Nema 23, from 0.965 to 1.05 and I'm using a pressure angle of 24.

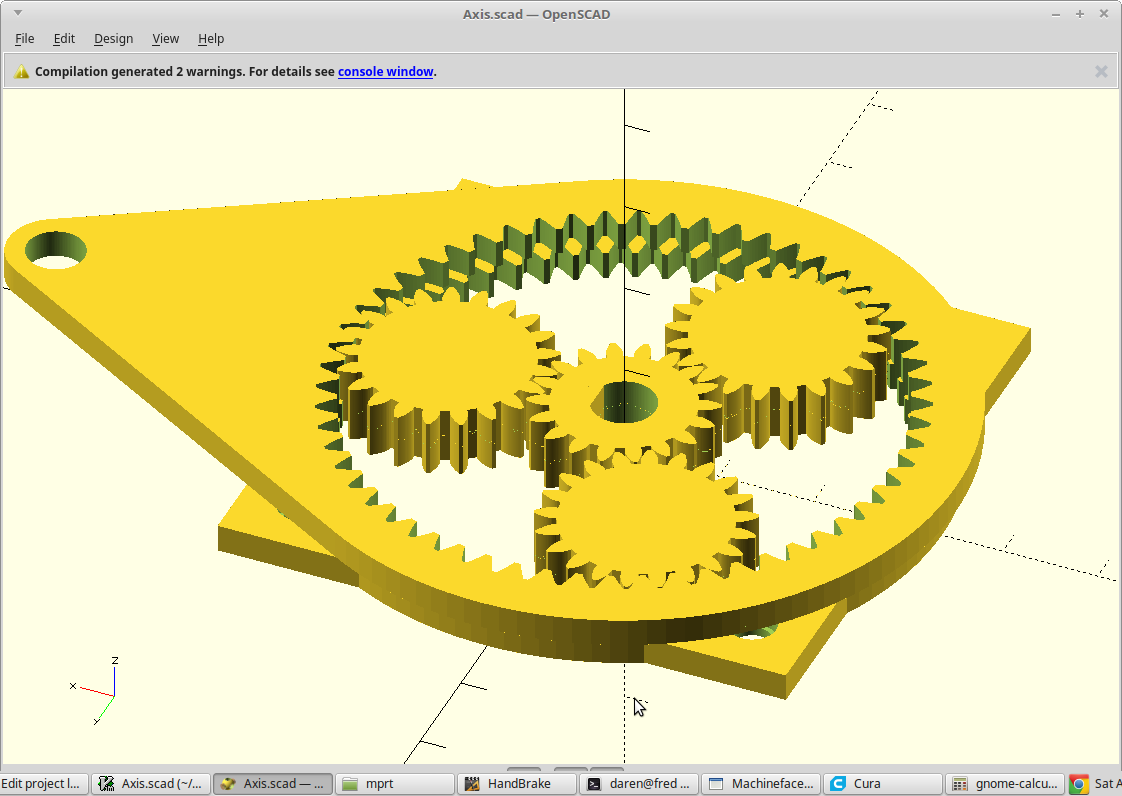
This is what that looks like.

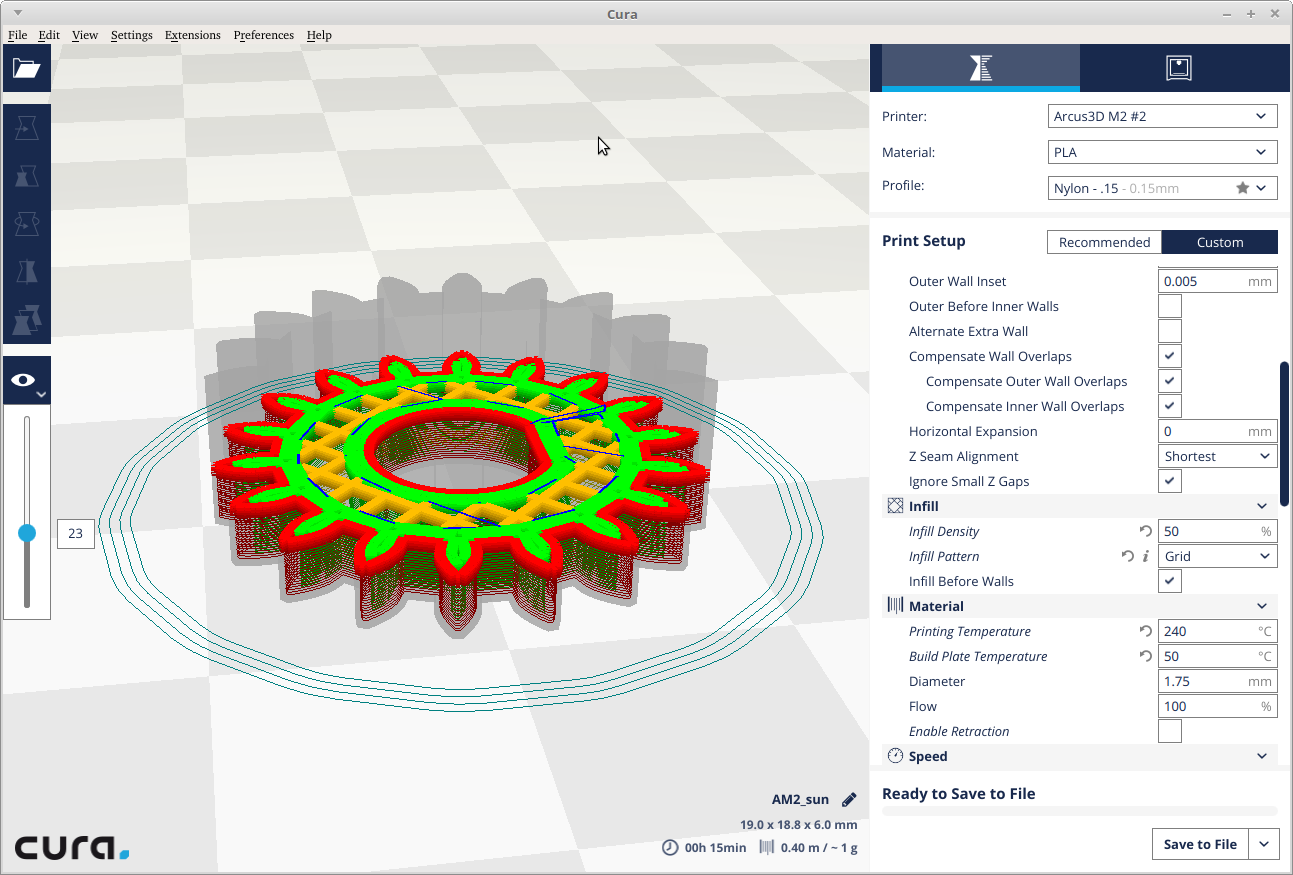
Sliced.

Printing.

I re-used a previous source to build this one, so it is a complete mess with most of it commented out.

However, I'm putting it up for the benefit of those who want to see it.  Don't judge me.  :)

Also, if you want to be a part of working this out, ask.