Now that the controller chip has been chosen, there are a lot parts to pick based on datasheet requirements. Most of these choices are straightforward, but some, such as the choice of switching frequency, need some consideration of the limits of other parts choices, and the compensation components, which will require extensive theoretical development or some intuition coupled with experimental evaluation.

Converter design parameters

• Input voltage: 5 to 12 V
• Output voltage: 170 V
• Maximum output current: 30 mA

Switching frequency

The way I picked the switching frequency was to work backwards from the maximum inductor current ripple limit. The results in the details section rely on the idea that the average inductor current can be substituted for the time-varying result. If this assumption, called the small-ripple approximation, is no longer true, than more complicated mathematics must be applied, as is the case when the inductor current goes to zero during the switching cycle, and the converter is said to be operating in discontinuous conduction mode (DCM).

During the on-state of the switching cycle, the voltage applied from the input source ramps the current in the inductor. For an inductor, v = L (di/dt), so the slope of this ramp is v/L. The peak-to-peak ripple is this slope times the amount of time the switch is on and this voltage is applied:

Solving for the switching frequency (reciprocal of the period T):

The maximum duty cycle and current occur at the lowest input voltage (5 V). The computed duty cycle and inductor current are D=.773 and IL = 1.4 A. I'd like to keep the ripple to less than 40% of the average current, so plugging values in, the resulting switching frequency is 366 kHz. I rounded this to 350 kHz and used the timing resistor formula in the LM5155 datasheet to obtain a timing resistance of 62 kΩ.

Feedback resistors

The voltage reference on the LM5155 is an even 1 V, so I need to reduce the output voltage of 170 V to 1 V, preferably without burning much current since this converter is designed to supply 30 mA. As luck would have it, there is an E96 value combo that gives us an exact 1/170 resistor divider and draws less than 1 mA at 170 V: use a 1.69 MΩ & 10 kΩ divider.

Undervoltage lockout (UVLO)

The LM5155 has a feature to adjust the UVLO levels that shutdown the converter, with  configurable hysteresis. This isn't important for an evaluation board that will checked out on the bench, but I decided to set an on value of 4.75 V and off value of 4.6 V. The datasheet has a formula to set the resistor divider on the UVLO pin, which yields R1 (top) = 18.7 kΩ and R2 (bottom) = 8.66 kΩ - these are rounded to the closest E96 values.

Soft start

The soft start circuit in the LM5155 charges the voltage reference using a 10 µA current source into the attached external capacitor. Once the voltage on the SS pin hits 1 V, the internal voltage reference takes over, so the soft start time is determined by the time it takes to charge the capacitor to 1 V, so 10 nF gives a startup ramp time of 1 ms. I don't consider this critical for a evaluation board powered by a bench power supply, and some datasheet examples used 22 nF, so I picked this as a starting point.

Current sense network

This section relies on results from the theory of current programmed control that are not immediately obvious. An excellent reference on current programmed mode is chapter 12 of Fundamentals of Power Electronics by Erickson and Maksimović.

The LM5155 uses peak current control (also called current programmed mode) to set the duty cycle. This offers overcurrent protection and also improves the stability of the feedback loop. The inductor current is sensed by observing the voltage at a low-side shunt resistor. When the voltage level at the CS pin hits the controller's threshold, the MOSFET turns off for the rest of the switching cycle.

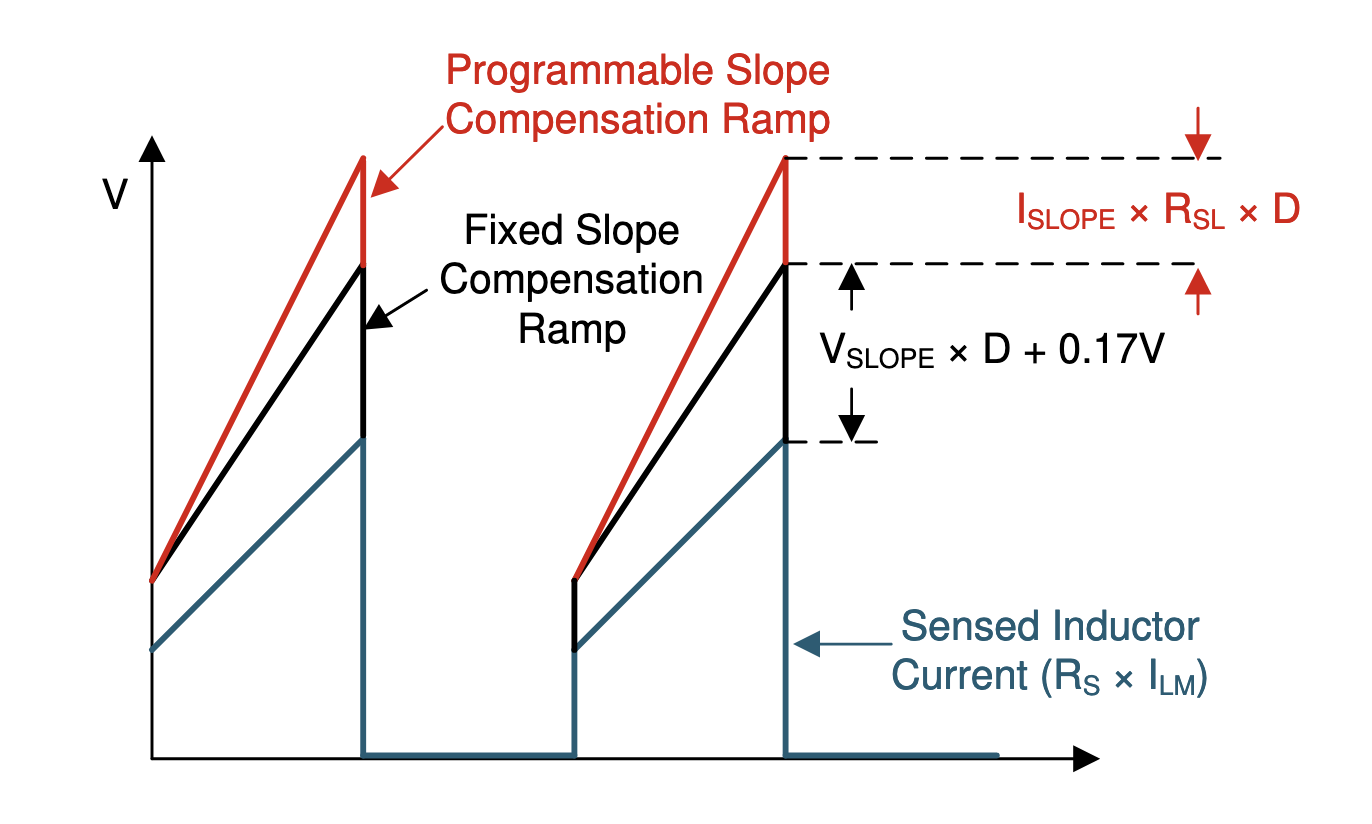
According to the control theory of the current programmed mode, there is an inherent instability when the resulting duty cycle > 1/2. To fix this problem, an artificial ramp is added to the sensed current (or equivalently, the ramp is subtracted from the threshold limit). The same result requires the slope of artificial ramp to be at least half the slope of the inductor current in the off-state. From the off-state diagram in the details section, the off-state voltage across the magnetizing inductance is -V/n, so the magnitude of the off-state current slope is V/(n*L). The requirement for the artificial ramp can be expressed like this:

Here Rs (the sensor resistor) is included since all currents are observed relative to the sense resistor. The LM5155 datasheet doesn't state the artificial ramp slope, but it gives the amplitude of the voltage ramp, which is 40 mV. As slope = rise / run, the right hand side can be replaced with the magnitude of the ramp divided by the period of a switching cycle (or multiplied by the switching frequency):

This places a limit on the sense resistor to achieve stability. Plugging in the values from the datasheet and the design so far, Rs must be less than 16 mΩ. Derating this value by 20% as recommended in the datasheet yields Rs < 14 mΩ. On the other hand, when the peak inductor current hits the threshold,

The DA2032 transformer's saturation current is 3 A, so the required sense resistor is 33 mΩ.

Is all hope lost? No! By adding a series resistor to the CS pin, additional artificial ramp can be added. An internal 30 µA current source drives a voltage ramp across this series resistance. To find the right values for the sense resistor and slope resistor, two equations must be solved simultaneously for Rs and RSL:

In the above, beta is the slope factor, which the datasheet recommends using 0.82 (recall 0.5 is the minimum for stability). Solving for the same maximum current condition yields Rs = 18 mΩ and RSL = 1 kΩ.

Additionally, the LM5155 datasheet recommends a low-pass filter on the CS pin. They state this design recommendation for the RC filter:

All this means is that when the sensed current drops to zero in the off-state, the filter should get at least 3 x the filter time constant to discharge the capacitor. Additionally, it makes sense to have R be small compared to RSL since it appears in series with it. I picked R = 20 Ω, which requires C < 11 nF at the maximum duty cycle of .773. I chose C = 4.7 nF for an extra margin.