In the last log I showed a few computational issues:

• The motion primitives calculations are too slow (around 1ms after some initial optimization)
• The control function is too slow (around 250us)
• The control function is not called at a consistent rate (uses a software timer)

This log explains some updates I did to make things faster and more consistent. Some are still works in progress, but it is looking promising.

---

Pre-calculations

All of the motion primitives are set up as cyclical motions defined in Cartesian space. Both linear and quadratic Bezier curves are supported. I realized with typical control periods, and primitive calculation rates it would not be difficult to pre-calculate the positions, and then simply use a lookup-table when it is running to get the position. I implemented this right away. In addition, for simple position control through these profiles, inverse kinematics is required to calculate the motor positions. I also added a layer to pre-calculate the motor positions (in ticks, as integers). Now that everything was set up as simple integer lookup tables, motion primitives with position control are very fast. My timing showed that this calculation required only about 34us, around 30X faster than the original Bezier VMC setup.

---

Integer PID Controller

To make this control method even faster, I also had to set up the PID controller as integer only. Care must be taken when doing this, as it is easy to get odd rounding, overflow, and underflow issues with integer math. Thankfully, for position control my inputs and outputs were already scaled to be in the thousands typically, and the controller gains were reasonably high. Furthermore, the inputs were actually integers cast to floats, and the output was a float cast back to an integer. I therefore thought that I should be able to achieve decent control with a simple implementation. The code below shows the implementation. There are only two parts that are non-standard. First, the speed is filtered according to this great Hackaday project. In addition, my typical Ki for position control was 0.004. Therefore, I added an integral shift option so that effectively small Ki values are possible.

 int32_t calculate_integer_pid(pid_integer_control_t * pid, int32_t setpoint, int32_t current_position)
 {
	static int32_t speed_old_z = 0;

	int32_t error = setpoint - current_position;

	int32_t speed_z = speed_old_z - speed_old_z >> pid->filter_shift + (current_position - pid->last_position);
	pid->speed = speed_z >> pid->filter_shift;

	speed_old_z = speed_z;

	pid->integral += error;

	if(pid->integral > pid->integral_max)
	{
		pid->integral = pid->integral_max;
	}
	else if(pid->integral < pid->integral_min)
	{
		pid->integral = pid->integral_min;
	}

	int32_t cmd = pid->kp * error + pid->kd * pid->speed + (pid->ki * pid->integral >> pid->integral_shift);

	if(cmd > pid->cmd_max)
	{
		cmd	= pid->cmd_max;
	}
	else if(cmd < pid->cmd_min)
	{
		cmd = pid->cmd_min;
	}

	pid->last_error = error;
	pid->last_position = current_position;
	return cmd;
 }

 With this implementation used for position control, the position control loop is now about 79us, about 3X faster than before. More importantly, it seems to work just as well.

---

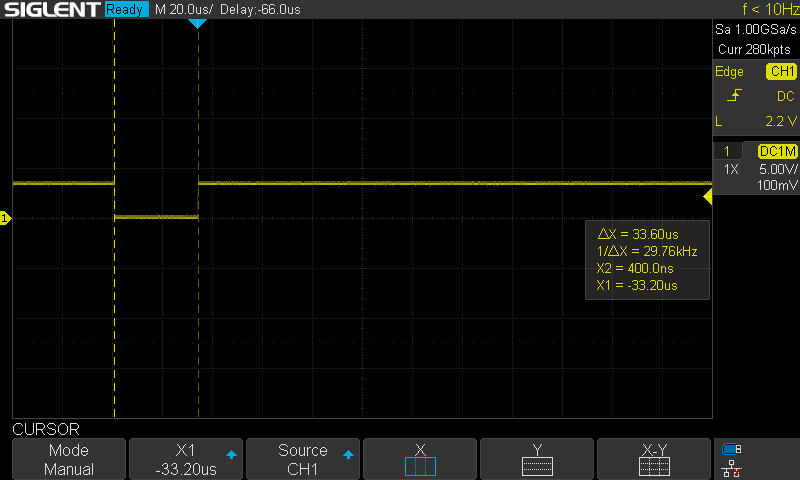
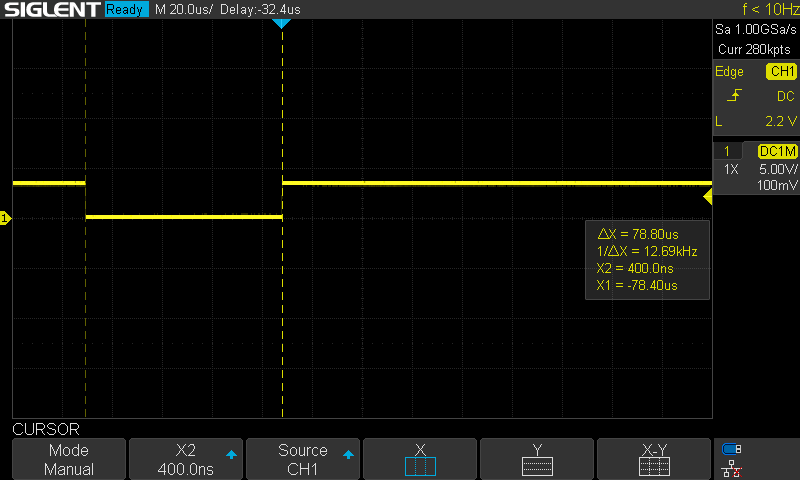
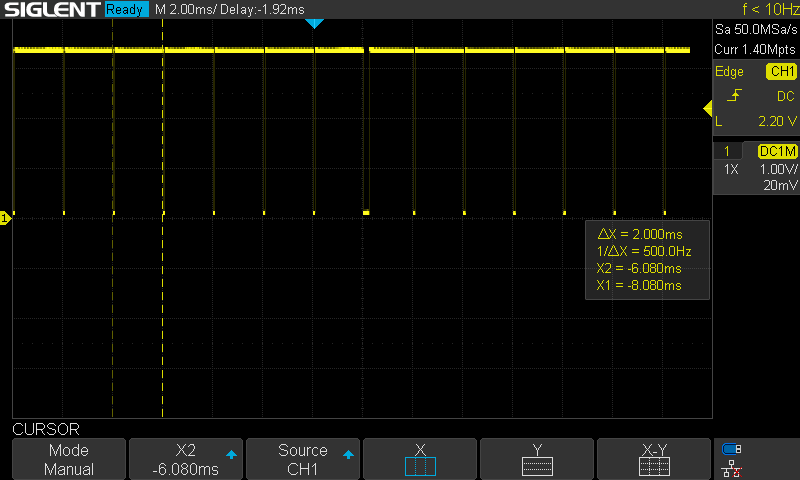
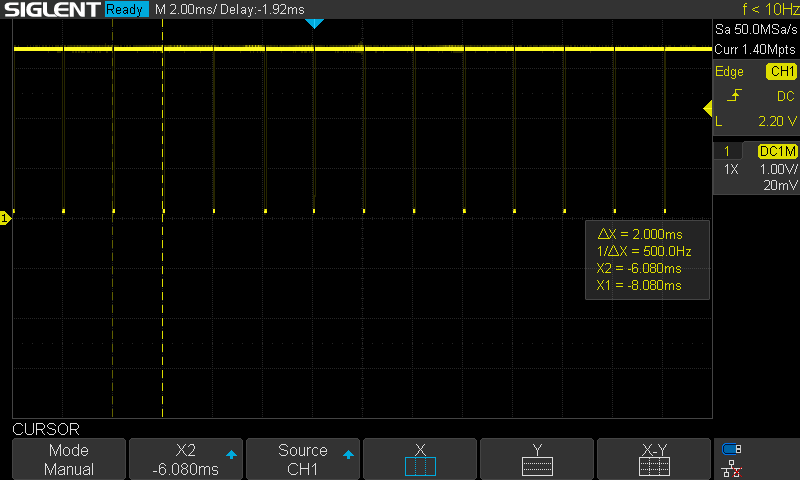
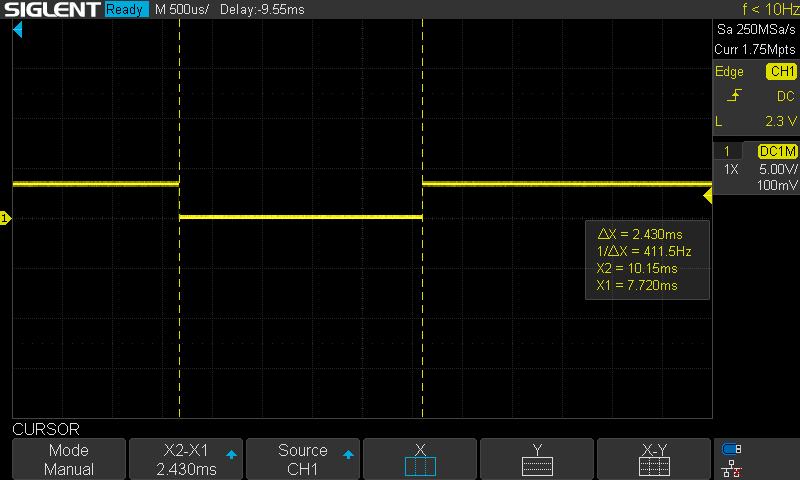
Hardware Timing

The control loop had been set up as a 500Hz FreeRTOS software timer. Although it worked OK for position or speed control, it likely isn't OK for current control. It is not fast enough, and the jitter is quite significant. I therefore set up a hardware timer. As a first test, I set it up to toggle a pin (with some busy delay) on every interrupt. This was quite consistent and accurate, as seen in the next two images.

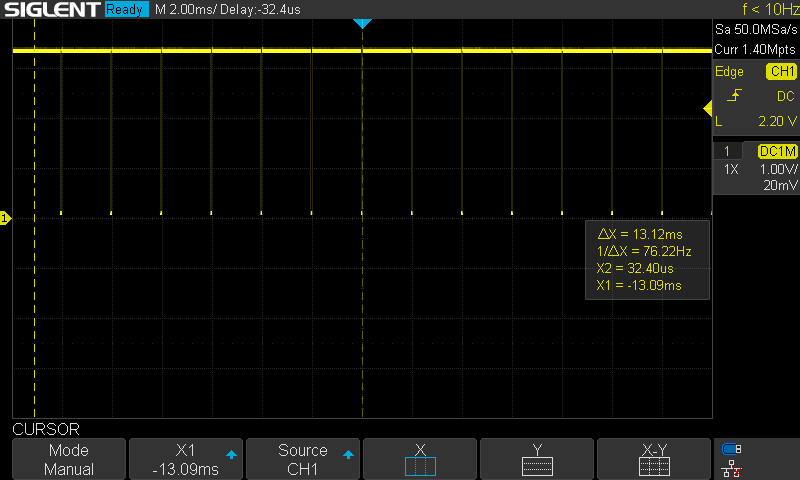
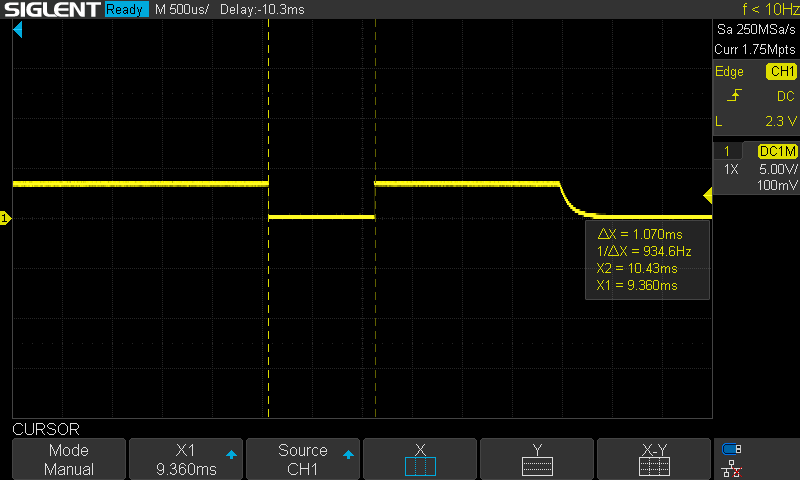
While I could simply run the controller within the ISR, I'd prefer to use that timer to consistently trigger a very high priority task to run the control. I implemented this using a task notification. While it did have a consistent period, I did see the occasional issue as shown at the center of the next image. Sometimes the computation time looked to be noticeably slower.

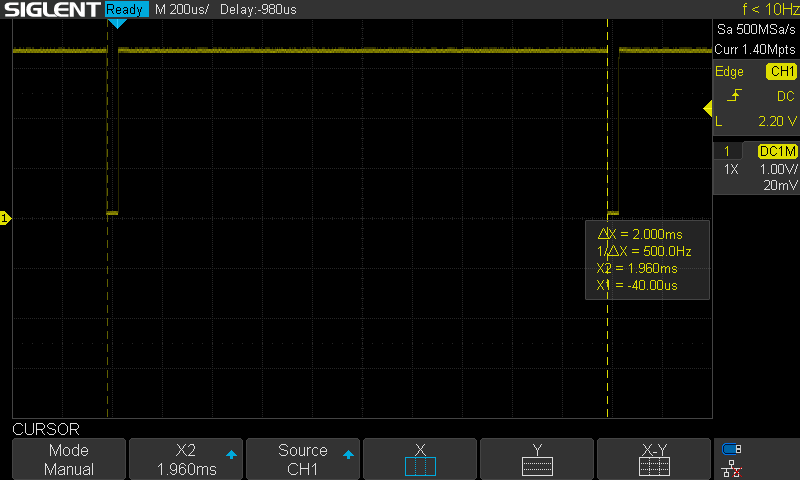
As currently configured, the timer task has higher priority than the control task, so likely that extra computation time is due to a preemption from the timer task. I added a 1ms delay to the primitive and telemetry timers to try to offset those from this timer. This seemed to resolve the issue (at least over short timeframes). In the long term, I need to make the control task higher priority than software timers.

---

VMC Optimizations

The pre-calculations of desired Bezier positions helps not only with position control, but also VMC. The VMC calculations need the current Cartesian position of the foot, and its desired position. This desired position can be and is pre-calculated, but the current position (forward kinematics) and virtual model still need to be calculated online. Looking at this again, I was able to add some optimization. The forward kinematics are as below:

And the Jacobian is defined as:

Therefore, there are some optimizations we can do while calculating the forward kinematics at the same time as the Jacobian.

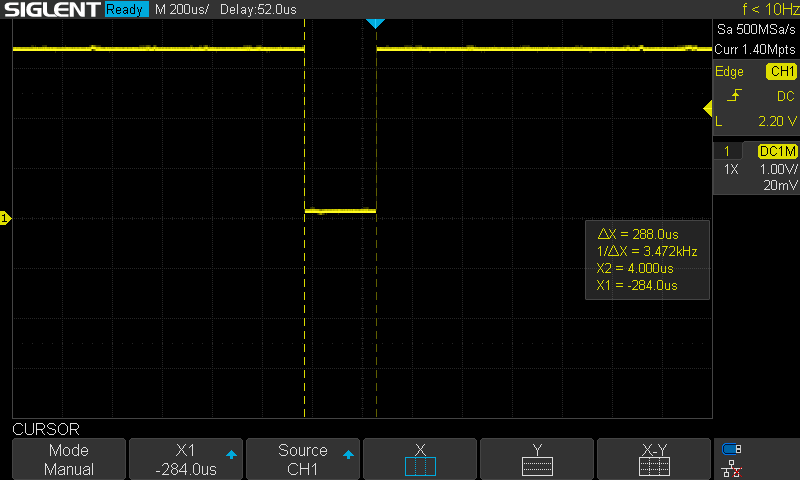
 void calculate_fk_and_jacobian(leg_ik_t * leg, pos_cartesian_t * pos, const pos_joint_space_t joint_angles, jacobian_t * j)
 {
	// Optimization, avoid calculating sin and cos functions twice
	float ct = arm_cos_f32(joint_angles.thigh_angle_rad);
	float st = arm_sin_f32(joint_angles.thigh_angle_rad);
	float ctk = arm_cos_f32(joint_angles.thigh_angle_rad + joint_angles.knee_angle_rad);
	float stk = arm_sin_f32(joint_angles.thigh_angle_rad + joint_angles.knee_angle_rad);

	float temp_0 = leg->calf_length_m * ctk;
	float temp_1 = leg->calf_length_m * stk;

	pos->x = leg->thigh_length_m * ct + temp_0;
	pos->y = leg->thigh_length_m * st + temp_1;

	j->j_01 = -temp_1;
	j->j_00 = -pos->y; // Optimization
	j->j_11 = temp_0;
	j->j_10 = pos->x;
 }

Timing just that function is a bit disappointing though. It takes about 288us. This is a big constraint because I can't get around using Trig functions, and those are already optimized versions. Arm does provide fixed point versions, but it is not clear how I could implement what I need without needing some floating point conversions.

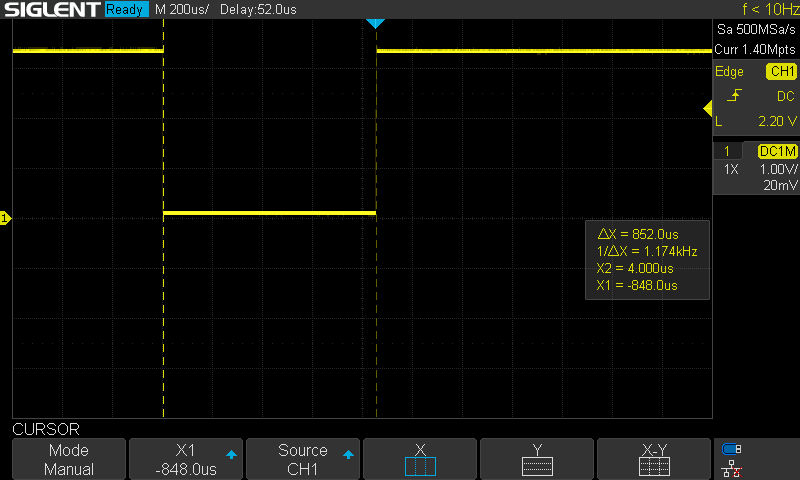
For the entire VMC primitive calculation, the situation is even worse. With damping (and speed estimation) brought back in, this takes about 852us per cycle. That said, that function is currently calculated at 100Hz, so we may be able to go a bit faster.

VMC Tuning

The last log walked through some issues seen with implementing virtual model control on the legs. I spent some more time debugging the issues. The first thing I did was to continue tuning the system. There are a lot of parameters in this system. These are the PID current controller parameters, the VMC effective stiffness and damping, and gain parameters which describe the motor and the mapping from torque to current. I spent time tuning all of these, and was able to get somewhat better results. One major improvement was shifting the current controller from mostly proportional to mostly integral. This is due in part to the single-sided current sensing we have. The current control therefore is somewhat odd and discontinuous.

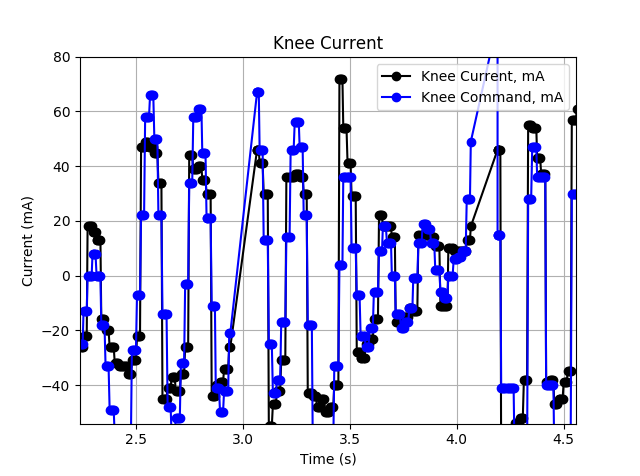
} else if(control_type[i] == CURRENT || control_type[i] == PROPRIOCEPTIVE_PRIMITIVE)
		{
			if(motors[i].current_ma_setpoint >= 0)
			{
				float cmd = calculate_pid(&cur_params[i], motors[i].current_ma_setpoint, motors[i].current_mA);
				// Only allow forward drive
				if(cmd > 0)
				{
					tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 1 : 0, 0);
					tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 0 : 1, (int32_t) cmd);
				}
				else
				{
					tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 0 : 1, 0);
					tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 1 : 0, 0);
				}
			}
			else
			{
				// Flip direction of control and direction of setpoint
				float cmd = calculate_pid(&cur_params[i], -motors[i].current_ma_setpoint, motors[i].current_mA);
				// Only allow reverse drive
				if(cmd < 0)
				{
					tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 1 : 0, 0);
					tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 0 : 1, 0);
				}
				else
				{
					tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 0 : 1, 0);
					tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 1 : 0, (int32_t) cmd);
				}
			}
		}

 If a proportional controller commands driving in the opposite direction of what I know the current should be, I don't command negative. Instead I drop to 0 command. In the next control loop, we then expect the current to shift towards zero, and the controller kicks back on. This inherently means even in a perfect world a proportional controller would bounce around the desired current. However, an integral controller has some inertia to it and would be expected to bounce around less. In testing, this does seem to work. The image below shows the current controlling on one example. The command is oscillatory due to the VMC tuning, but the current tracking looks pretty good.

 The image below shows the (unloaded) proprioceptive control that I achieved. However, when I tried to have all four legs use this controller to walk, it doesn't work well. The proprioceptive control is just not ready. I therefore dug deeper into the potential issues.

The motor controllers use a ATSAMD21 Cortex M0+ running at 48MHz. This is a decent microcontroller, but critically it does not have an FPU. Some benchmarks with the same CPU show that floating point multiplication requires ~16.5X the time of integer multiplication, and floating point division is ~14X slower than integer division. Note that the exact timing does depend on the exact data and optimizations, but nonetheless it is clear that floating point math is much slower than integer math. I knew this of course, but many of the calculations including PID, inverse and forward kinematics, and VMC are far easier to do in floating point than fixed point. It is much harder to make a mistake during development, and I hadn't run into any issues.

In addition, I am running FreeRTOS on the SAMD21. The control loop, motion primitive (and VMC) calculations, and telemetry all are software timers. The control loop is 500Hz, and the motion primitive and telemetry are each 100Hz. Again, running control loops in software timers is not ideal, but I didn't have issues with position or velocity control. However, current control in most commercial systems is the fastest of the control loops. In fact, it was implemented in analog for most systems until fairly recently. With VMC, we have the extra challenge that the current setpoint must be updated at every re-calculation of the motion primitive. If this is not done often enough, the tracking will be poor. I had previously simply attempted to run the motion primitive calculations at 200Hz, but the system malfunctioned. It was not clear at the time what happened, but this implied I am running into computational issues.

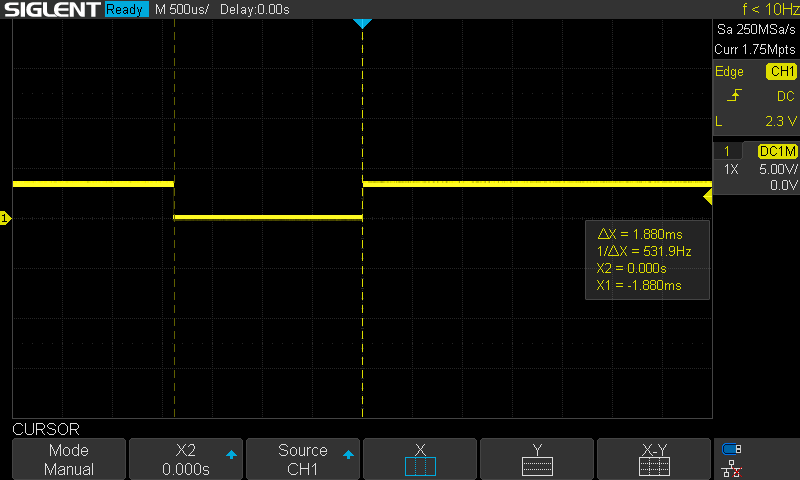
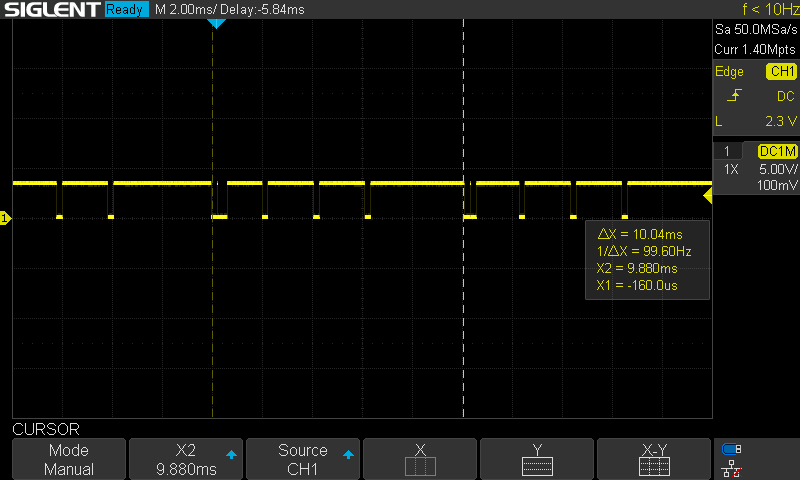
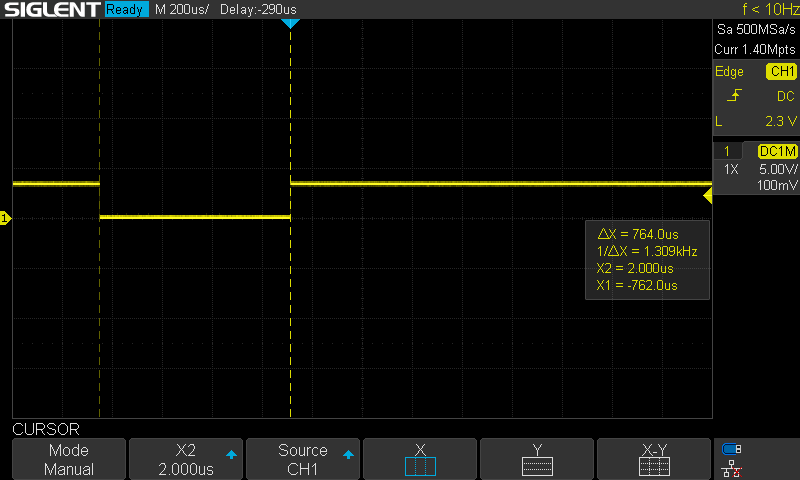
To look into computational issues, I set up an external pin to toggle low then high, wrapped around code of interest. I can then look at the signal on my oscilloscope to see how long sections of code are taking. The first one I looked at was the motion primitives software timer callback. This section has varying computation time since it supports linear or quadratic Bezier curves (which are not calculated in constant time), and both position and VMC tracking. For this profiling, I was running quadratic Bezier curves with VMC tracking. As seen in the image below, this calculation took about 1.88ms.

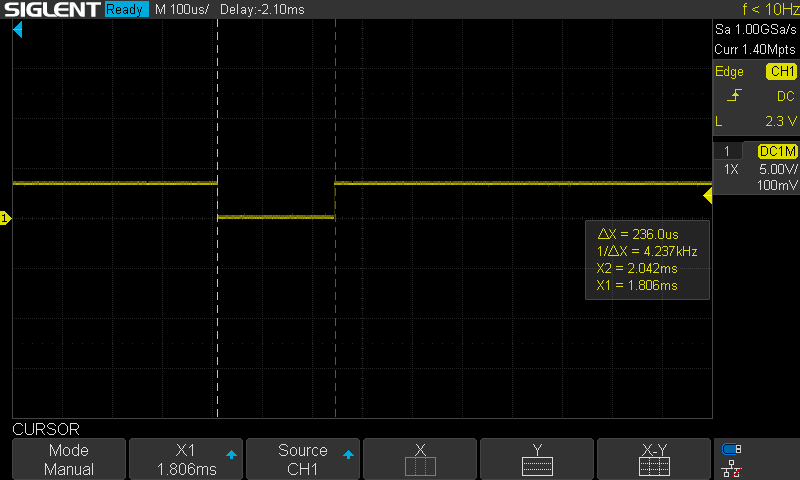
I then looked at my control loop. Again, this is not constant time. Here, we are in VMC current control mode. This was much faster than the motion primitive callback, only requiring 236us.

More telling was the timing consistency of the control loop. At 100Hz there is clear lag in the calculations, and two control loop cycles are bunched together. This 100Hz matches up to the rate of the motion primitive calculations, and since that can require almost 2ms (the period of the control loop), this is likely interfering with the control loop.

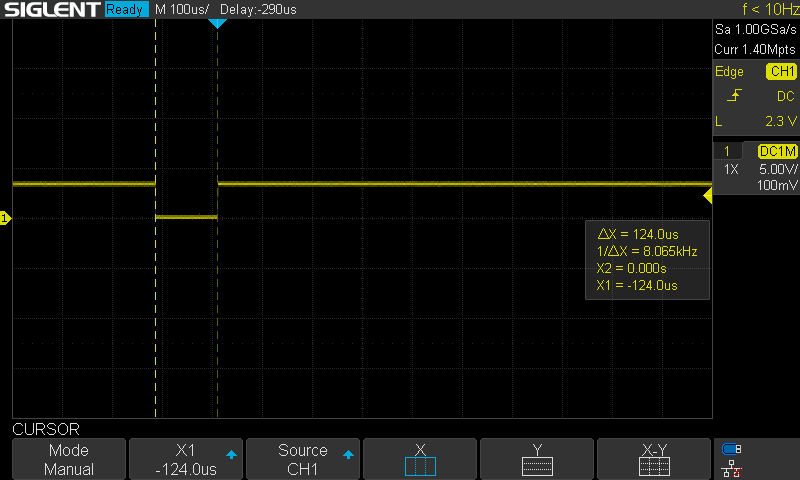
To complete the initial measurements, I also profiled the time required to add the telemetry CAN messages to their queue. That only required 124us, and is unlikely to be an issue.

So, we know the motion primitives timer callback is too slow. The first step to improving its speed is to better understand where the slowdown is. That timer callback performs two main steps. First, it calculates the desired Cartesian foot position via a quadratic Bezier curve. Then, it calculates the VMC. I wrapped only the VMC calculations, and that section required about 1.56ms. Therefore, it is the clear initial focus. My first suspicion was the trig functions needed for the forward kinematics and the Jacobian calculation. I had been using the arm_sin_f32 and arm_cos_f32 functions within the forward kinematics, but I changed back to standard sin and cos from math.h. With only 4 trig function calls changed from Arm's versions to the math library, the time increased up to 2.43ms.

Clearly, we should use Arm's faster trig calculations. I also noticed that my Jacobian calculation was using sin and cos. Further, those calculations were identical to those performed within the forward kinematics. I therefore created a single function that also calculated the Jacobian.

 void calculate_fk_and_jacobian(leg_ik_t * leg, pos_cartesian_t * pos, const pos_joint_space_t joint_angles, jacobian_t * j)
 {
	// Optimization, avoid calculating sin and cos functions twice
	float ct = arm_cos_f32(joint_angles.thigh_angle_rad);
	float st = arm_sin_f32(joint_angles.thigh_angle_rad);
	float ctk = arm_cos_f32(joint_angles.thigh_angle_rad + joint_angles.knee_angle_rad);
	float stk = arm_sin_f32(joint_angles.thigh_angle_rad + joint_angles.knee_angle_rad);

	pos->x = leg->thigh_length_m * ct + leg->calf_length_m * ctk;
	pos->y = leg->thigh_length_m * st + leg->calf_length_m * stk;

	j->j_01 = -leg->calf_length_m * stk;
	j->j_00 = -leg->thigh_length_m * ct + j->j_01;
	j->j_11 = leg->calf_length_m * ctk;
	j->j_10 = leg->thigh_length_m * ct + j->j_11;
 }

I also did some more minor optimizations, like pre-calculating the inverse of the gear ratio so that a floating point multiply is used instead of a division. These combined brought the time down significantly, to about 1ms.

Finally, there is one section that calculates the foot's Cartesian speed using a difference and low pass filter within the virtual model controller. This is required to calculate damping. However, as a test I commented that out. Now the total time dropped to about 0.764ms.

So, without any operational changes, we can get the time down to about 1ms and with some code removal (that could be replaced in integer math) down to 0.764ms. While this helps, it is unlikely to allow significant loop speed increases. Therefore, I think to get better VMC performance, we need to go faster. For this there are a few options that I am looking into in parallel:

• Set up current controller to be only integer math
• Setup control loop on hardware timer
  • Or hardware timer triggering super high priority task to take over
• Shift parts or all of motion primitive calculations to integer math
• Design and build new version with FPU (I am doing another unrelated board with a 168MHz STM32F4 with FPU as my first experimentation with the STM32 line)

In the last log for the motor controllers used on this robot, I discussed how the motion primitives were updated to roughly match the gait of the MIT Cheetah according to the following video:

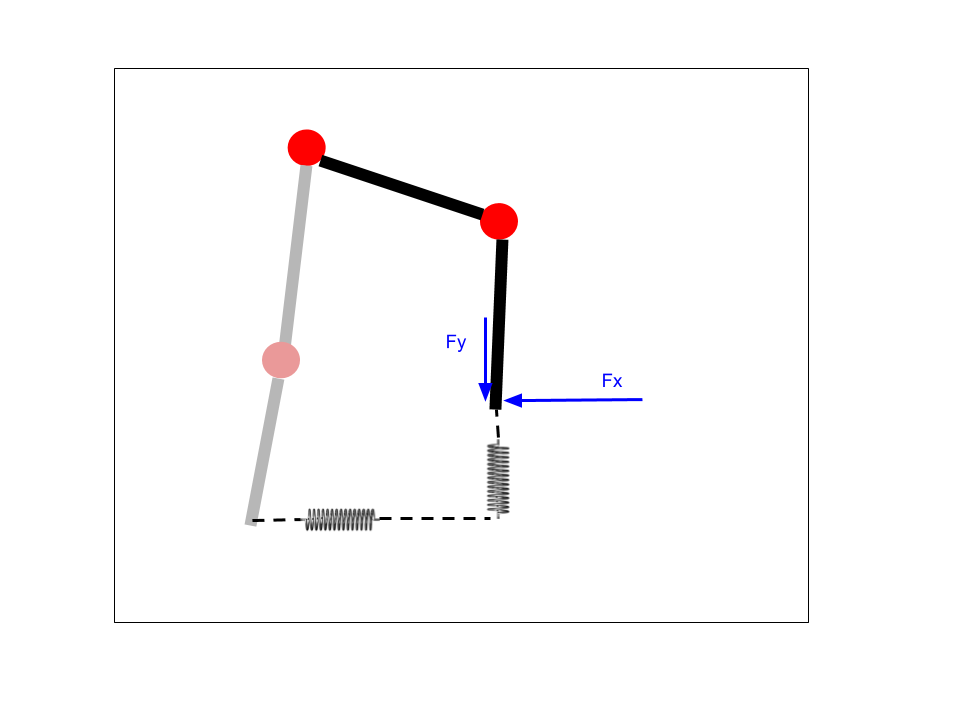
I also noted that my implementation was pretty far from how the MIT Cheetah does its leg motion control. It was different in at least two critical ways. First, while I had 3-4 points in my profiles, and the leg would track between these points according to linear interpolation, the Cheetah uses Bezier curves for smoother motion (or it did at one time per this paper). Second, while my robot tracked those profiles simply using inverse kinematics and position control, the Cheetah is more advanced. Series-elastic actuators have a long history in robotics in helping to stabilize walking motion. The Cheetah uses virtual model control to simulate elasticity in its motion. In the simplest representation of this, consider the image below. Instead of driving the leg to a given position, we instead create a virtual spring (and damper) between a desired point and the foot. The forces that would occur due to this virtual model are calculated, and we drive the hip and knee motors in current, or torque, control mode to achieve this force. Therefore we can think of the foot as being dragged around in space by a virtual spring and damper. Instead of punching the ground with position control, a virtual model controlled leg impacts the ground as if there was an inline spring, and the motion is therefore much smoother. With its high-performance, low gear-ratio brushless motors, the Cheetah is great at doing this. I am using 150:1 gear ratio <$10 brushed motors with single-sided current sensing. Therefore I do not expect nearly as good performance, but I still want to do as best as possible.

Bezier Motion Profiles

Bezier curves are parametric curves defined by a few control points. Various order Bezier curves exist, and in fact linear Bezier curves are simply linear interpolation. Therefore technically I was already using Bezier curves. But clearly motion like that shown below is not smooth.

And I do mean smooth in the mathematical sense. The derivative of the curve is discontinuous, which can make for jumpy motion. To keep things a bit simpler, I focused on using quadratic Bezier curves. These also do not ensure mathematically smooth profiles, but by tuning the shape, I can get much smoother motion. In the implementation, we must always have an even number of control points. All even indices (starting at 0) are points that the motion moves through. All of the odd index points "pull" the profile to shape it. Wikipedia has a good explanation on how to generate a quadratic Bezier curve. With this implemented, I regenerated the profile above, but with quadratic Bezier curves and some shaping points. For sanity, I also rotated things so that the leg "down" is down also.

Clearly, this motion will be much smoother and hopefully will result in less jerky walking.

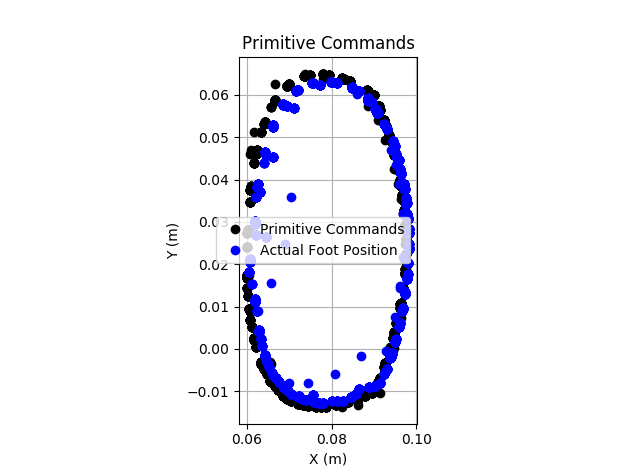
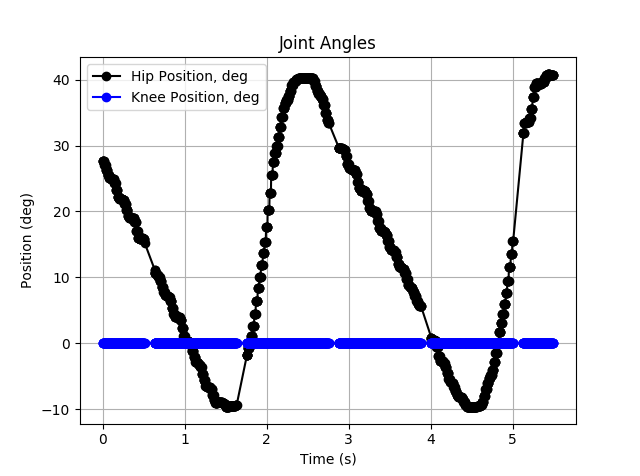
I tested this with position control (virtual model control will be discussed later), and it was successful. This is real test data, with a 2s period. The actual foot positions lag somewhat, but the tracking is overall quite decent.

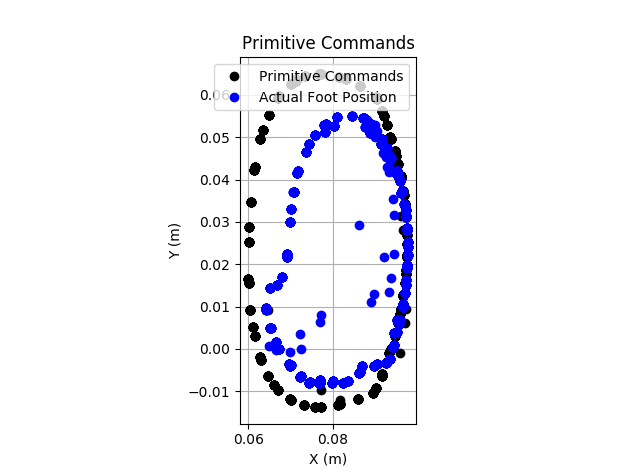
If we speed up the cycle, it is clear that the motors cannot keep up. At this point it isn't clear if this is a PID tuning issue, or a hardware limitation. This example has a 750ms period, so more than twice as fast.

Virtual Model Control

In one of the logs for the motor controller, I had talked about current control and virtual model control, but did not get great results. I revisited this again, now that I have motion primitives working. I would like to use the Bezier curves along with virtual model control. There are a number of challenges here:

• Depending on the leg orientation, it may not be mathematically possible to generate the desired virtual force front joint torques (think about your leg held out straight with locked knee, now push down...)
• We only have single-sided current sensing, but we want to control current in both directions. This requires care in implementation.
• The motion profiles must be calculated faster than they did for positional control. The motion profile calculations are needed for the current calculations. This was done at 20Hz previously, but that is not fast enough to re-calculate current commands appropriately

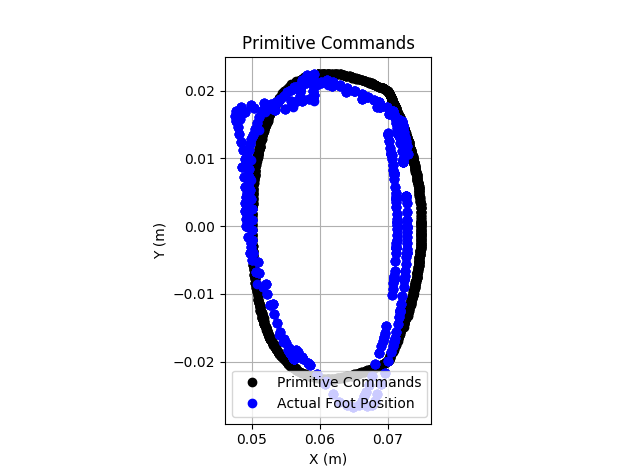
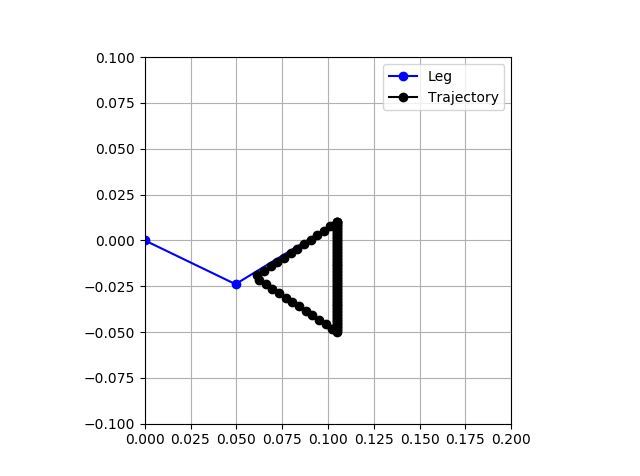
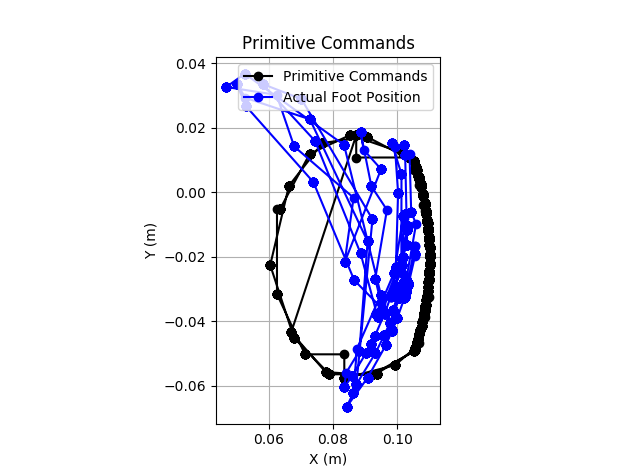
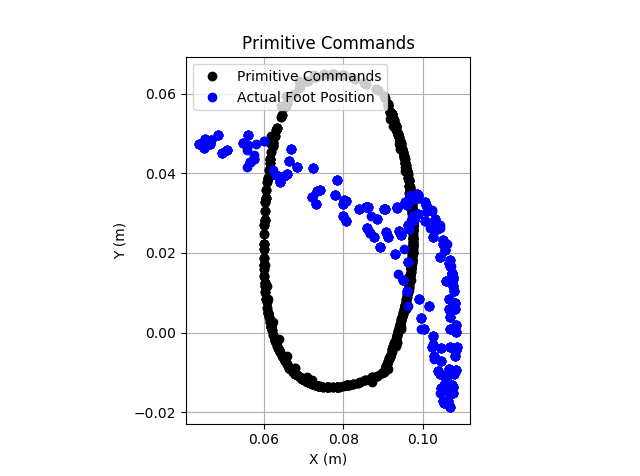
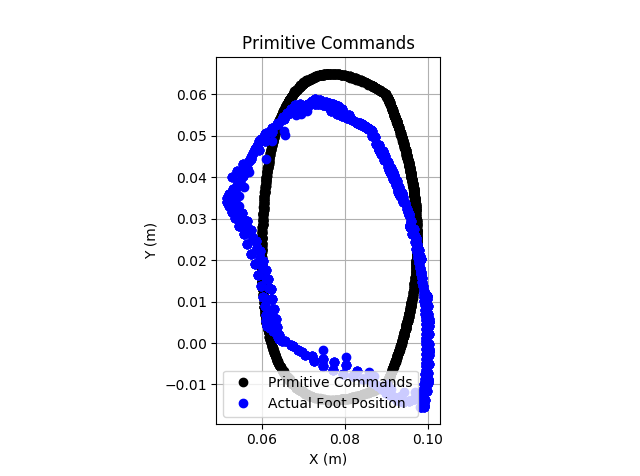
During some of the initial testing, the performance was poor. The image below shows the commanded position per the Bezier curve in black, and the actual foot positions in blue. Clearly it is not tracking well.

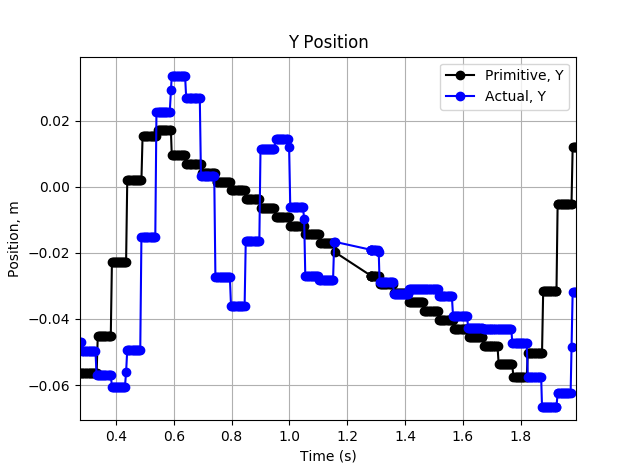
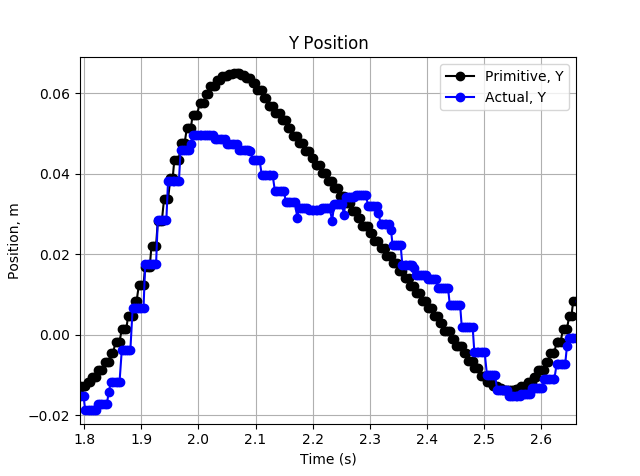
However, there are some promising signs. It is difficult to tell in the image above, but the positional tracking is actually __somewhat__ working. The image below shows the Y-axis tracking over a single cycle. There is clear damped oscillation about and tracking of the desired Y position profile.

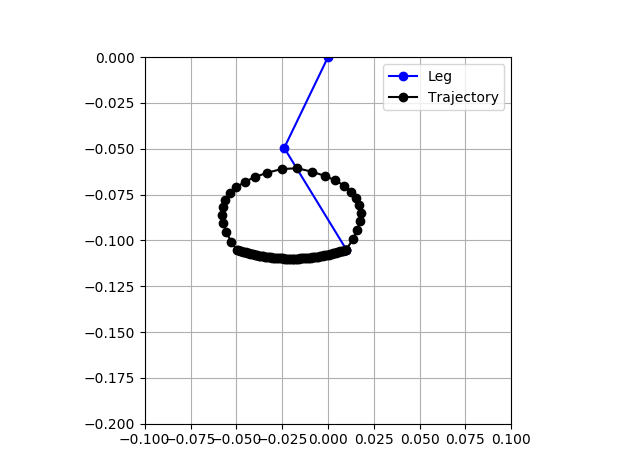
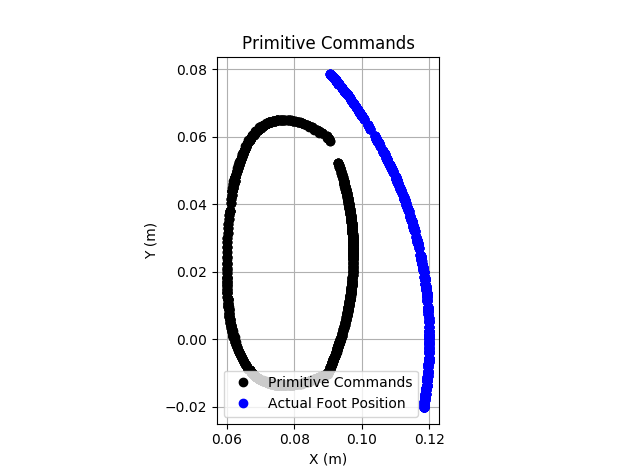
At this point, the primitives calculations were still at 20Hz. After increasing that rate to 100Hz, tuning the virtual model, motor model, current PID loops, and more, I was making progress, but results were still a bit odd. The image below shows a typical response. The actual foot position looks more like a banana than the proper Bezier curve.

The tracking on the Y-axis actually wasn't too bad here, although there is a strange dip near the peak.

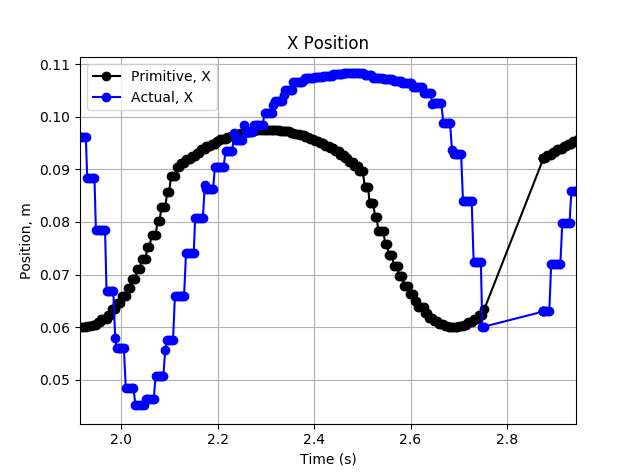
The X-axis tracking however, is quite poor. There is significant lag, overshoot, and undershoot. This is the main cause for the poor tracking.

Thinking about this further, one cause is the limited controllability in the "X" direction. While movement of the hip alone can control Y fairly well, X motion in this range requires synchronized motion of both motors. More importantly, through some of this region the leg is nearly straight out, which gives very little control authority for pushing outwards. As an extreme example, consider the following. In this case, only the hip motor moved and the knee was straight. It is clear that near the front of the desired profile, the leg is nearly straight.

Some of the tracking issues also seemed to be temporal, that they cannot keep up with the speeds. I therefore ran a test with a 3s period to show how the control is working. In this case, the virtual model control actually works decently well. Although the actual shape doesn't match perfectly, it is clearly better than previous attempts.

That is where is stands for now. I believe there are a few things I can do to improve this:

• Stiffen up VMC and current controller to track motion faster
• Generate new motion profiles that provide better conditioning for VMC