Justificación:

Se tenía la opción de realizar un robot hexápodo o un cuadrúpedo. Nos decidimos en trabajar con un robot cuadrúpedo para poder reducir costos en cuanto a la compra de sevomotores y uso de material, ya que se tiene planeada la construcción física de este robot.

En cuanto al diseño de 4 patas, se investigaron las opciones de un robot inspirado en mamíferos y de uno inspirado en arácnidos. Decidimos optar por el diseño de arácnidos ya que este puede obtener una buena estabilidad con una menor cantidad de servomotores. El diseño que se presenta en este proyecto presenta únicamente 2 servomotores por pata, lo cual en el caso de un diseño inspirado en mamíferos no otorgaba una buena estabilidad ni un movimiento más bioinspirado, sino que en ese caso era necesario de al menos 3 servomotores por pata.

Nos inspiramos en el diseño del video que se muestra a continuación. Adicionalmente se logró verificar un correcto funcionamiento de las patas con 2 grados de libertad (2 servomotores).

Partiendo de esta idea, se realizaron ciertos bocetos, principalmente para el diseño de la pata. En estos se ve que se mantiene el motor encargado de la rotación sobre el eje vertical en la misma posición. Por otra parte se cambió un poco la idea de funcionamiento del motor que se encarga de levantar la pata, inicialmente la pata iba a ser completamente una pieza recta y por debajo del motor de rotación, donde la salida del motor iba a estar anclada al robot y el movimiento sería mediante al cuerpo de servomotor. Esto se muestra en los siguientes bocetos:

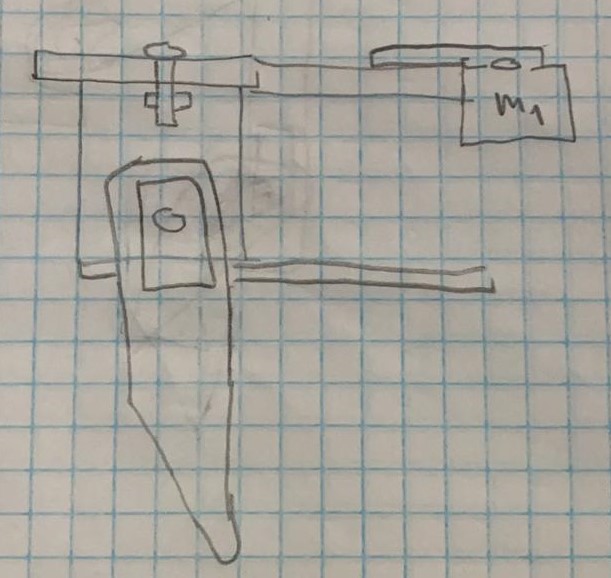
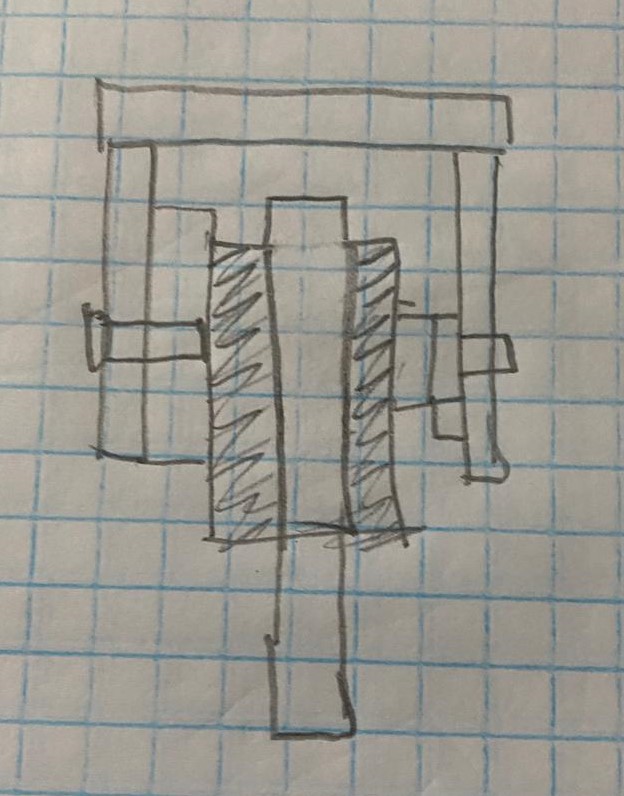
Eventualmente decidimos cambiar la forma de la pata, para otorgarle un movimiento más bioinspirado y también decidimos mover la posición del motor encargado de levantar la pata por encima del motor encargado de la rotación, esto con el objetivo de reducir el momento de inercia de la pata, lo cual facilitará su giro.

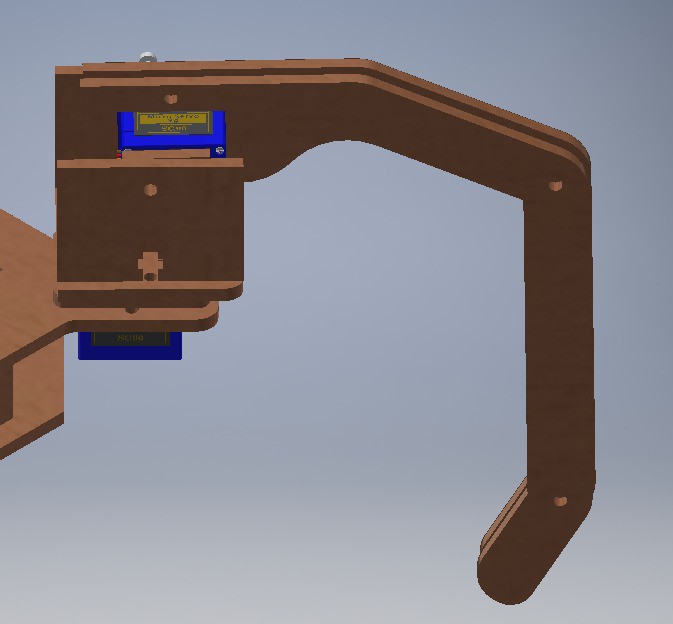
Validación de la selección de motores:

Se escogieron los servomotores micro-servo SG90, los cuales poseen un torque máximo de 2.2 kgf-cm. Se plantearon 3 casos críticos para analizar el robot y corroborar que los motores son capaces de soportar los movimientos deseados.  Se espera tener un factor de seguridad de al menos 3 para garantizar un movimiento fluido.

El primer caso corresponde al movimiento de levantar una las patas. El motor debe ser capaz de igualar el torque provocado por el peso. Para ello se calculó el centro de masa de la pieza, por medio de el software Autodesk Inventor, y se utilizó la densidad promedio del MDF de 700 kg/m^3. El resultado indicó que se tiene un factor de seguridad de 45, lo cual indica que este motor cumple satisfactoriamente su función de levantar la pata.

El segundo caso corresponde a hacer rotar todo el ensamble de la pata. En este caso la gravedad no tiene efecto ya que la rotación ocurre en un plano perpendicular a esta. Se calculó la aceleración angular máxima que podría generar el motor al sistema y se analizó si esta es suficiente para el movimiento deseado. Para ello se calculó nuevamente mediante a Inventor el momento de inercia (también se aplicó el teorema de ejes paralelos para obtener la inercia sobre el eje de rotación de la pieza) y se empleó la segunda ley de Newton rotacional. El resultado indica una aceleración máxima del sistema de 3,543 rad/s^2. Esto suena un dato exageradamente alto, sin embargo esto se debe a la baja inercia de la pieza.

El tercer, y último caso, corresponde al torque necesario en los motores para sostener todo el peso de el robot cuando se encuentra en 3 patas. Para ello se sabe que la fuerza normal ejerce un torque sobre las patas, y ya que el robot es simétrico se aproximó a que esta corresponde a 1/3 del peso de todo el robot. También se consideró un peso de 50 g correspondiente a la batería que se utilizará para alimentar al Arduino. En este último caso se obtuvo un factor de seguridad de 3.17, lo cual se encuentra todavía por encima del valor mínimo establecido de 3. 

En la sección de archivos se adjunta un Excel con los cálculos mencionados anteriormente.

Selección de componentes

Son tres los módulos donde es necesario seleccionar los componentes más eficientes que cumplan con las características requeridas: suministro de potencia, tipo de comunicación y controlador. La selección de componentes se realizó por medio de la herramienta trade study.

1. Suministro de potencia

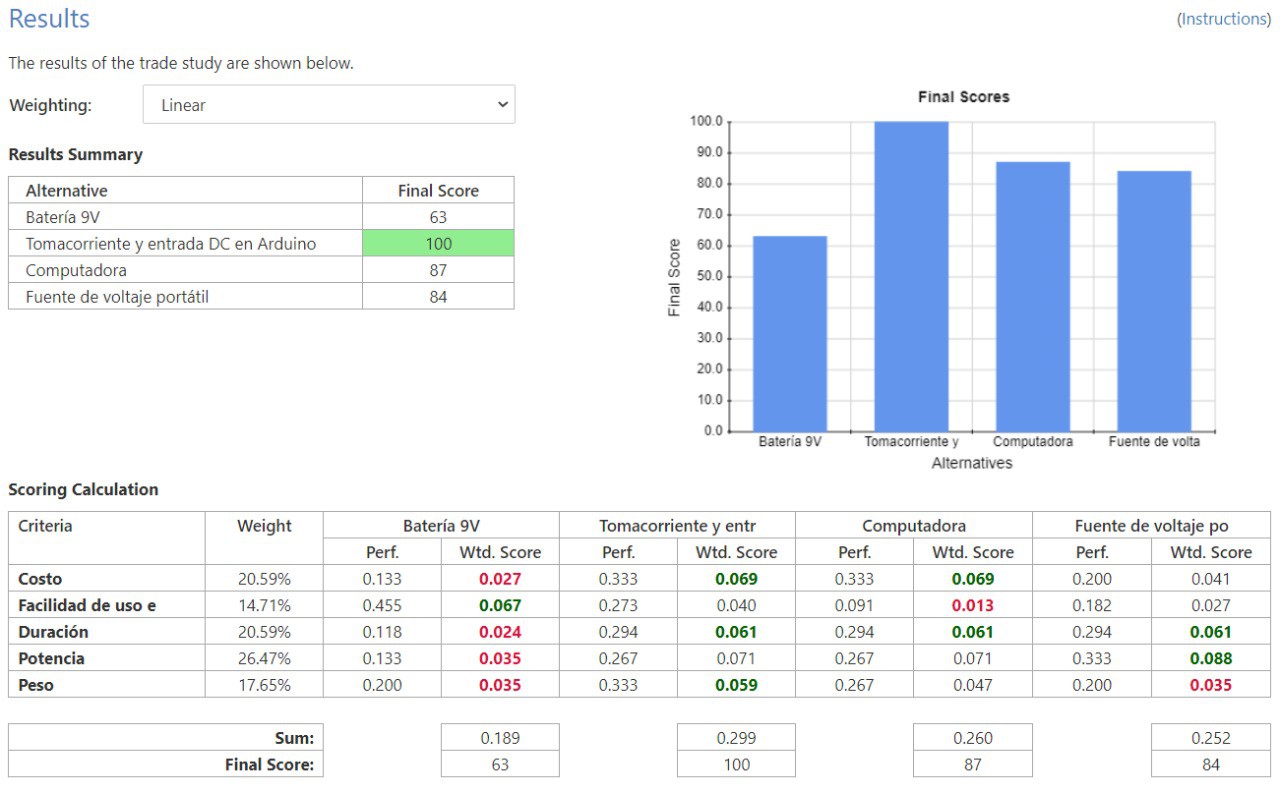
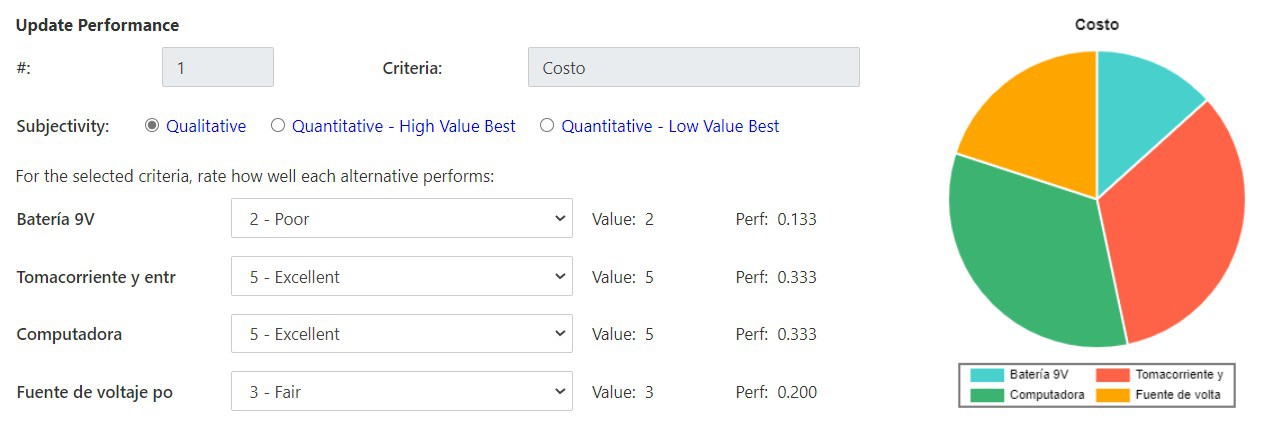
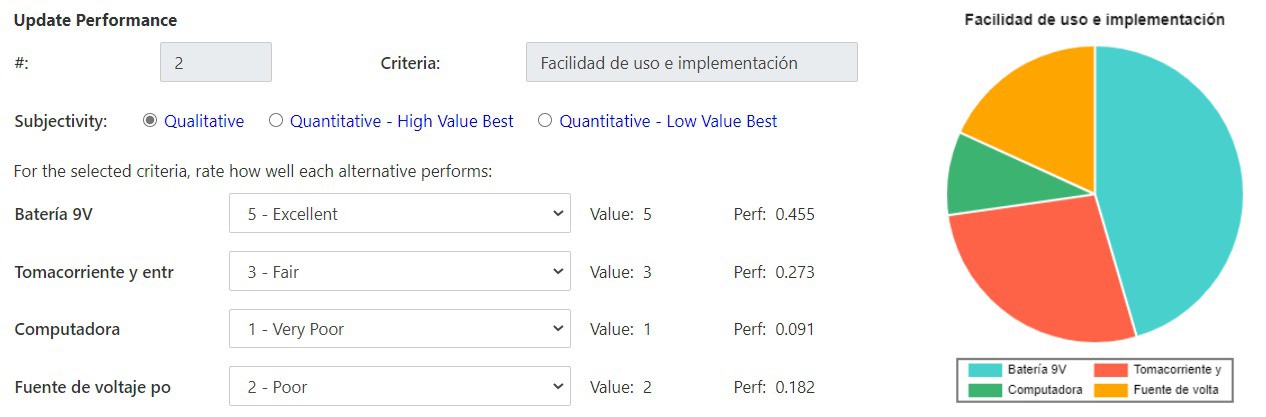
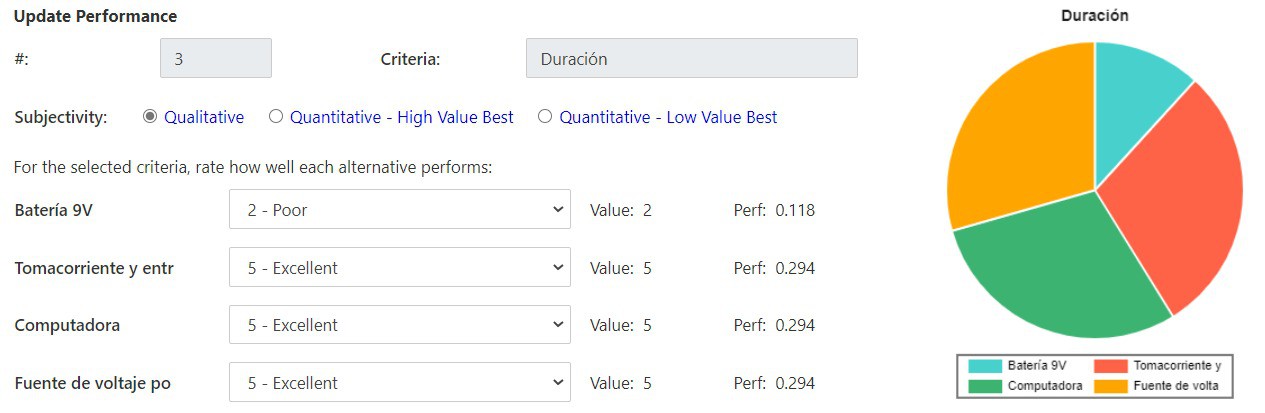
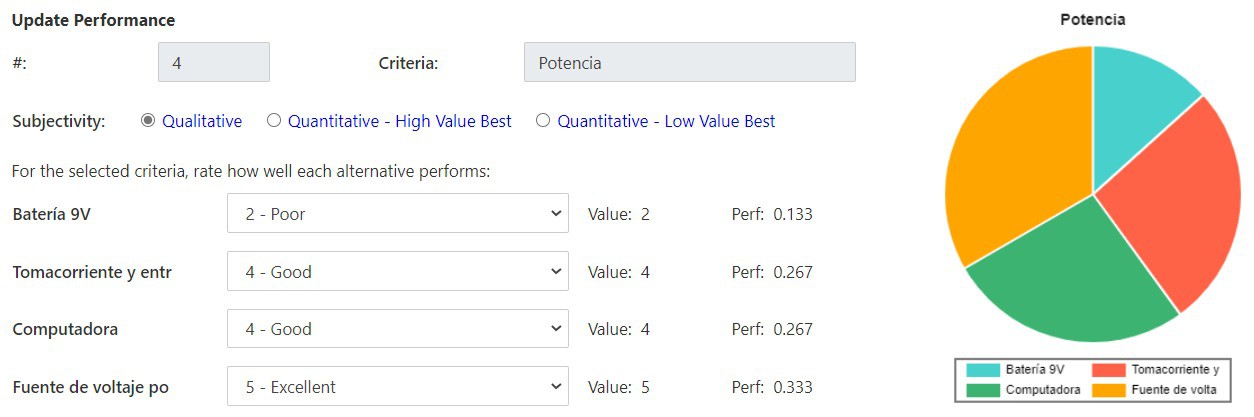
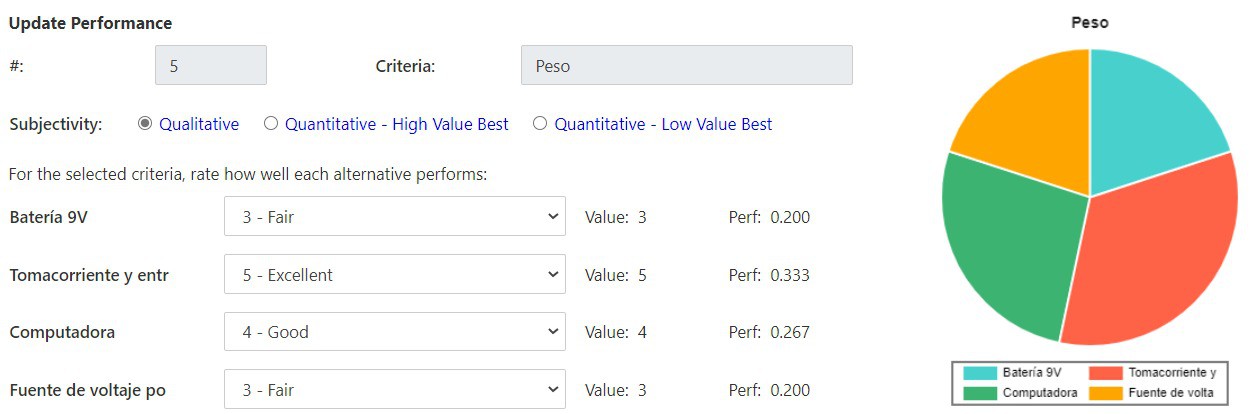
Las opciones consideradas fueron una batería de 9V, conexión a tomacorriente a entrada DC del Arduino, puerto USB de la computador y una fuente de voltaje portátil (módulo MB102). Fueron tomadas estas opciones debido a factores como accesibilidad en el mercado y bajo costo. El criterio que más peso se le asigno fue la potencia suministrada ya que esta puede llegar a quemar la placa o los servomotores en caso fuera incorrecta. Los siguientes criterios con mayor peso son el costo y la duración, esto debido a que se tiene un presupuesto limitado para la realización del proyecto y se solicito una operación continúa del robot de al menos 30 minutos.  Seguido viene el criterio del peso ya que este es un factor relevante para los cálculos de torque y movimiento continuo del cuadrúpedo. Por último se tiene el criterio de facilidad de uso e implementación ya que no es algo que llegue a afectar directamente el correcto funcionamiento del sistema. Con estos criterios y pesos asignados a cada uno, se llega a la conclusión que la mejor opción es la conexión de tomacorriente a entrada DC del Arduino. 

Criterios de selección:

2. Controlador

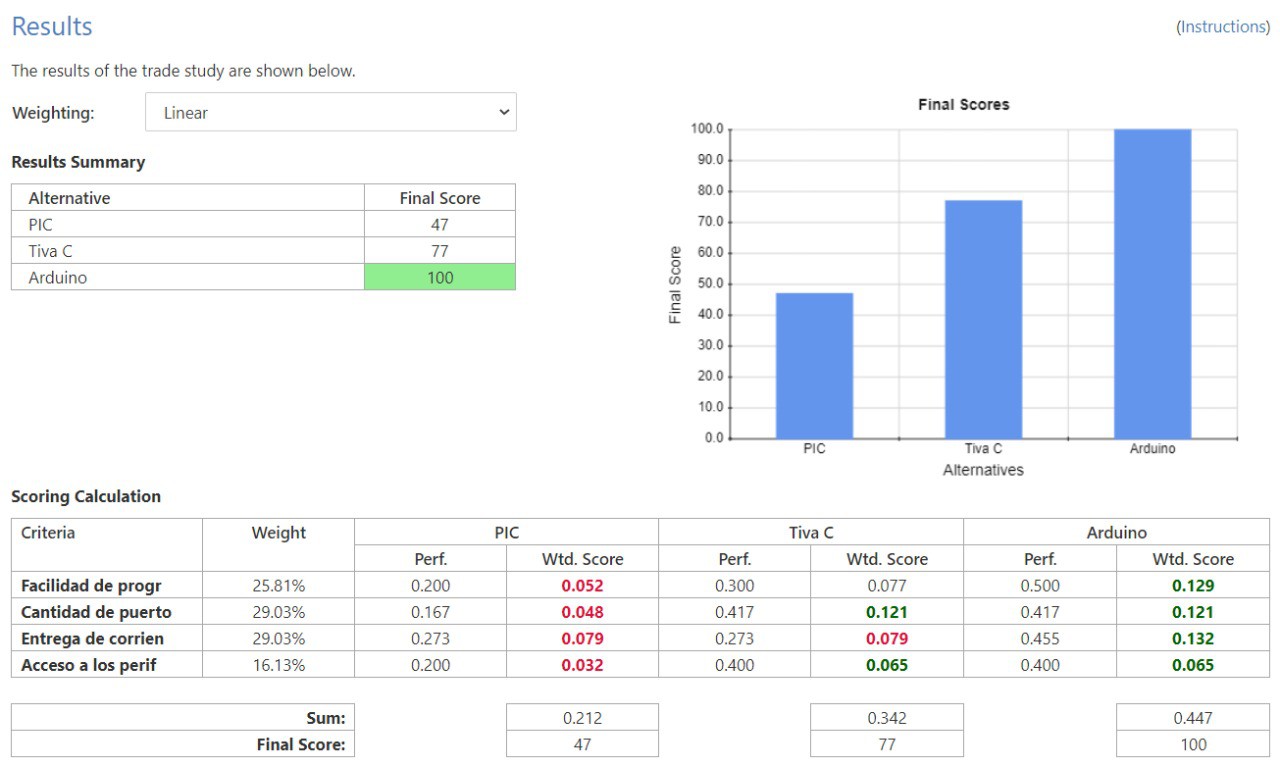
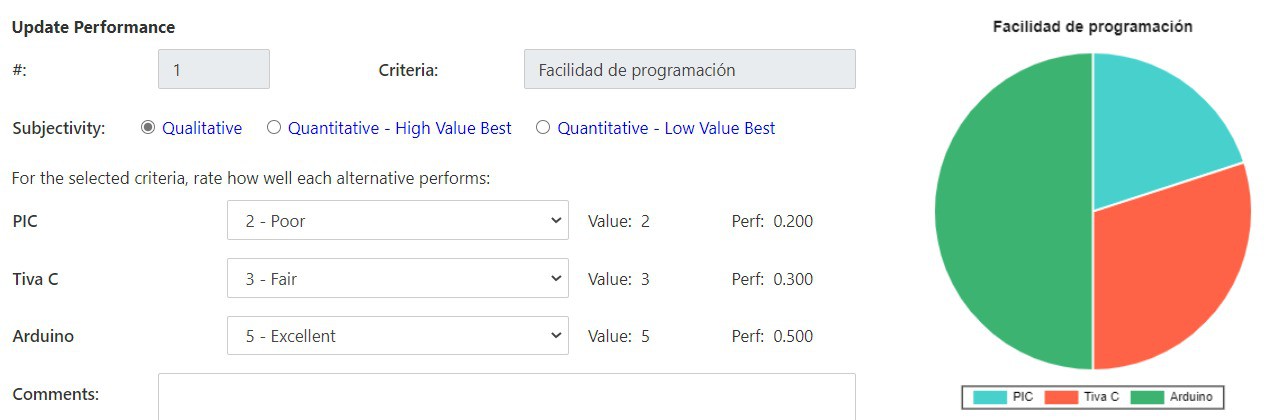
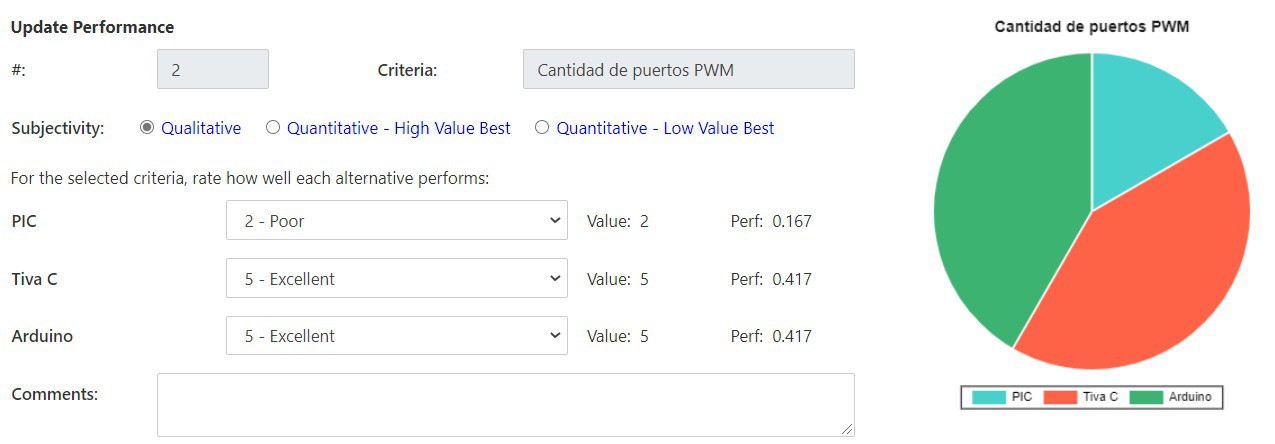
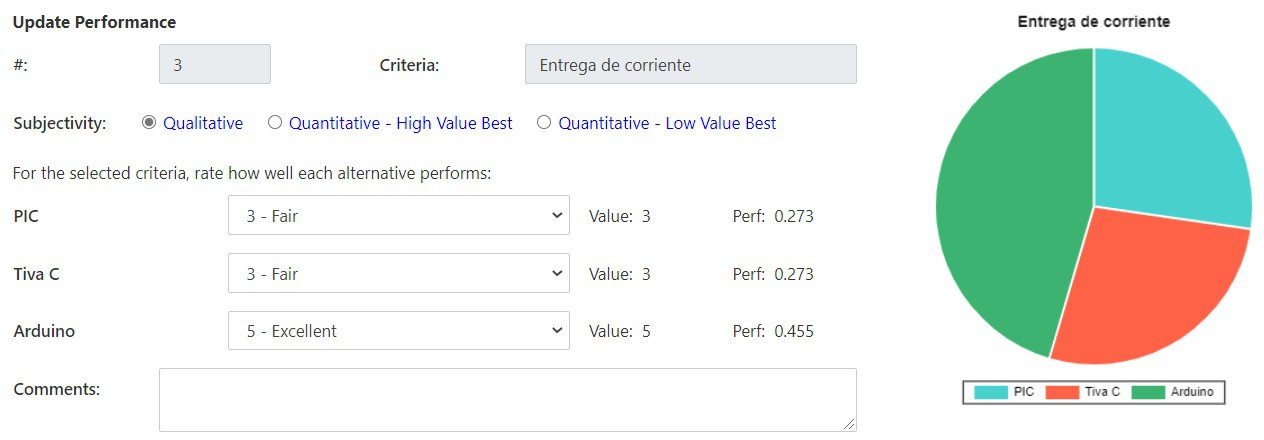
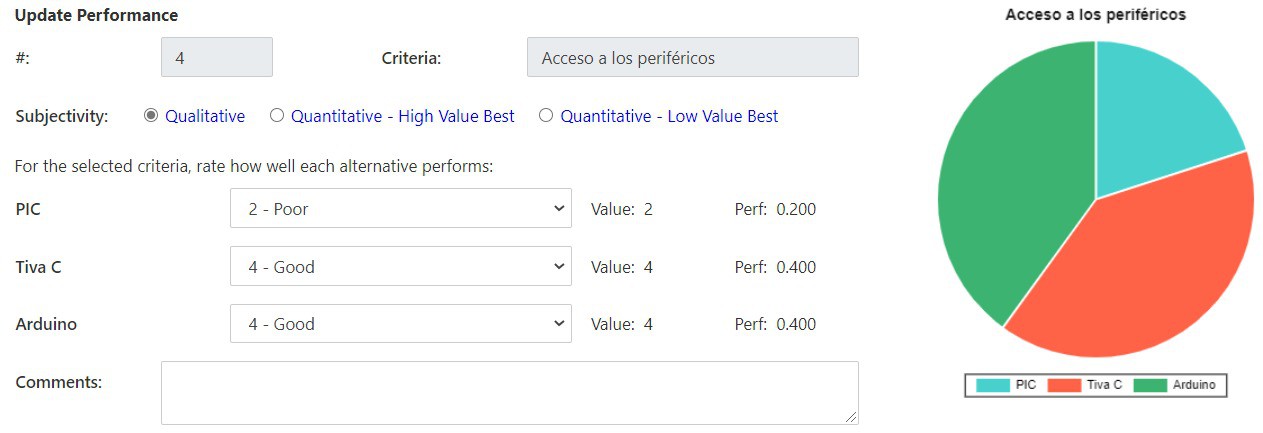
Para el caso del controlador las opciones consideradas fueron un PIC16F887,  Tiva C series TM4C123G y el Arduino UNO R3. Fueron tomadas estas opciones debido a que el equipo de trabajo ya contaba con estos controladores previo a empezar este proyecto y así obtener una reducción en los costos. Al mismo tiempo ya se contaba con el conocimiento para la programación de estos controladores. Los criterios que se les otorgaron un mayor peso fueron la cantidad de puertos PWM disponibles y la entrega de corriente de la placa. La cantidad de puertos PWM es vital para lograr controlar los ocho servomotores a utilizar y la entrega de corriente es igual de importante para obtener un correcto funcionamiento de todo el sistema. El siguiente criterio con mayor peso es la facilidad de programación, esto debido a que el equipo desea programar en un lenguaje de alto nivel para evitar complicaciones. Por último se tiene el criterio de acceso a los periféricos debido a que no es algo que llegue a afectar directamente el correcto funcionamiento del sistema. Con estos criterios y pesos asignados a cada uno, se llega a la conclusión que la mejor opción de controlador es el Arduino UNO R3.

Criterios de selección:

3. Comunicación

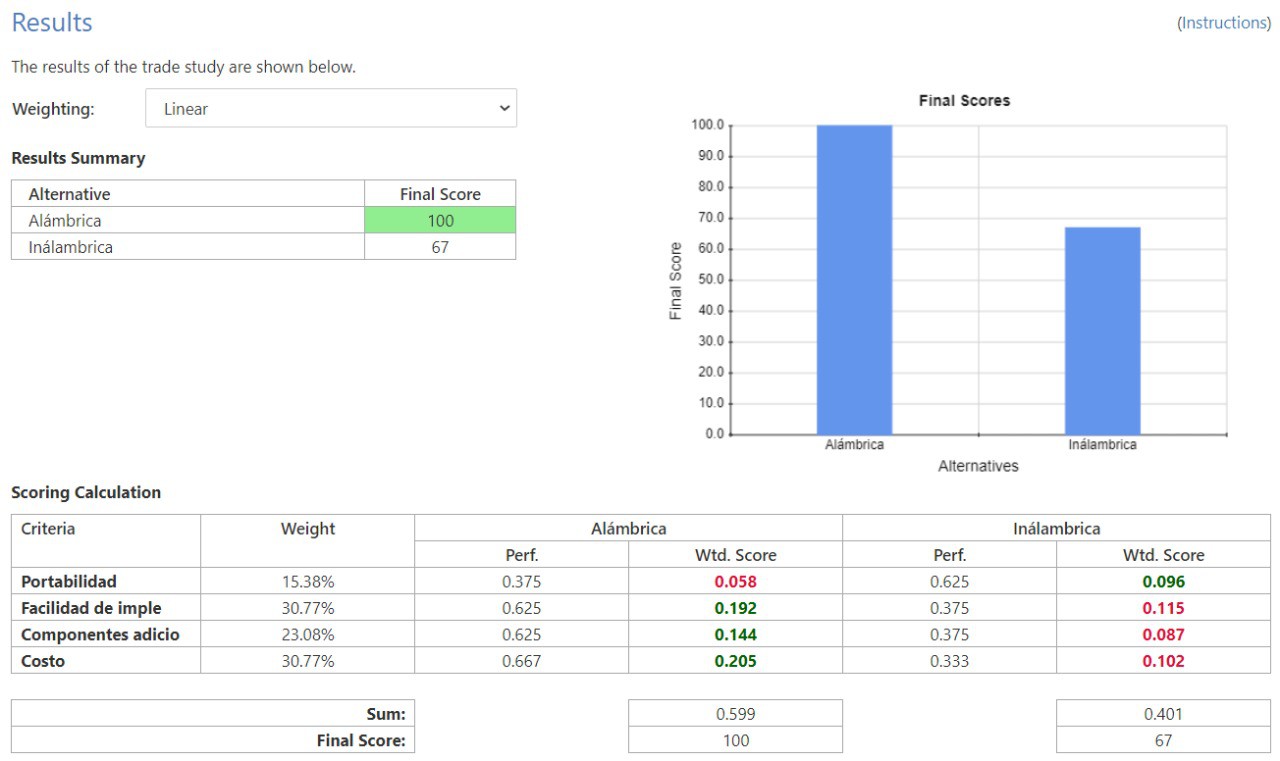
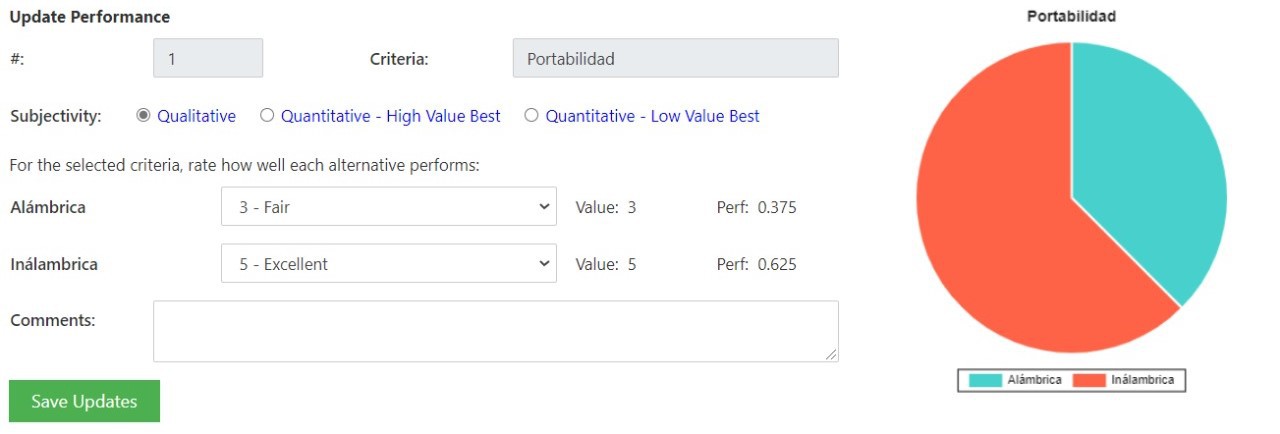
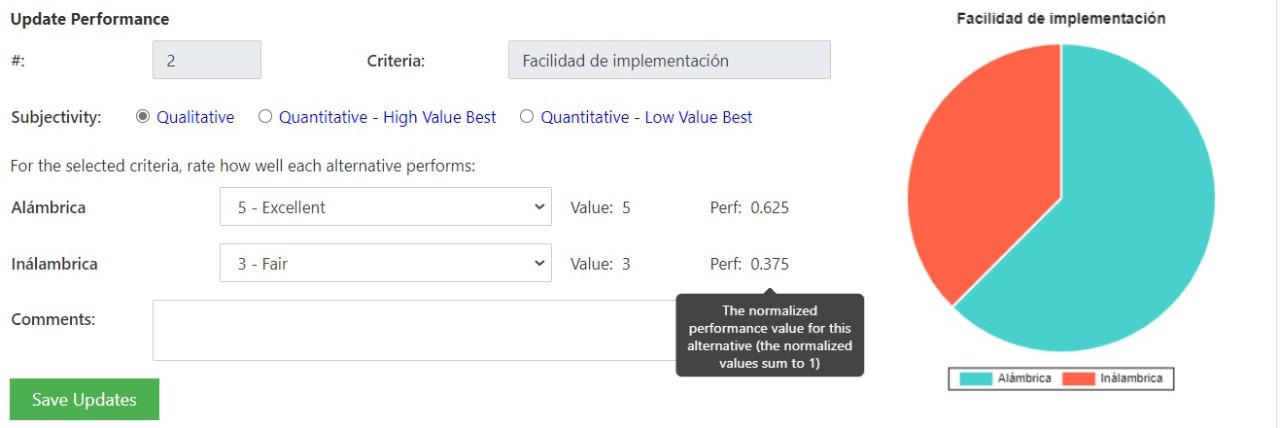
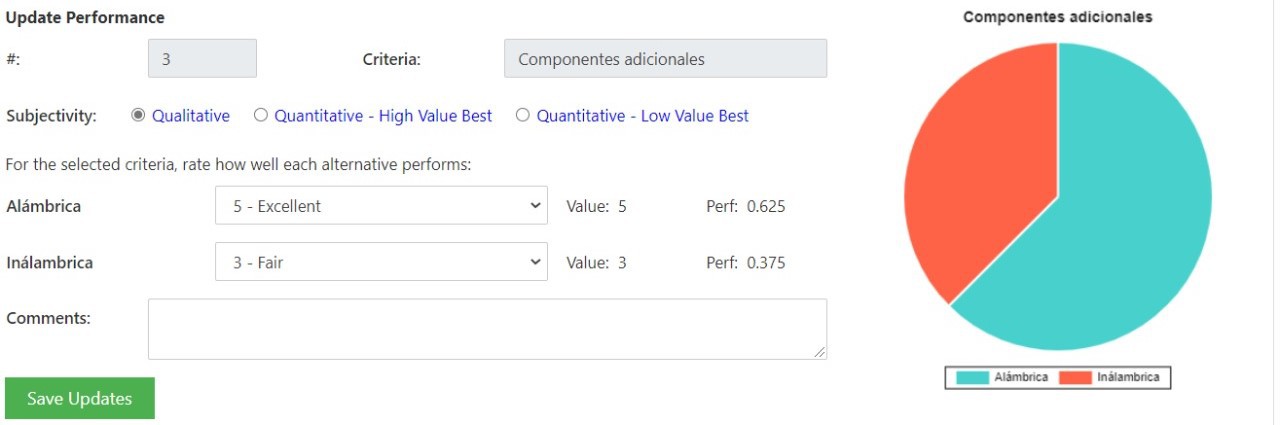
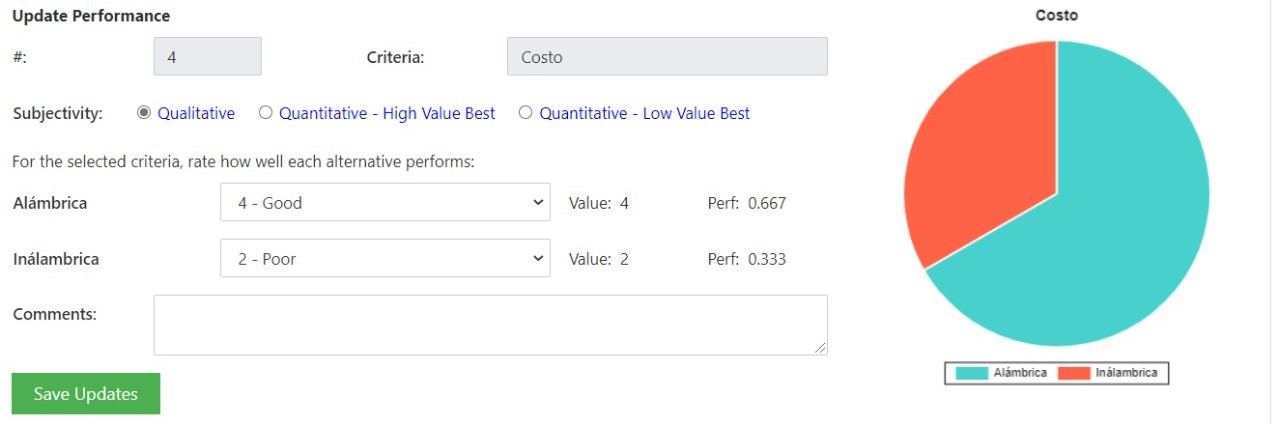
Se consideraron las opciones de comunicación alámbrica e inalámbrica debido a facilidad de implementación para el primero y que ya se contaba con el módulo Wi-Fi ESP8266 previo a empezar el proyecto para la comunicación inalámbrica. Los criterios que se le otorgaron un mayor peso fueron la facilidad de implementación y el costo, esto debido a que el equipo deseaba evitar complicaciones de comunicación y, al mismo tiempo, se tenía un presupuesto limitado para la realización del proyecto. El siguiente criterio con mayor peso era el de utilizar componentes adicionales para la comunicación, esto ya que el equipo deseaba que dicha comunicación fuera de lo más práctica posible. Por último, el criterio con menor peso es el de portabilidad. Con estos criterios y pesos asignados a cada uno, se llega a la conclusión que la mejor opción de comunicación es la de tipo alámbrica.

Criterios de selección:

Esquemáticos, BOM y power budget diseño electrónico 

Esto se encuentra adjunto en la sección de archivos. En la parte de esquemáticos se muestran las conexiones de los componentes que se utilizan de la placa Arduino UNO y los servomotores. El BOM se encuentra en un libro de Excel donde se detallan sus componentes y precios. Finalmente el power budget en otro libro de excel donde se muestra el consumo de corriente por componente. 

Selección de fuente validada con el power budget

Inicialmente el trade study había indicado que la alimentación más adecuada era la conexión de tomacorriente a entrada DC del Arduino. Sin embargo, basado en los cálculos de Power Budget, la alimentación se realizará por medio de un adaptador AC-DC 5V 3A para los ocho servomotores y el Arduino con el puerto USB de la computadora. Este último se debe a que será necesario el envío de comandos para las rutinas de movimiento del robot. 

Matrices de parámetros de Denavit-Hartenberg y transformaciones de base

Basado en el modelo de Inventor se determinaron los movimiento de acuerdo a la convención de Denavit-Hartenberg (DH) necesarios para determinar la cinemática directa de una de las patas del robot. A través de la herramienta de Inventor para colocar sistemas de coordenadas de usuario (CSU) se realizaron las mediciones para obtener los valores numéricos de estos parámetros. 

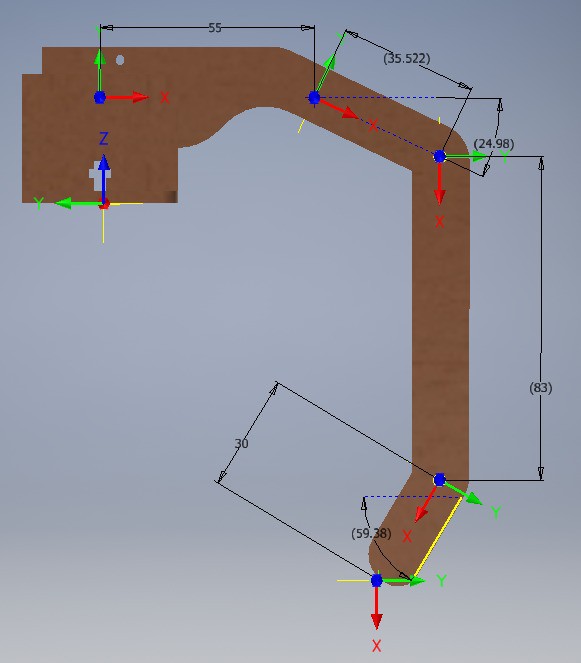
Como se había explicado anteriormente, cada pata del cuadrúpedo consta de 2 GDL, los cuales corresponden a los parámetros de la configuración q1 y q2. El resto de parámetros que se observan en la matriz de DH son dummy para representar la geometría de las patas en la simulación de Matlab. No obstante, los parámetros DH de las filas de q3 a q6 si son de utilidad para determinar la matriz de transformación homogénea de herramienta. Se utilizó la misma matriz de DH para las cuatro patas y luego se harán las distinciones entre ellas en la matriz de transformación de base. 

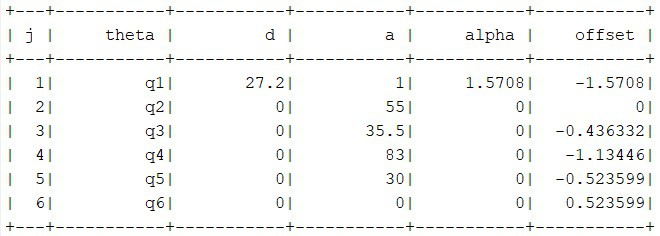
El marco de referencia inercial se coloco en el centro de la base del robot, el cual coincidió con el origen del assembly en Inventor. Utilizando la misma técnica de medición de parámetros se determinaron los valores de las matrices de transformación de base para cada una de las patas. 

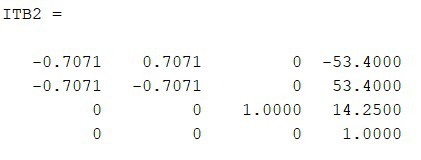
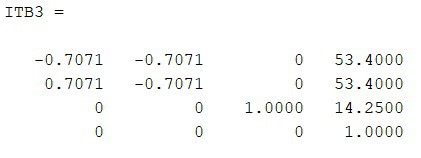
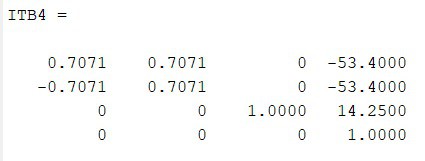
Rutinas de cinemática directa, diferencial y cinemática inversa

Para el cálculo de la cinemática directa, diferencial e inversa se desarrollaron códigos en Matlab, los cuales están adjuntos en la sección de archivos. 

Estos códigos cuentan con dos parámetros de entrada: la configuración y la selección de pata. Esto para desarrollar rutinas de forma más eficiente. En el código de cinemática directa se generan las matrices de transformación base y la de transformación de herramienta para luego hacer la multiplicación con la cinemática directa que se obtiene con la función getFK.m. Con respecto a la cinemática inversa se seleccionó el algoritmo de Levenberg-Marquardt por encima de la traspuesta y la pseudoinversa. La traspuesta presenta una convergencia continua pero es muy lenta, es decir que requiere demasiadas iteraciones para llegar al punto deseado. La psudoinversa presenta una sensibilidad alta a las singularidades. Por tal razón se determina que el algoritmo de Levenberg-Marquadt es la opción óptima ya que no presenta las imperfecciones de los dos métodos, es decir, presenta una buena robustez en contra de singularidades y, además, presenta una convergencia suficientemente rápida. 

Visualización de la cinemática del robot

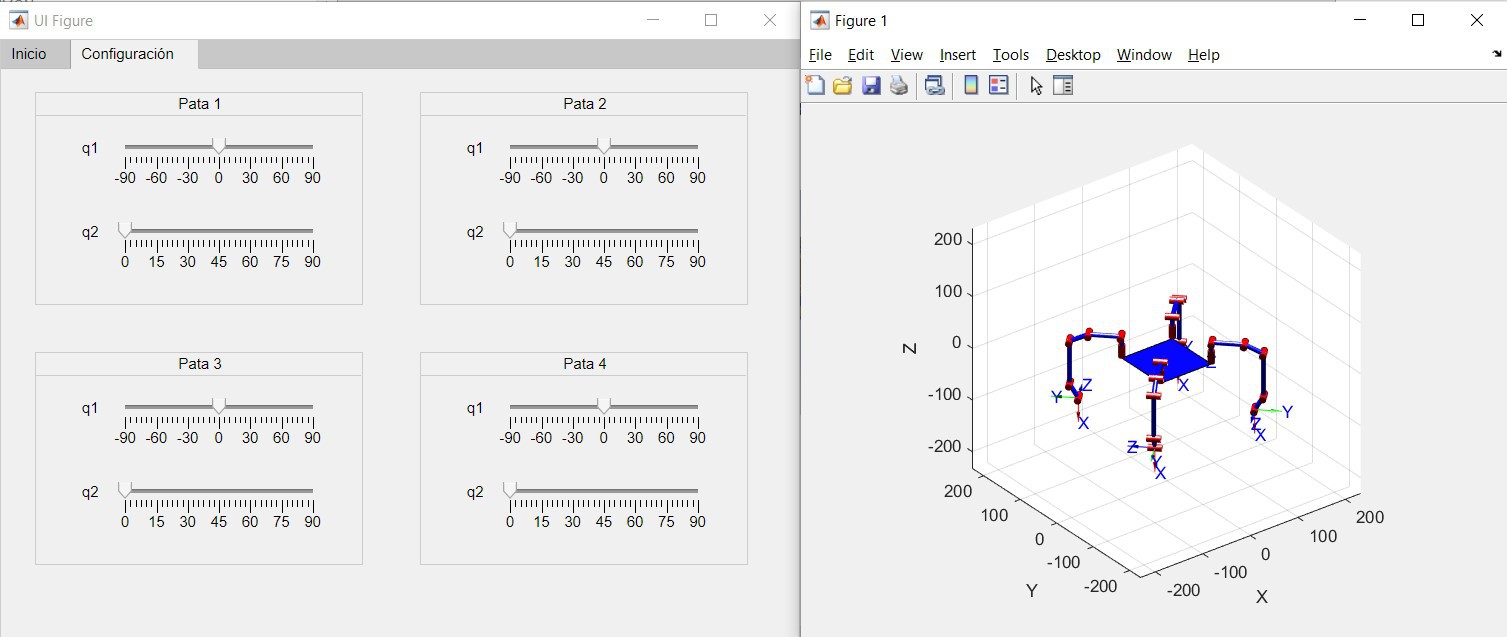
Se desarrollo una interfaz de gráfica de usuario (GUI) en Matlab con la cual, a través de sliders es posible modificar los parámetros de configuración q1 y q2 de cada pata. Los sliders que modifican al parámetro q1 están limitados en el rango de [-90°, 90°], mientras que los correspondientes para el parámetro q2 se encuentran en el rango de [0, 90°]. Cabe mencionar que la GUI se implemento utilizando la Robotics Toolbox de Peter Corke, específicamente el objeto creado por SerialLink y su función plot(). Esta función muestra una animación gráfica del robot basado en el modelo cinemático. 

Generación y ejecución de trayectorias

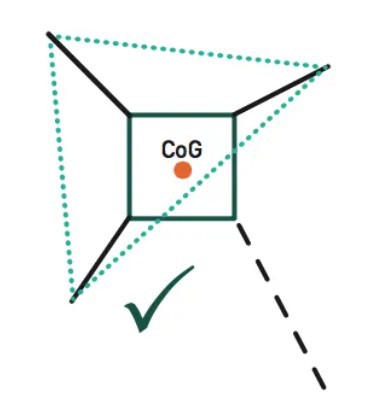
Las trayectorias de movimiento deben garantizar que el cuadrúpedo tenga estabilidad en todo momento. Existen dos tipos de estabilidad: pasiva y activa. En este caso se opto por la estabilidad pasiva ya que no necesita ninguna señal de control externa para mantener al sistema de forma erguida. Con el tipo de estabilidad definido se procede a establecer al creep gait como el patrón de movimiento a utilizar, el cual consiste en mantener tres extremidades en el suelo mientras se extienda la cuarta. Haciendo este proceso se garantiza que el centro de gravedad del sistema se encuentre siempre dentro del triángulo formado por las tres extremidades que tienen contacto con la superficie, tal y como se muestra en la siguiente figura. 

Como se había mencionado antes, cada pata del cuadrúpedo diseñado cuenta con dos grados de libertad, donde q1 corresponde al que permite rotación y q2 el que permite subir o bajar la extremidad. Cabe mencionar que, según la forma de montaje del sistema, q1 es 90° cuando la extremidad se encuentra en diagonal, mientras que q2 es 0° cuando la extremidad tiene contacto con la superficie. Partiendo de esto se procede a definir el patrón de movimiento hacia adelante, el cual consiste en la serie de pasos mostrados a continuación. 

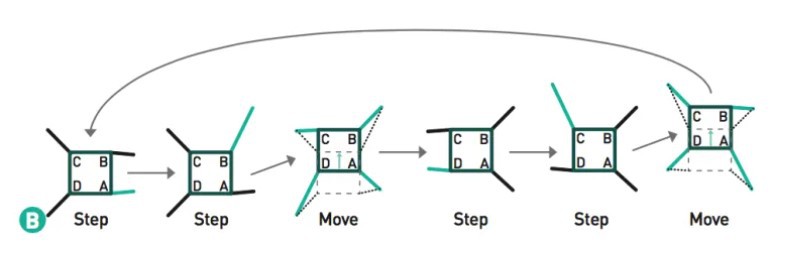
  1. El movimiento comienza con las dos extremidades del lado derecho extendidas hacia adentro y las otras dos, correspondientes al lado izquierdo, en su posición inicial colocadas en diagonal (90° en q1).
  2. La extremidad superior derecha se levanta un aproximado de 22°, rota 70° para luego bajar y estar nuevamente en contacto con la superficie. 
  3. En el siguiente movimiento todas las extremidades se mueven hacia atrás con el objetivo de empujar el sistema y así moverlo hacia adelante. Cabe mencionar que en este paso no existe un levantamiento de las piernas ya que es necesario utilizar la fricción para producir el movimiento. Siguiendo la denominación de la figura mostrada anteriormente, las extremidades C y A rotan 55° y D junto a B rotan 15°. 
  4. Se repite el mismo proceso pero ahora del lado izquierdo del cuadrúpedo. La extremidad izquierda inferior debe levantarse 22°, rotar 70° para luego bajar y estar en contacto con la superficie. Como se puede ver, esto es un reflejo de lo que se tiene en el paso uno.
  5. La extremidad izquierda superior se levanta 22°, rota 70 ° y baja para establecerse nuevamente en el suelo. Esto es un reflejo de lo que se tiene en el paso dos. 
  6. Nuevamente se deben mover las cuatro extremidades para generar el movimiento hacia adelante. En este caso las extremidades C y A rotan 15°, mientras que B y D rotan 55°. Finalmente la extremidad A se eleva 22°, rota 70° y vuelve a bajar para colocarse en la posición inicial para empezar nuevamente el ciclo. 

La generación de trayectoria se realizó en el espacio de configuración (C-Space), por lo cual fue innecesario valerse de la cinemática del sistema. Para determinar los ángulos de rotación y elevación descritos en la secuencia de pasos anteriores se utilizó la interfaz gráfica desarrollada anteriormente en Matlab. Basándose en la simulación del movimiento de las extremidades y realizando diversas pruebas con el robot físico, se logró determinar que los ángulos descritos anteriormente eran suficientemente buenos para obtener resultados adecuados para la aplicación. 

Sabiendo la cantidad de grados que debía rotar cada servomotor se procedió a generar una trayectoria (Excel) con más puntos para obtener un movimiento suave. Para el caso donde el cambio eran 22°, 55° y 15° se utilizaron 11 puntos intermedios, y donde el cambio era 70° se utilizaron 14 puntos. Tomando en cuenta esto último se obtuvo una matriz de 166x8 para la trayectoria completa. La cantidad de columnas representa las juntas/grados de libertad presentes en el sistema. 

Realizar los movimientos hacia la derecha, izquierda y atrás es equivalente a rotar el robot sobre su propio eje y moverse nuevamente hacia adelante. Sin embargo, en este caso no se desea hacer directamente dicha rotación, más bien el sistema debe presentar movimientos parecidos a los de un cangrejo. Por ello, los movimientos mencionados anteriormente únicamente representan un cambio en el posicionamiento de las extremidades, tal y como se muestra en la siguiente imagen. Es importante recalcar que las extremidades se denominaron de 1 a 4, donde cada una se encontraba en la posición tal y como se ejecuta en la simulación de la interfaz gráfica. 

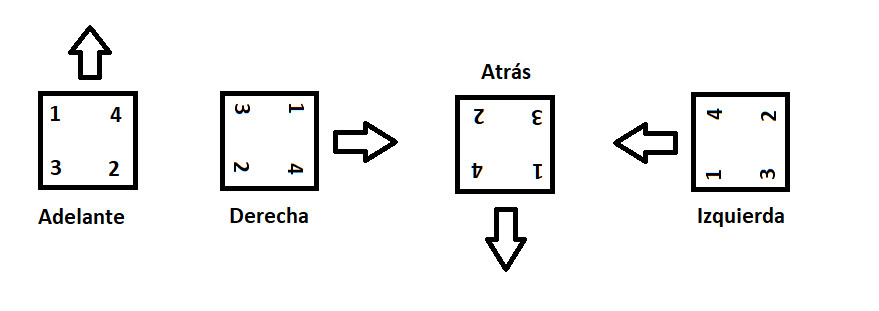
Por lo tanto se puede ver que para el caso del movimiento hacia la derecha la extremidad 2 toma los valores de 4, 4 de 1, 3 de 2 y 1 de 3. Este mismo principio se aplica para los otros dos tipos de movimiento. 

Como se había mencionado en secciones anteriores, se utilizó el microcontrolador Arduino UNO para la implementación de estas trayectorias. Por cuestión de espacio de memoria se colocó una única vez la matriz para la trayectoria hacia adelante, la cual fue definida de 8 bits ya que ningún dato superaba el valor de 255. Se procedió a realizar rutinas a través de ciclos for para cada tipo de movimiento, donde la diferencia en cada una era hacer el intercambio de extremidades tal y como se explicó anteriormente, pero siempre utilizando la misma matriz. Al mismo tiempo, se habilito el puerto serial para el envío de comandos para la ejecución de alguna rutina. El comando "1" implica realizar la rutina hacia adelante, "2" hacia la derecha, "3" hacia atrás y "4" hacia la izquierda (código disponible en la sección de archivos). 

Problemas