It does not seem to matter, in a mathematical perspective, where/when you introduce the datum perturbation. However it matters for efficient scheduling in any somewhat advanced processor, or even simply electronic circuits.
And for safety it can also do a great difference.
The trivial version of the iteration does not fully exploit the available parallelism. The following dependency graph shows an enhanced version on the left, with the trivial version on the right :
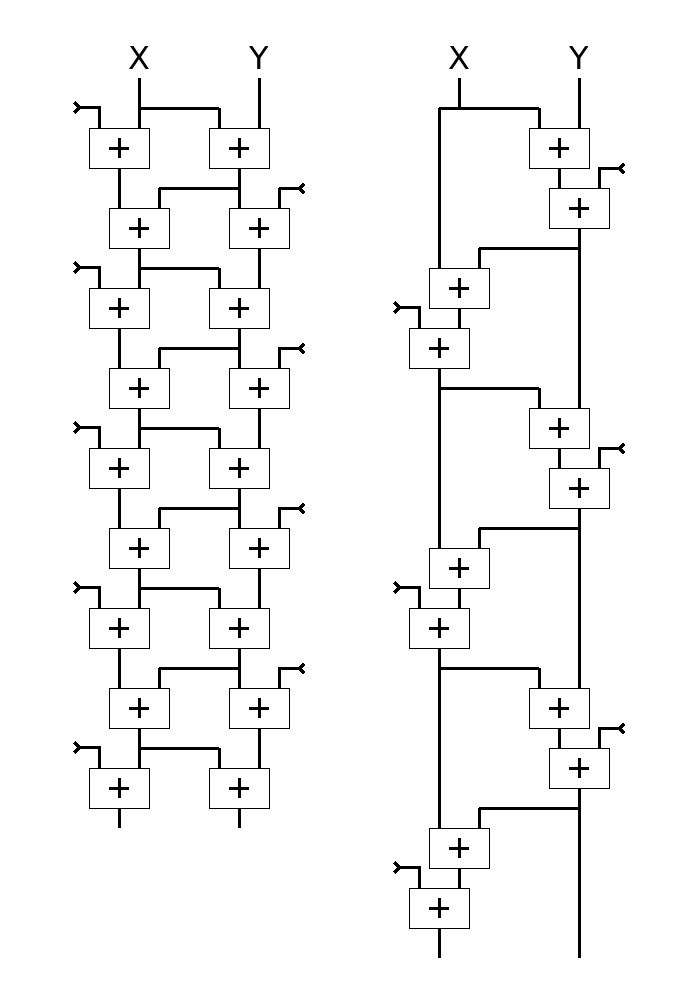
As we see in a later log, the version on the right is not only slower, but has a flaw that would allow external data to compromise the internal state and push the algorithm in a degenerate state.
The left version is a bit more tricky to write - yet not really that much, but it's also 2× faster on any superscalar or even OOO core.
All I had to do was move where the external data are introduced, if possible outside of the "critical datapath". This comes at the cost of one or two temporary data, here tx and ty for clarity.
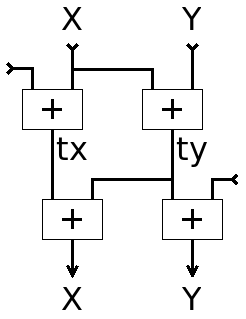
The corresponding C code is pretty easy to extract from the graph :
uint64_t X, Y, tx, ty; uint32_t buff*; tx = X + (uint64_t)(buff[i]); ty = X + Y; X = tx + ty; Y = ty + (uint64_t)(buff[i+1]);
If you have 2 integer pipelines (which is not exceptional these days), they will be fully busy.
If on top of that you have a Load/Store Unit that can process 1 load per cycle, you can compute 32 bits per cycle. You can also duplicate and interleave two adjacent computations for increased throughput (as some IP checksum algos do) and, since it is a linear operation, the blocks should be "reconcilied" every 40 or so cycles to prevent the effects of modulo truncations of the higher half of the registers. However, given the demonstrated occupancy of the pipelines, this should not be required... I'll have to explore and check the maths on this though.
Anyway, as promised, this algorithm shows a great efficiency with few efforts.
 Yann Guidon / YGDES
Yann Guidon / YGDES
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.