What is it ?

There is a question that bugs me for weeks now : what type of mathematical object is it ?

I have a quite decent knowledge of the usual types : integers, reals, complex numbers, and even some Galois fields over Z², for example. Quaternions, vectors and matrices are other types that are well defined. But the object under consideration puzzles me. Is it a ring, a field, a group, or something else ?

Let's start with the obligatory Wikipedia quote:

In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. In other words, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.

Formally, a ring is an abelian group whose operation is called addition, with a second binary operation called multiplication that is associative, is distributive over the addition operation, and has a multiplicative identity element.

So here is the new riddle : does addition even exist in this object ? The answer is easy for the previously cited types yet here, the elements are not numbers, but coordinates in a 2.5D closed space. Whether the carry counts as one individual dimension is still being debated. The description does not fit directly with a vector system. The behaviour is a bit reminiscent with a very weird Galois field but here, the "generator" generates only one half of a symmetrical set of coordinates (which I call orbits here). Really I know nothing of this kind.

So what can we say so far about this family of objects ?

It is a family of sets defined by a single parameter (called here w, or width)
Each set is organised as a vector space with coordinates X=[0..2^w-1], Y=[0..2^w-1] and C=[0..1], hence cardinality of 2^w+1 elements.
Each element has a predecessor and successor, defined by a reversible formula (with forward and backwards directions, already defined in other logs).
Elements (0,0,0) and (2^w-1,2^w-1,1) are their own precursor and successor.
Except for w=1, the space shows a symmetry and duality (invertibility?), where all elements (x,y,c) have an inverse value (2^w-(x+1), .2^w-(y+1), 1-c), with the same behaviour.
Since each point has a successor and a precursor, and the number of points is finite, the series of successors must be finite too, leading the series back to its first element, and this creates an "orbit".
Some values of w create a system with only two orbits (as calculated in this log) and these are the ones I'm seeking:
```
2, 3, 4, 10, 16
```
Other numbers may exist above 25 but have not been discovered so far.

Another interesting detail is the way the successor is calculated: Y gets the value of X. So in a way, when we map the coordinates on a 2D plane, each step represents a sort of rotation on this plane. This system makes me think of the logistic map r×x×(1-x), such as:

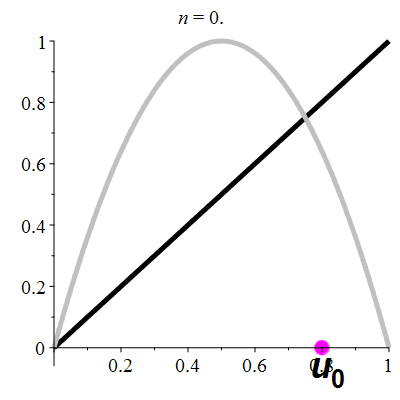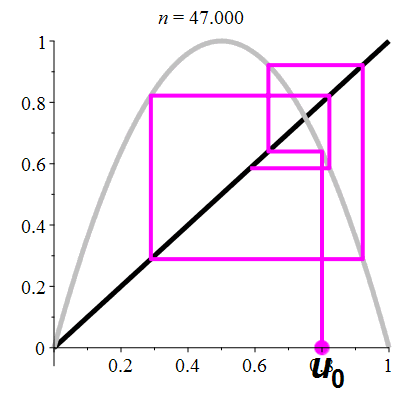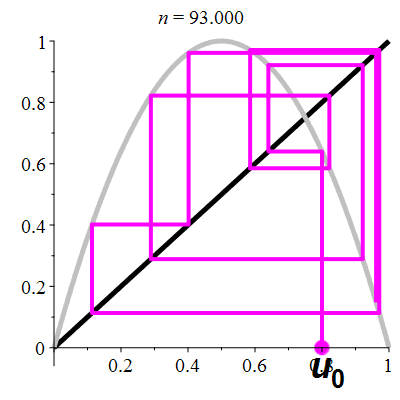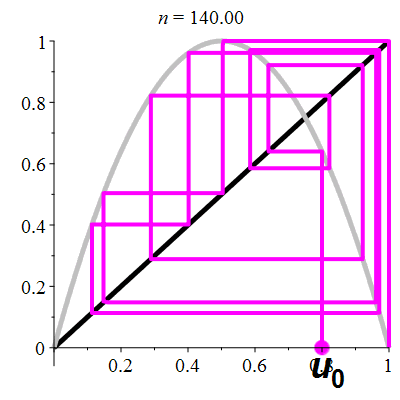
Of course it is not directly related, if only because here the values are integer, modulo 2^w and every overflow causes an increment of x. The other detail is that there is no parabola, no multiply/squaring and the guiding function is Fibonacci's series. Is there a link I'm missing yet?

Further theorising

A bigger enhancement

Discussions

Become a Hackaday.io Member