Latches and D-Flipflops have cause the biggest headache in every logic familiy I have implemented so far. This is no different with NE555 based logic. A straightfoward way would, of course, be to form a polarity hold latch out of 3 NAND2 gates. This would require 3 NE555, however, and seems to be a bit of a waste.

The NE555 has an integrated RS flipflop, meaning that a single NE555 should be sufficient for a latch. What is a bit tricky is to gate the data with the enable signal, so that the RS flip flop is either set for input=1 and EN=1 or cleared for input=0 and EN=0.

In the end I found a hacky way, using an NPN transistor as a pass gate. Since the NE555 logic is slows anyways, it does not matter that the pass gate is quite slow as well. The circuit is shown below.

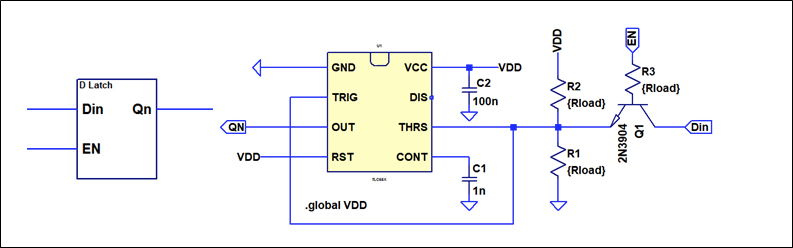
When the enable signal is low, the pass gate transistor Q1 is in a high ohmic state. The voltage divider formed by R1 and R2 will pull the input of the schmitt-trigger formed by the NE555 to VCC/2. This means that it will retain it's previous state, since neither of the switching threshold is reached. When EN goes high, the transistor becomes conductive and will pull the input high or low, depending on the state of "Din". If Din=0, the transistor is operated in reverse direction where it's hfe is rather low. Since the base current is equal to the current through R2, only a very low hfe is needed (1-2) to pull the input low.

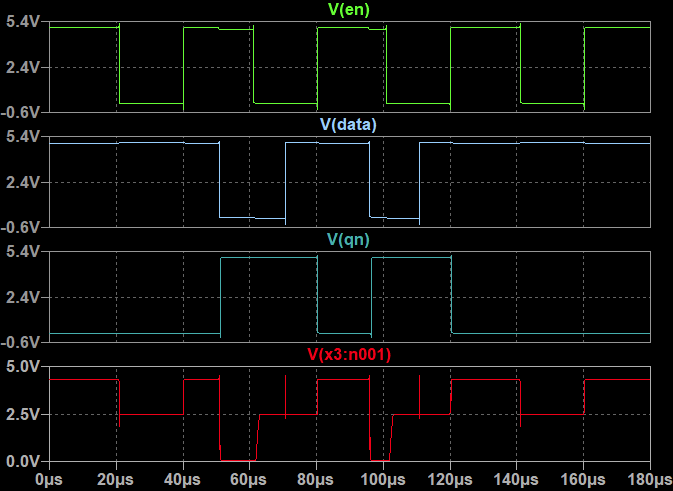
The simulation below shows how the latch works. The lowermost trace is directly from the TRIG/THRS input of the NE555. You can see that it operates on three voltage levels, either to set, clear or keep the state of the schmitt trigger / RS flip flop.

We can use two Latches and one inverter to form a full D-Flipflop.

If you feel that using a transistor is cheating: there is still the option of going to a latch with three NE555 as outlined above.

This concludes our basic gates and we can now build both combinatoric logic and registers.