When calculations are done 1 bit at a time, one should probably not expect blazing speed.
To measure the clock cycles per operations, I simply baked a 8-digit BCD counter into the system and increment it at each cycle, and reset to 0 at each new instruction. This is in top-level file of the design:
-- count clock cycles per instruction
cclkcnt: bcdcounter Port map (
reset => (RESET or i_new),
clk => hc_clk,
enable => (hc_status(1) and hc_txdready), -- only count when status is "busy" and not waiting for UART
value => c_cnt
);
i_new <= hc_status(1) when (hc_status_old = status_ready) else '0';
on_hc_clk: process(hc_clk)
begin
if (rising_edge(hc_clk)) then
hc_status_old <= hc_status;
end if;
end process;
i_new is the pulse (on hc_clk clock cycle wide) that gets generated when a new instruction execution starts. This is detected because CPU status goes from STATUS_READY to any of the STATUS_BUSY (bit(1) of status field is 1). The status is generated at each and every microinstruction (and unless stated otherwise, will be "busy"):
// Component interface signals
STATUS .valfield 2 values
ready, // waiting for input character
done, // input processed, will go ready on next clock cycle
busy, // processing
busy_using_mt default busy; // processing and needing the MT_8816
hx_txdready is the signal that comes back from UART sender. Because at 38400Hz (typically) this is slower than CPU speed, this wait time is excluded from the count (during this time counting is disabled).
Finally, the value of the counter is fed into the "hardware window" to display to VGA:
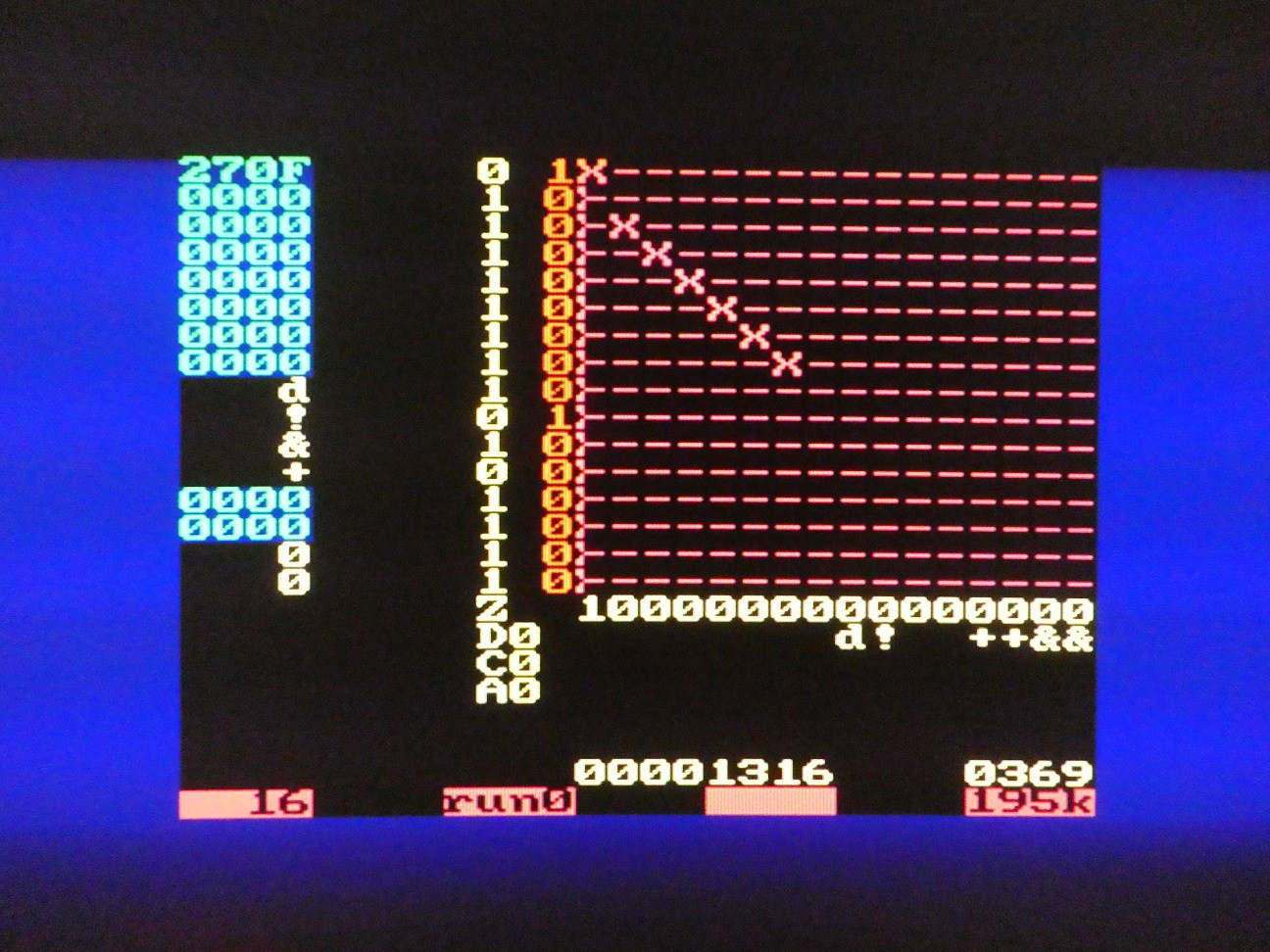
(measurement converting 9999 to binary in 16-bit mode, with tracing input and tracing output disabled, clock 195kHz)
| Operation | 16-bit | 32-bit | Notes |
| 0..F (enter digit into TOS) | 36 | 52 | |
| ENTER (push registers down, clear TOS) | 47 | 79 | |
| Z (clear TOS) | 46 | 78 | |
| N (clear all regs) | 39 | 71 | |
| R (rotate registers) | 47 | 79 | |
| U (duplicate TOS) | 48 | 80 | |
| S (swap TOS and NOS) | 48 | 80 | |
| < (shift TOS up) | 50 | 82 | |
| > (shift TOS down) | 50 | 82 | |
| + (add TOS + NOS) | 48 | 80 | |
| - (sub TOS - NOS) | 49 | 81 | |
| * (multiply TOS * NOS) | 51 786 | 83 2578 | Best: TOS = 0 Typical: all other |
| / (TOS / NOS) | 95 1384 | 127 4830 | Best: TOS = 0 (divide by 0 detected) Typical: all other |
| # (convert to BCD) | 1529 | 5493 | for arg 9999/99999999 |
| $ (convert to binary) | 1316 | 4656 | for result from above |
| Q (integer square root of TOS) | 16305 | 94195 | Worst: max argument |
General observations:
- As expected, when n bits need to be traversed once, the time is n + overhead, therefore O(n)
- For other operations, time is O(n^2)
- Algorithms have much overhead because in the middle of calculations switches must be turned on and off
- Some operations take same time regardless of the number of registers! For example R, N - while for parallel CPUs these would be O(r)
How to improve performance:
- In order to save microcode space, the pattern used is to turn off all switches ("nuke" alias in microcode) then set the matrix (e.g. nop() for diagonals etc.) and then turn on/off the differences. Instead, the exact switch states from step before could be analyzed and only differences applied
- Division could be optimized by simultaneously generating both outcomes of the divide step and pick one instead of substract/restore used here. Again, the optimization was for less code so more operations can fit into 256 words of microcode. Division is used in Heron's iterative method to calculate isqrt() so that would benefit a lot too.
- Speed up setting up the switches: for example two switch matrixes could be used, one to use for calculations, while during that time in the background another is set up for next step. This way most of the switch overhead could be eliminated, and just driving bits serially would remain.
 zpekic
zpekic
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.