Like in most calculators, digits are entered the TOS (top of stack) register from right, pushing all other digits up for 4 bits, with MSN (most significant nibble) lost.
There are many ways to accomplish this, but the approach here is a bit complicated because the optimization was done to minimize microcode needed:
- When entering digits, the input register ("instruction register") contains the ASCII code of the digit
- First, R12 and R13 are loaded (these are parallel loadable) - R12 with bit reverse of lower 4 bits of ASCII code (e.g. A = 0x41 = 01000001 so with 1000) and R13 with a correction value which is 1101 (.data value alias)
- R12 and R13 are connected to inputs of the adder, and TOS as output, carry is cleared, nop1() matrix is set up for rest of registers
- 4 shifts down are made for all registers except TOS which is shifted up - this way the 4 bits of correct value appear in LSN of TOS (opr = m2_d2_d2)
- bitcnt is now loaded with n - 4
- all registers (except TOS which is not shifted) are shifted down until bitcnt is 0. This means that they are shifted n times, so they remain with same value (opr = np_d2_d2)
...
.map 'a';
.map 'A';
.map 'e';
.map 'E';
data 0b1101, goto hexchar; // correction from reverse ASCII is 11
...
hexchar: load_bitcnt 3, c_flag <= zero, nuke, matrix_nop1();
connect row_const to col_adc1;
connect row_direct to col_adc2;
connect row_sum to col_tos;
STATUS = busy_using_mt, opr = m2_d2_d2, bitcnt <= dec, if bitcnt_is_zero then next else repeat;
disconnect row_sum from col_tos, bitcnt <= max;
connect row_tos to col_tos, bitcnt <= dec;
bitcnt <= dec;
bitcnt <= dec;
bitcnt <= dec;
STATUS = busy_using_mt, opr = np_d2_d2, bitcnt <= dec, if bitcnt_is_zero then nextchar else repeat;
State before shifts:
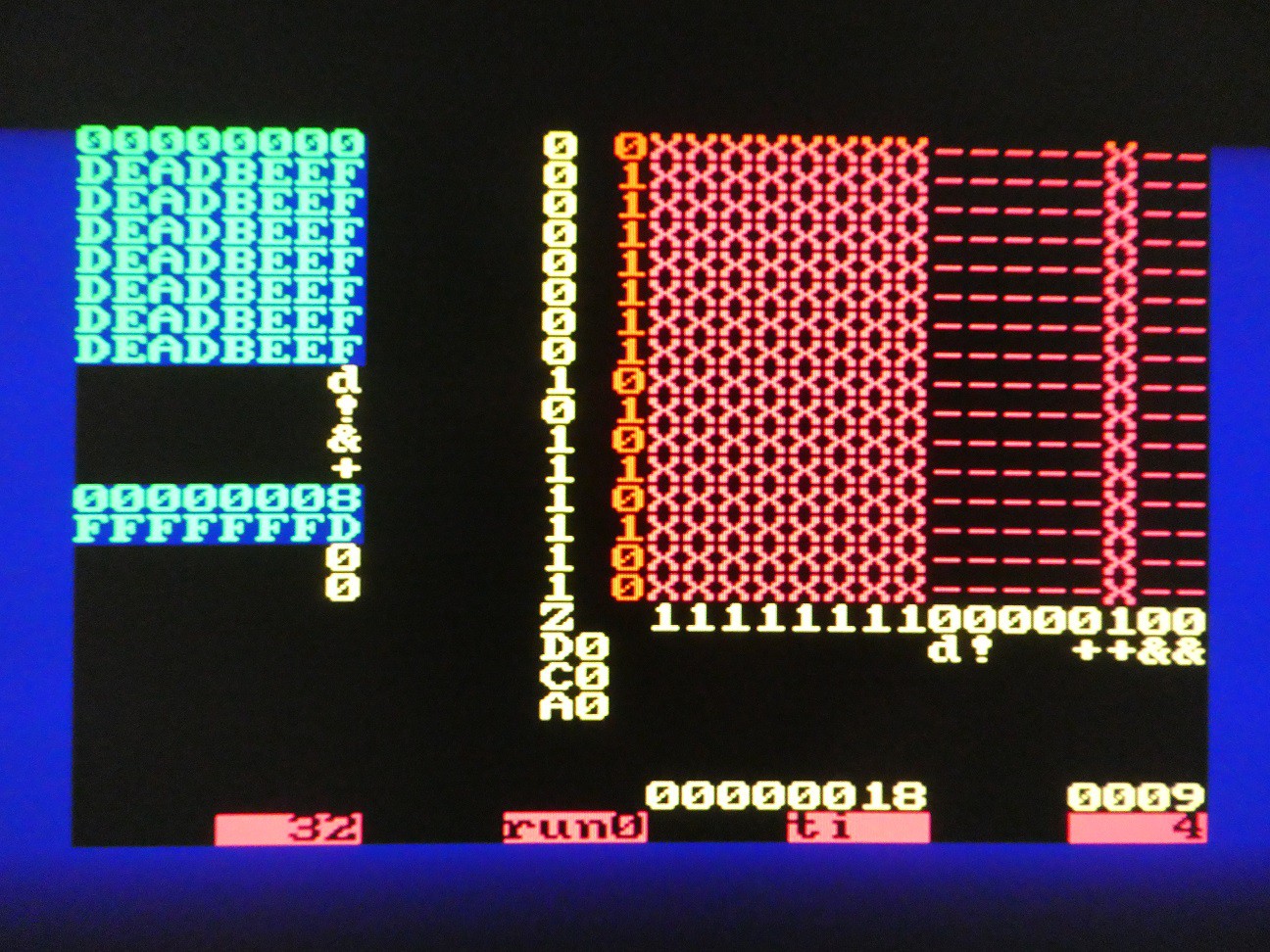
State after the shifts (digit A was entered, switch is position 0, 0 could be stayed off):
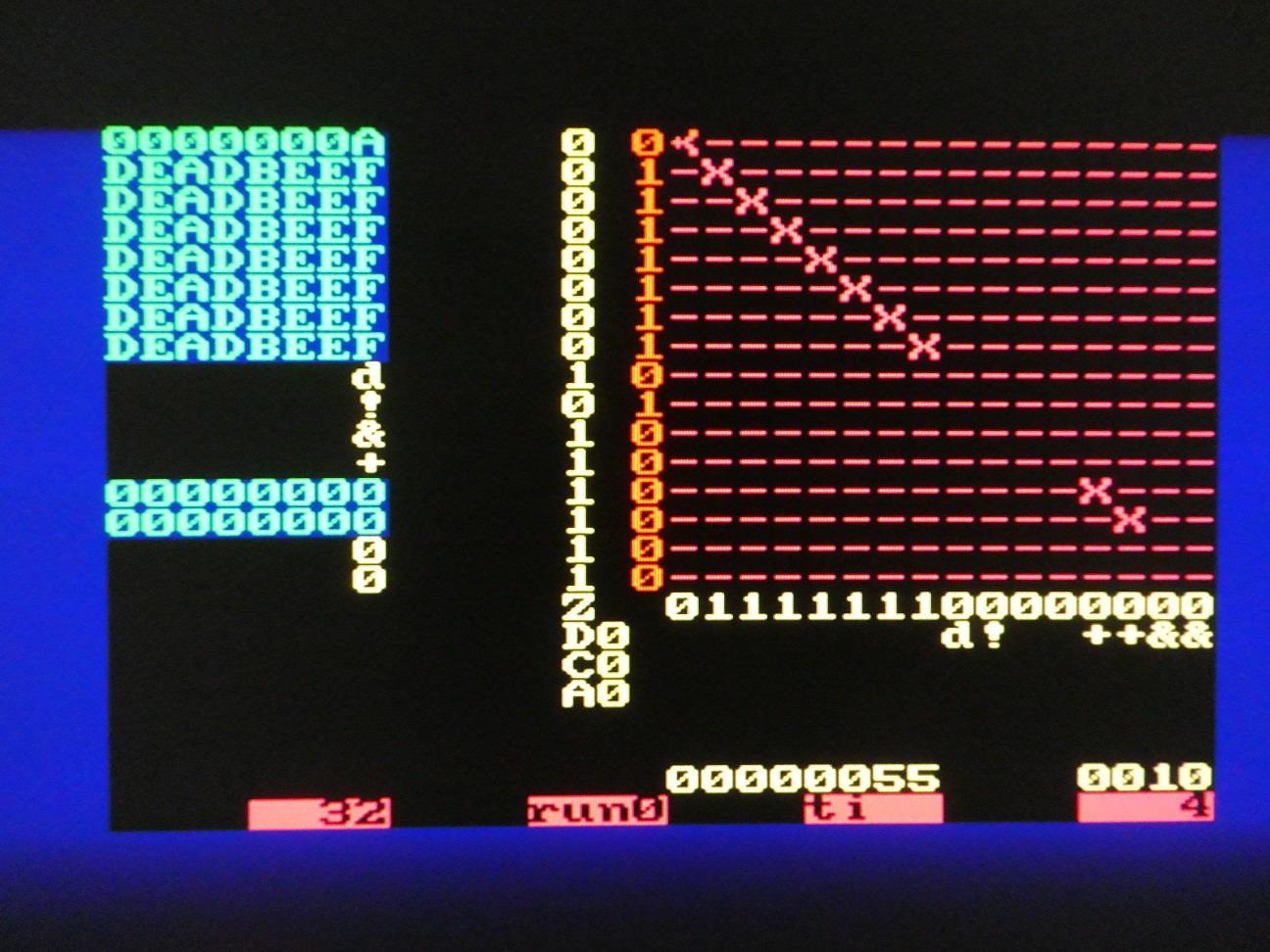
 zpekic
zpekic
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.