Game of Life bit-parallel algorithm

The article is out !

I have about 14 pages in GNU/Linux Magazine France #213 where I go through all the optimisation process and go even further.

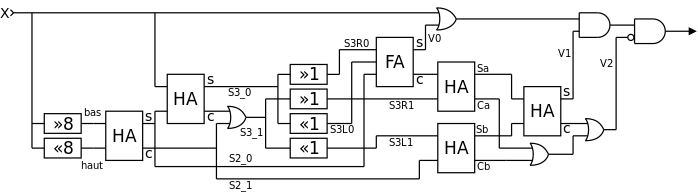
This article goes beyond the methods shown so far and I will try to develop them. The AVX SIMD extension brings some significant advantages and require a deep redesign of the algorithm but the basic ideas remain the same, summarised in the following graph:

I'll have to update the project, or maybe create a new one. Meanwhile, I'm pretty proud :

I just uploaded another version of the C file, this time with a copy-paste-adjust-warnings block from the JS version, and it worked right away.

For the record, you have to press ENTER to compute the next iteration. Add to this the cost of displaying data through the Xterm and you understand that it's far from the true speed that this algo can reach. But I'll optimise speed for #AMBAP: A Modest Bitslice Architecture Proposal later.

For now, I rejoice that it worked just like I expected :-)

                       #
                     ####
            ##     #### ##         ##
          #  #   #   ## ###        ##
 ##      #       #   ## ##
 ##      #      #   #####
         #       ###   #
          #  #
            ##

                         #
                          ##
                         ##

              ####
             # ## #
             ##  ##
             ##  ##
             # ## #             # #
              ####               ##
                                 #

I've just uploaded a C file that works with 64 bits (though it can be anything) and provides a skeleton for the data shuffling that reduces memory usage.

There is no double-buffering, the cells are computated "in place". To prevent time-distorsions (the result being directly used for the next iteration), the current result is written to the WriteBuffer variable. This variable is then written back to memory after the past value is read (again).

    L1=world[i-1];          // make sure we read
    world[i-1]=WriteBuffer; // the value of t-1, not the
                            // result computed in the last iteration
    L2=world[i  ];   // I know, a rotating register barrel
    L3=world[i+1];   // would work better but not for AMBAP

WriteBuffer = L1+L2+L3;

This helps me check that the ranges of indices can be dynamically adjusted. For example, with the following initial configuration:

start: 13

                         #
                       # ##
             ##      ## ## #       ##
            # ###    # #  ##       #  #
 ##        #  # # #   # #  #       ####
 #  #      #   # ### # ####        ####
 ####       ## #### # # #  #       #  #
 ####      ## ### #### #  ##       ##
 #  #       ## #### ### ## #
 ##        #   # ###   # ##
           #  # # #      #
            # ###
             ##
               ##
              # # #
             #  # ##
            #    # ##
            #  # # # #
            #### ## ##
            #### ## ##
            #  # # # #
            #    # ##
             #  # ##
              # # #
               ##
max=40

After a few cycles, the range has grown :

start: 10

                         #
                       #  ##
             ##      ### # # #     ##
            #### #    ####   ##     #  #
 ##        #####  ## ###  ## # #     ####
  #  #       ##### # ##### # ###   ###    #
   ####    # ####   ##   # #    #  #    ###
 ###    #   #   # ## #    ##    #       #  #
 #    ###   #  # # # ##    #    #       #  #
      #  #  # # ### # # # ##    #  #    ###
      #  # # ### ###      ##    #  ###    #
 #    ###   # # ### # ### ## ###     ####
 ###    #   #  # # # ##  ### # #    #  #
   ####     #  # ### # #  #  ##    ##
  #  #     # # ### ## # ## # #
 ##           ###   # ##  ##
           # ##    ####  #
            ##     #####
              # ##  # ###
            #  ##   #### #
            ###### #      #
             # # ##### #  #
             # # ##### #  #
            ###### #      #
            #  ##   #### #
             ### #  # ###
              # # # ####
            ### ## # ##
             #### #  #
              ###  #
               ##
max=43

The adjustment of the last line is done with the variable run: it is first cleared to 0 then set to the line number where the line is not empty. This value is then assigned at the end of the scan:

  MaxLine=run;

MaxLine will be the upper limit for the next time step, but it should preserve the previously mentioned "margin" for the growth of new cells beyond the last line. That's why run is set with a little offset, inside the loop:

    if (WriteBuffer)
      run=i+2;  // push the end of the work range

Dealing with the start index is a bit more tricky but run provides us with a way to handle it nicely. It remains stuck to 0 while empty lines are found so we can increase MinLine as long as run is cleared. The complete code is simply:

    if (WriteBuffer)
      run=i+2;  // push the end of the work range
    else
      if (run==0) // no life found yet
        MinLine=i-1; // push the start of the work range

I uploaded GoL.js and GoL.html. They don't "work" yet but they allowed me to test the following, functional code:

    L2=world[i];
    L1=world[i-1];
    L3=world[i+1];

    // half adder:
    S20 = L1 ^ L3;
    S21 = L1 & L3;
    // full adder:
    S31 = L1 | L3;
    S30 = S20 ^ L2;
    S31 = S31 & L2;
    S31 = S31 | S21;

    // Sum LSB
    S0 = (S30>>>1) ^ S20;
    S0 = (S30<< 1) ^ S0;

    // LSB Carry
    S0C = (S30<< 1) | S20;
    S20_= (S30<< 1) & S20;
    S0C = (S30>>>1) & S0C;
    S0C = S0C | S20_;

    // Sum middle bit
    S1 = S31>>>1 ^ S0C;
    S1 = S31<<1  ^ S1;
    S1 = S21     ^ S1;

// Inhibit
    INH = S31<<1 & S21;
    S1_ = S31<<1 ^ S21;
    C2 = S31>>1 & S0C;
    INH = INH | C2;
    S2_ = S31>>1 ^ S0C;
    S2_ = S2_ & S1_;
    INH = INH | S2_;

    X2 = S0 | L2;
    X2 = X2 & S1;
    X2 = X2 & ~INH; // The result is now in X2