YAMS Yet Another Merge Sort

One BIG conceptual challenge with sorting algorithms is to put each new datum as close to the right place as possible on the first try, so the actual running time gets closer to O(n). The n×log(n) part comes from recursively handling more and larger buffers so the smaller and the fewer, the better and faster.

If one datum is placed at the other side of the range, then it will usually perform log(n) operations to reach the final position, by leaps and bounds of more refined lengths.

That's why hash-tables and radix/bucket sorts are so efficient (on top of having no comparison with the neighbours) : Data are placed as close as possible to their definitive location, so there are fewer comparisons and moves to perform.

But in a hybrid sort algo, this is less obvious.

....

I was looking at the "shared stack" system and beyond its allure, I found that there is a deeper structure and organisation that needed to be addressed, as it seems even more promising.

Do you remember 2s complement signed numbers, and how they map to unsigned integers ? Also, look at ring buffers and how they can wrap around integer indices, using modulo addressing. Look also at how we can take one problem from both ends, as we did just before with the basic merge sort turned into a 2-way merge sort.

Shake it well and serve with an ice cube.

So this gives a "working area" that wraps around, with modulo addressing. Start by putting the first data run in the middle of the working area but since this is modulo, there is no middle anyway. So we start with a point, an origin, and we can work with data on both ends of the dataset mapped to the working area.

And this brilliantly solves a BIG problem of fragmentation I had with the merge sort, which is not usually "in place". If I want to merge sort 2 runs that sit on the "free end" of the data set. Usually, the "other end" sits at address 0 and is stuck there. One needs to allocate room "after"/"beyond" the "free end" of the data set, perform the merge there and move the merged-sorted block back to the origin.

Forget that now !

Since the "modulo addressing" doesn't care where the start is, there are two ends, and we'll use the FIFO/ring buffer terminology : tail and head. These numbers/pointers respectively point to the lower and higher limits of the dataset in the working area. Memory allocation becomes trivial and there is no need to move an allocated block back in place : just allocate it at the "other end" !

Let's say we have 2 runs at the head of the data set: we "allocate" enough room at the tail and merge from the head to the tail. And head and tail could be swapped. The dataset always remains contiguous and there is no fragmentation to care about ! When the whole dataset must be flushed to disk for example, it requires 2 successive operations to rebuild the proper data ordering, but this is not a critical issue.

Which end to merge first ? This will depend on the properties of the 2 runs at both ends. Simply merge the smallest ones, or the pair of runs that have the smallest aggregated size.

This changes something though : the "stack" must be moved away from the main working area, and since it will be addressed from both ends (base and top), it too must be a circular buffer.

What is the worst case memory overhead ? It's when the sort is almost complete/full,  and a tiny run is added and merged, thus requiring 2x the size of the largest run due to the temporary area. In a pathological case, if memory is really short, a smarter insertion sort would work, but it would still be slow...

This can work because the main data set is a collection of monotonic runs. They are longer "in the middle" but are not in a particular order. Thus there are in fact 4 combinations possible :

• 2 heads to the tail
• 2 tails to the head
• 1 head added to the tail
• 1 tail added to the head

This is much more flexible, thus efficient than the "single-ended" traditional algorithms, because we can look at 4 runs at a time, with simpler heuristics than Timsort, thus fewer chances to mess the rules.

___________________________________________________________

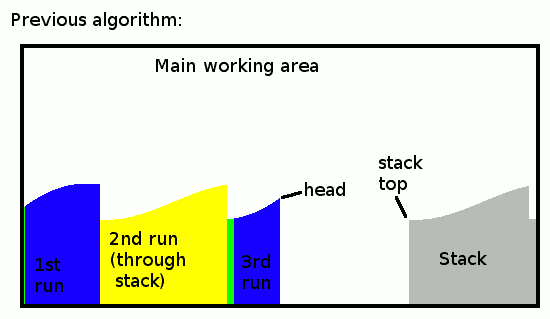
Here is how the previous iteration of the algo worked/looked:

New runs are added to the head when an ascending run was detected, or to the stack when a descending run is found. When the run ends, if it's a descending one, the stack is copied/moved to the head to reverse its direction. This last operation becomes pointless if we organise the runs differently.

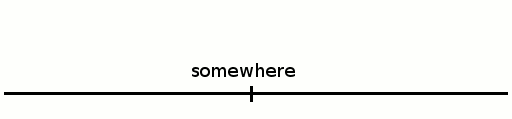
Let's simply remove the stack. Instead we add the runs in the middle of "nowhere" so there is no base, instead a void the left and to the right of the collection of concatenated runs.

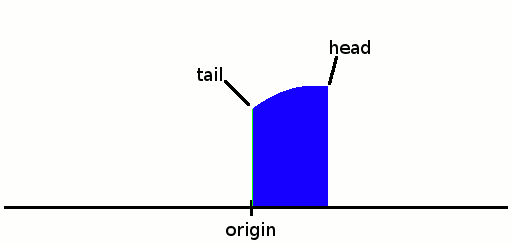
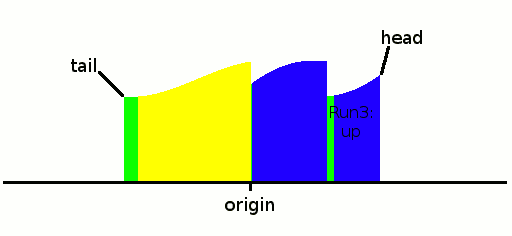
We put the first run there. The first/lowest occupied index is the tail, the higher/last is the head.

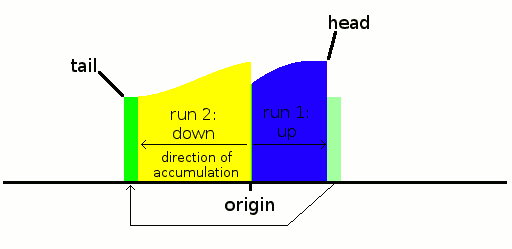
The "horizontal" parts (in green) are first written after the head. But if the slope is found to be downwards, this part is moved to the tail after the remaining data are reverse-accumulated from there (because we can't know in advance the length of the run). Usually, there are rarely more than a few identical data so the move is negligible. It could be avoided but the game is to get the longest run possible so this is fair game, as this block would be moved later anyway.

We could start to merge here but we can select a more favourable set of candidates if we have more data, like at least 4 runs, so let's continue accumulating. The next run goes up so it's accumulated on the head side.

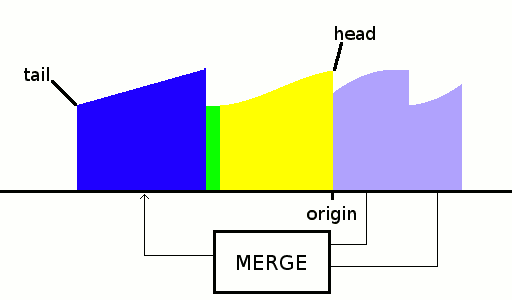
OK the stream ends here and we only have 3 runs, but we can already select the first pair to be merged: run1 and run3 are the smallest so let's merge them. Since they are on the head side, let's "allocate" room on the tail side:

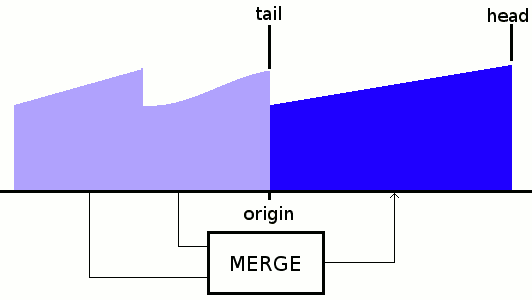
And now we can merge the final run to build the result, and since there are only 2 runs to merge, the result can go either on the tail or the head:

Here we see that the merge sort has an inherent space constraint, so the final merge requires at least 2× the total space overall.

This example used a 2-way merge operation, but ideally more ways (4?) would be better.

The great aspect of using wrap-around addressing is that it can handle any combination and worst-case situation, like when there are only up-runs, down-runs and even alternating runs. The origin does not matter so the whole contiguous block could move around at will with no consequence.

...........

.

.

Edit:

OK there might be a small limitation to the scheme I presented above. Ideally we would want to merge more than 2 runs at a time to save time, using 2 ends of each run to parallelise the process, but this is possible only when all runs are on one side, putting the result to the other side. Otherwise, that is : if 2 blocks are at opposite sides, then one of the blocks will already take the place of the merged result, for an in-place merge. This means that the merge sort can't use 2 sides of the runs, or it would overwrite the overlapping original run.

It's a bit less efficient but not critical.

This means I have to program several variations of the merge algorithms : one for sorting from the lower end first, another to sort from the higher end first, another to sort from both ends at the same time, and an extension to 3 or 4 runs at once. Selecting which one to use will require some heuristics, for sure... For example : if I merge 2 runs on opposite ends, which end should I favour ?

If you're French and of my age (or older) you might remember this weird ad:

"Eat the banana from both ends" it says. How inspiring.

The previous log Has anybody... introduced an idea that remineded me the ad, and then I had doubts.

But now I am confindent and the doubt is gone because I formalised the problem, and it was simple. The key is that the data must have only one way to be sorted, which is the case usually, right ?

If there is only one way to sort the data, then there is one way to sort it from the "higher values" as well as from the "lower values". In this case, both sorts can proceed by giving each parallel sub-task exactly one half of the data to process.

Again it's one of those things that sound so obvious when you find them, yet you can't find any reference in the open litterature. According to Knuth (through Wikipedia), merge sort was invented in 1945 by John von Neumann so at least someone should have thought about merging both ends at the same time in 77 years...

The new file sort_20220821.html.txt is out, with some interesting progress, such as a stack sharing the space of the main working area. More stress cases are available with the new buttons.

The algorithm so far is quite simple, built upon the previous iteration that detects increasing or decreasing sequences. While the input is monotonous, the values are stacked. If the value becomes increasing, the stack is flushed to the top of the working area and the next data are accumulated there until the end of the run.

Otherwise the data get pushed on the stack while they are monotonous or decreasing. When the run ends, the current run is popped in reverse order and moved to the working area, to make an increasing run.

After each run, the position and length of the run should be pushed on the stack but that will be for the next version... and once we have this list of elements on the stack we can merge-sort them as they should.

Now that #PEAC  on the schedule, I realise that no matter how I turn thing around, it always ends up with some sort of "classic" sorting so why even fight ?

Should I hash the hell out of the data set, I will get tons of buckets, sure, but each bucket must still be sorted anyway because that's how they are expected to be in the end, right... So what's holding me back ? I guess it's the large block moves, at the end of the N×log(N) spectrum. Small blocks are fine but if they grow, the high-level, end-of-sort merges become... heavy. Hashing data can help with this issue, so we can work with "small" blocks of around 100 to 1000 items each. Maybe 256 is the sweet spot. This way, no fear to spend a lot of time managing big blocks at the end of the sort. And it's possible to merge several blocks at a time, in both directions, right ? So let's consider a 2×4 merge operation for later. But we have to start somewhere.

For now I'm back to the "simpler" algo which uses a dual-purpose stack at the top of the main area.

Has anybody merged runs from both ends ?

...

Merge sort is traditionally done from one end (usually the low one) to the other. But what can prevent us from doing it from both ends ?

The code is longer, sure, but modern OOOx processors have incredibly large windows of execution with more than a hundred instructions "in flight" at the same time so managing both ends at the same time would help "parallelise"  the execution and the only time both ends must re-sync is when they reach the middle of the output buffer.

Instant 2x speedup with little algorithmic change, who could refuse ?

.

.

.

Edit:

OK I see a situation where this would create problems : with runs of equal data so this is a special case to take into account.

YAMS started like another classic sort algo but it is slowly moving away from the sorting crowd, in particular after I wrote the Project Details that links it to the #PEAC project.

The original idea was derived from the standard data organisation with a "main playing field" and an auxiliary dual-purpose stack. See below.

But writing the project description made me realise that it was not really adapted to how I would use the algo and organise the data to process PEAC data. In short: as a reordering buffer.

So in the ideal case I have a dripping stream of numbers that must be sent to 2 output streams, one ordered by one key with quite a lot of locality (but not perfectly in order due to wildly varying computation times), the order with a different key that is randomly spread all across the possible range. So these are 2 different strategies though hopefully a single algo would work well enough.

The first big departure is to get rid of the traditional data organisation ("you get a whole buffer already filled with data and you shuffle them in place") and simply consider that each buffer has a predetermined size (constrained by available RAM) that is progressively filled by data in random order. So this would be some kind of insertion sort ?

One interesting characteristic of the data generated by PEAC is that all keys are different, but I don't want to rely on this. In a special case, the equality test could be a "canary", a hint that something wrong happened upstream. But this is not the subject here.

So I have a "reorder buffer" for each of the 256 chunks of my data, let's say 16MB per chunk. It gets progressively filled by incoming data in a more-or-less random order.

The first idea is to merge the "playing field" with the stack space, noting that if a looooong run was stacked before being copied to the main field, it would fill either one of the buffers yet leave one half of the total space unused. So the new hybrid organisation would have a "heap-stack"-like organisation, with the incoming/reordering stack at the top of the space, growing down, and the main playing field (or bulk of the data) at the bottom, the first addresses.

Well my first example of under-use of the total space is not the best because it would work only for very long downwards/decreasing data runs, since data are aggregated from the top, and the "top" of the stack (going down) would reach the top of the highest run. At this point, the whole existing buffer would have to be flushed to make room for the new run... Or the buffer would have to be interrupted. These two things have to happen anyway because the buffer is likely to be smaller than the data to hold.

At these scales, where the whole data set spans a couple of external SSD, I'm not much concerned by the fine-tuning of the sorts and I just want to shave anything I can and go straight to the point. And the point is that now, to me, it looks a lot like... Have you ever watched DEFRAG.EXE running ?

Things like that pop up in my head...

The point is for the data to be inserted the earliest possible at the right place to limit the further moves, so how can one determine this supposed place ? A hash table now appears in my mind, directly indexed by the key. The merge idea totally jumps out of the window for now, at least for the low-level reorganisation. But this ensures, unlike the stack idea, that there will be few small mergers for random data, and this would be directly proportional to the size of the buffer. Good bye stack !

The whole range of the keys can then be bucketted to death, with as many sub-hashes as necessary to prevent cascading effects from one bucket to another, when a bucket becomes congested. When the time comes to dump them as they are too annoying to optimise (above 50% fill) each bucket gets "coalesced" (all the entries are successive entries by removing the empty spaces, this is O(n) operations) then the coalesced block is written to disk consecutively with the previous sub-hash. If a whole dump can manage runs of at least 1GB each time, it's a pretty effective strategy for PEAC scanning.

The "sort" needs to know how many bits are used by the key, then how many key bits index the hash table number, then the key bits for the given hash... I want to keep the sub-hashes, or "buckets", small to ease management and keep the algo simple and fast, because now the problem has shifted to a "collision avoidance and mitigation" strategy. This also helps with input data with a narrow range. The merge itself is now pushed to a later stage when the data sink will open and read many files that are locally sorted.

Damnit, the more I write, the more the whole original thing falls apart.

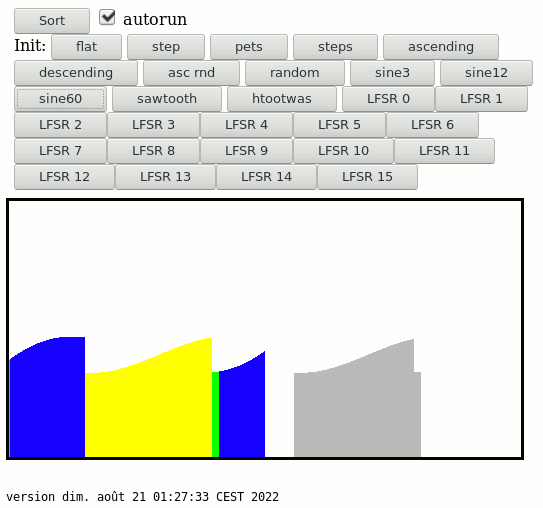
Today, Thursday 2022/8/18, I created the project and uploaded the first file sort_20220818.html.txt which contains some basic code for testing the algorithm.

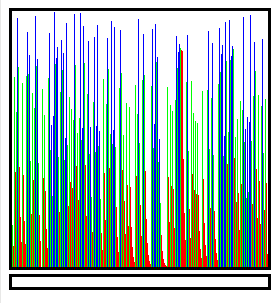
There is a crude "waveform generator" that proved precious because it showed early problems with my run-detection algorithm.

In this example, the start of the down-slope would stutter, because there are many small runs of equal values. Here I represent the "undefined slope" with green bars, while the algorithm has not found an upwards or downwards slope. This greatly reduces the number of small runs at the cost of stability but this is not a concern for my applications.

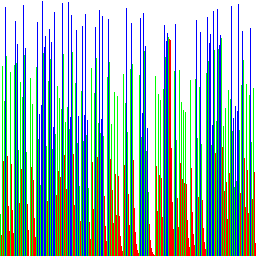
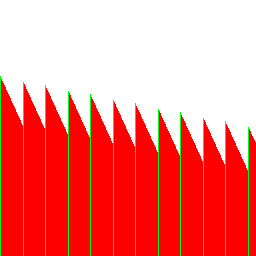
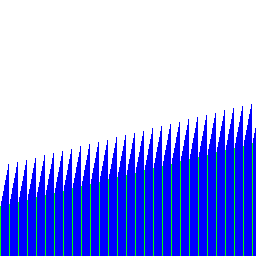
The rest of the test cases seem to work as expected:

The effect of this slope-finding code is that runs have at least 2 data, unless this is the very last item in the input stream.

There is some code to manage a stack, now I have to find the best way to use it...