La logique des équivalence repose sur une triple inversion.
- Inversion de l'operateur.
- inversion des opérandes.
- inversion du résultats.
Ce qui nous donne une table d'équivalence.
| A & B | !(_A | _B ) |
| _A & B | !(A | _B) |
| !(_A | B) | A & _B |
| A ^ B | _A ^ _B |
| A | B | !(_A & _B) |
| !(A | B) | _A & _B |
| !(A ^ B) = | A ^ _B = !(_A ^ _B) |
| _A | B | !(A & _B) |
| !(_A & B) | A | _B |
| !(A & B) | _A | _B |
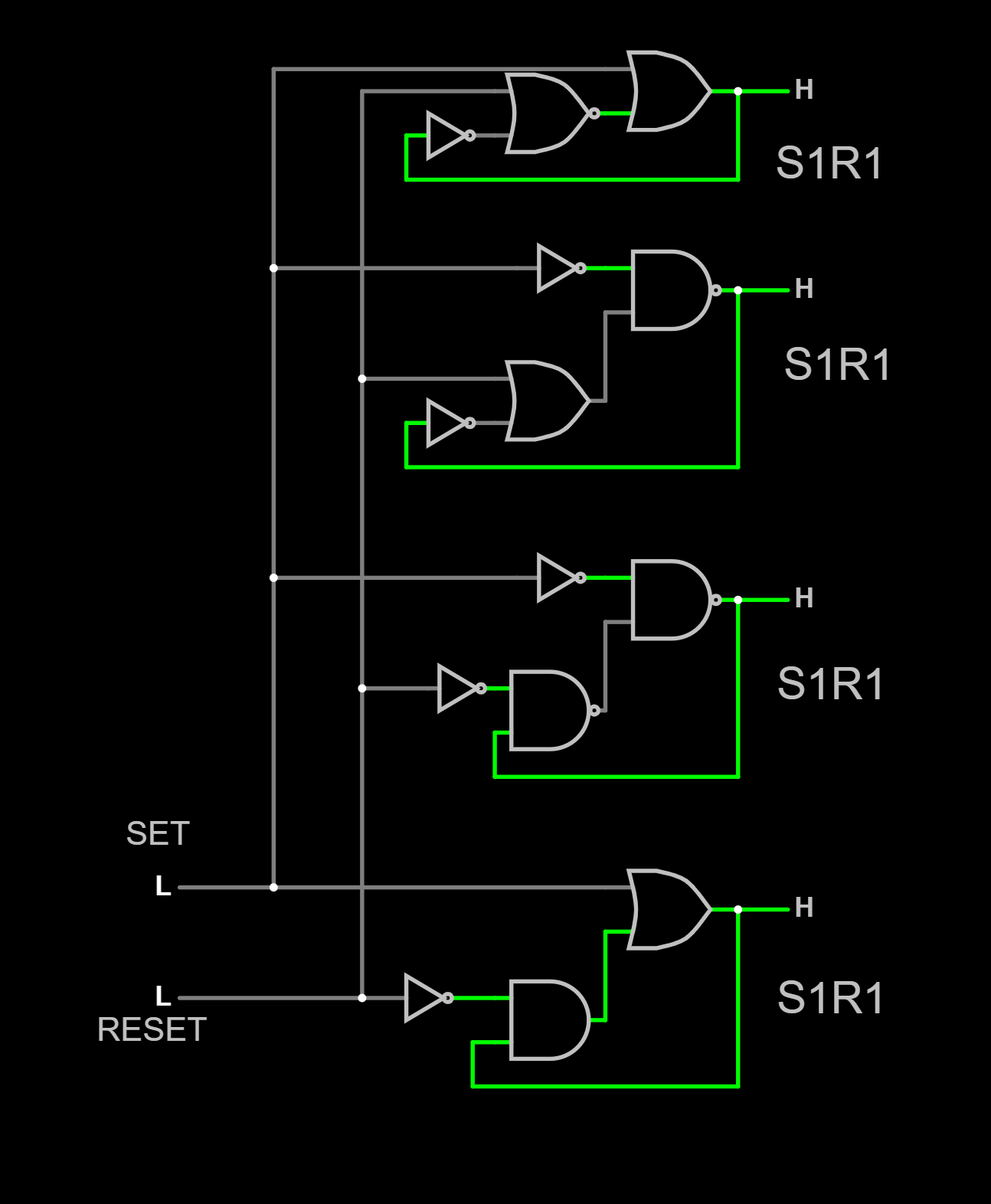
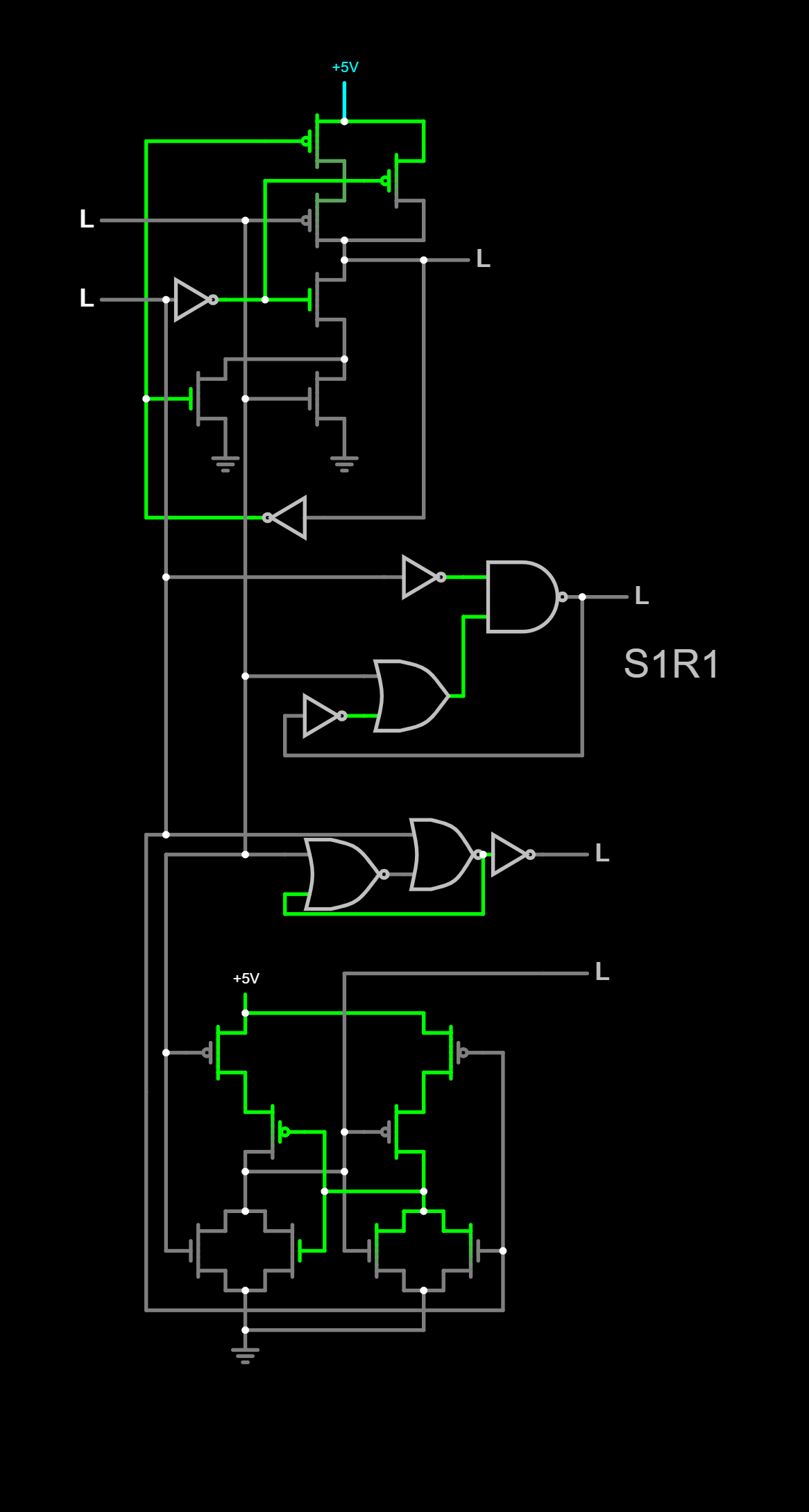
A l'aide de cette table, ou de ces règles,
L'on peux inverser des suites de portes logiques, afin qu'elles correspondent.
Cela sans avoir la même structure, ou architecture interne.
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
"!(A ^ B) = (_A ^ _B)"
hmmmm I disagree on this one, unless there is a syntax trick I missed.
Are you sure? yes | no
thanks !
its modified !
Are you sure? yes | no