To make the experience fit your profile, pick a username and tell us what interests you.
We found and based on your interests.
Pour suivre et compléter le MUX2 standard,
Voici une étude de topologie de multiplexeur optimisé, et capable d'être générer récursivement.
Ceci en optimisant le nombre de transistor utilisé !
Mais en gardant le même défaut sur la profondeur Tmax...
Cependant ces multiplexeur peuvent être pipeliné (découpé par étape chacune mise en buffer).
Le décodage s'effectue donc en 2 partie, et il encercle les inputs !
A comparaison :
L'on constate donc sur un mux 4 une économie de 2 transistor (le tier).
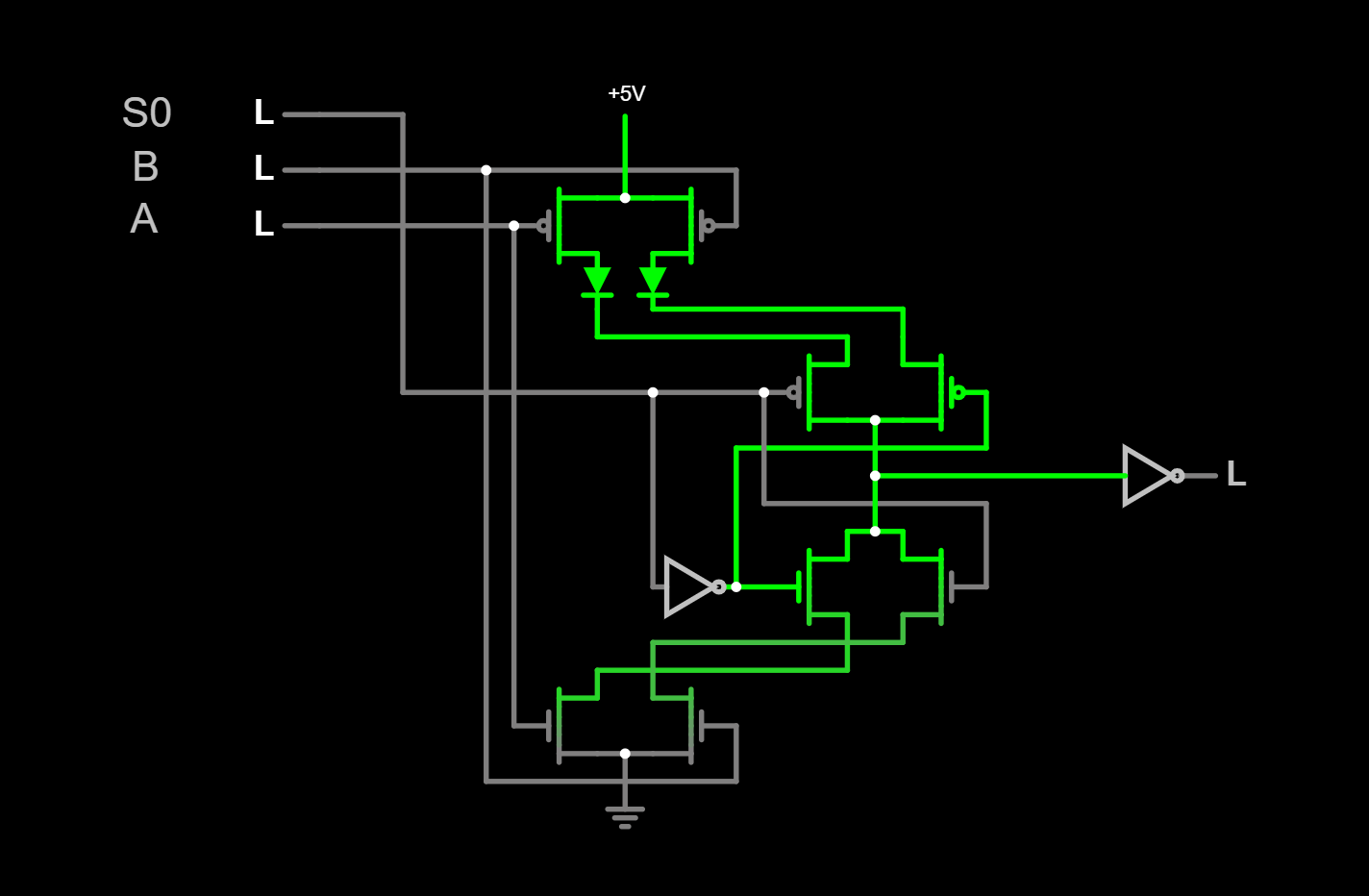
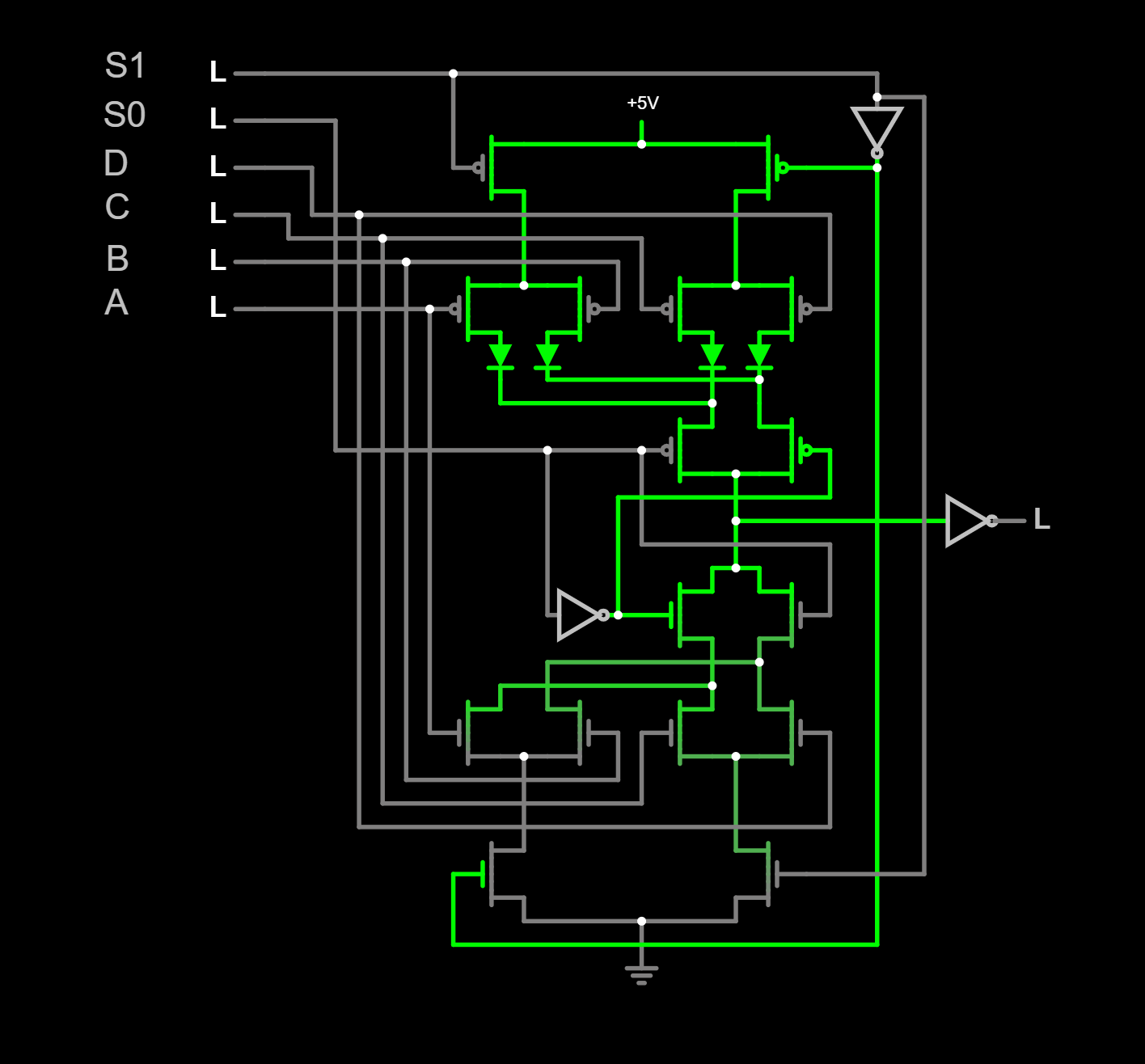
MUX16
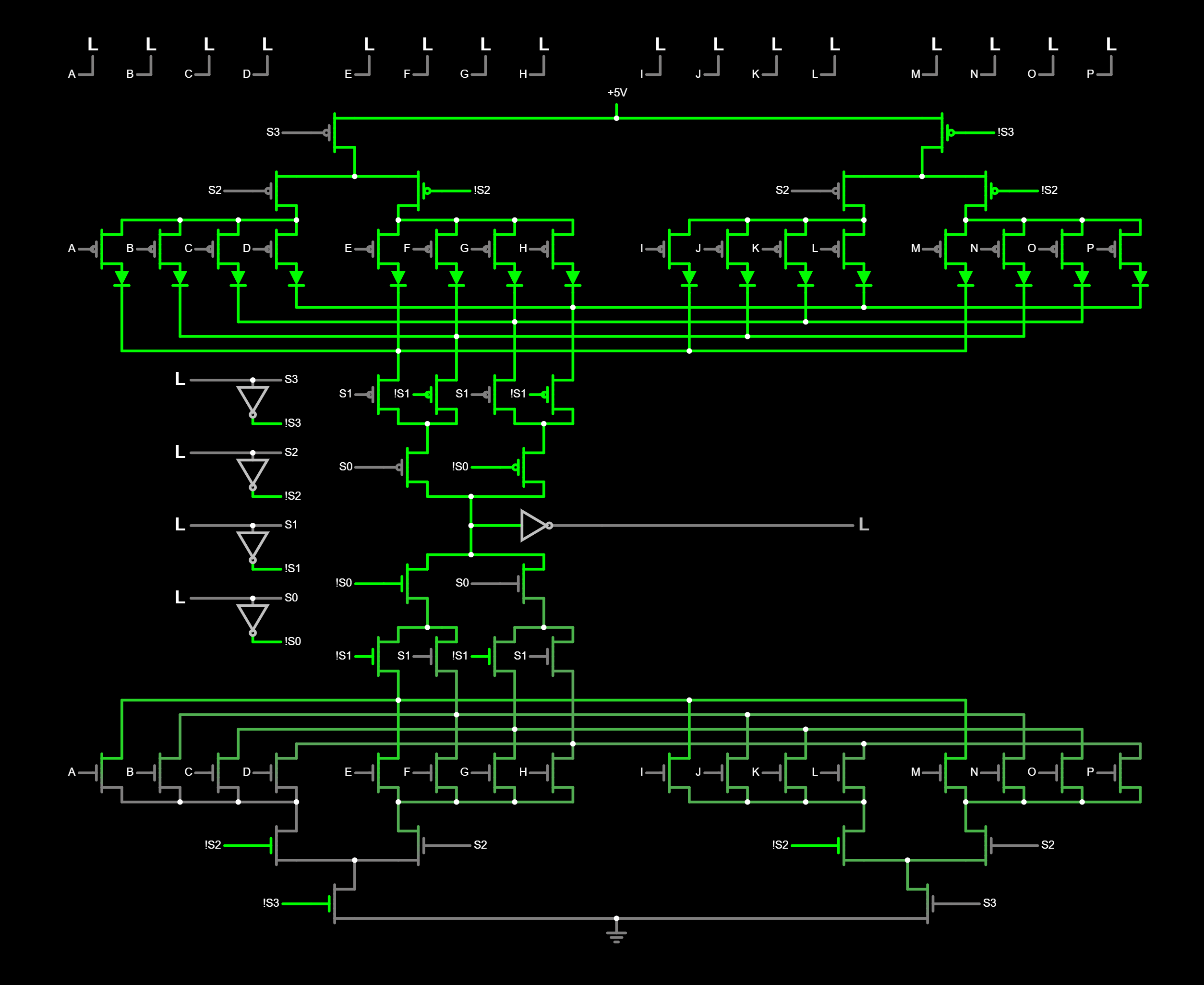
Ce que l'on remarque :
Concernant les connections entre les inputs et les entrées de control, l'on peux voir qu'il y a une connexion "en 2D".
Cela est mieux visible sur les multiplexeur plus gros.
Il existe cependant un défaut majeur... (mux4 et plus !)
Les diodes anti-retour sont obligatoire !
Sans quoi le courant sortant du drain du Pmos actif,
entrerais dans un autre depuis le "drain",
atterrissant dans la "source" d'un autre et ressortant par le "drain" de ce dernier provoquant un court-circuit !
La porte OU Exclusif est une sacrée histoire, comme on peut le voir sur ce petit bestiaire de topologies de XOR. Les configurations possibles sont multiples, selon les contraintes de fan-in et de fan-out. Des configurations à faible nombre de transistors existent mais reposent sur des transistors dont on peut contrôler les ratios donc les résistances, et jouent sur les rapports de transconductance, donc la consommation statique n'est pas insignifiante. On trouve aussi plein de versions sur https://www.vlsitechnology.org/html/cells/vsclib013/xor2.html.
Pour le cas ci-dessous, tous les transistors sont considérés comme ayant le même ratio, ce qui permet à la cellule d'être portable sur un maximum de technologies et PDK.
Pour un fan-in de 1 et fanout acceptable, on s'en sort avec 10 transistors:
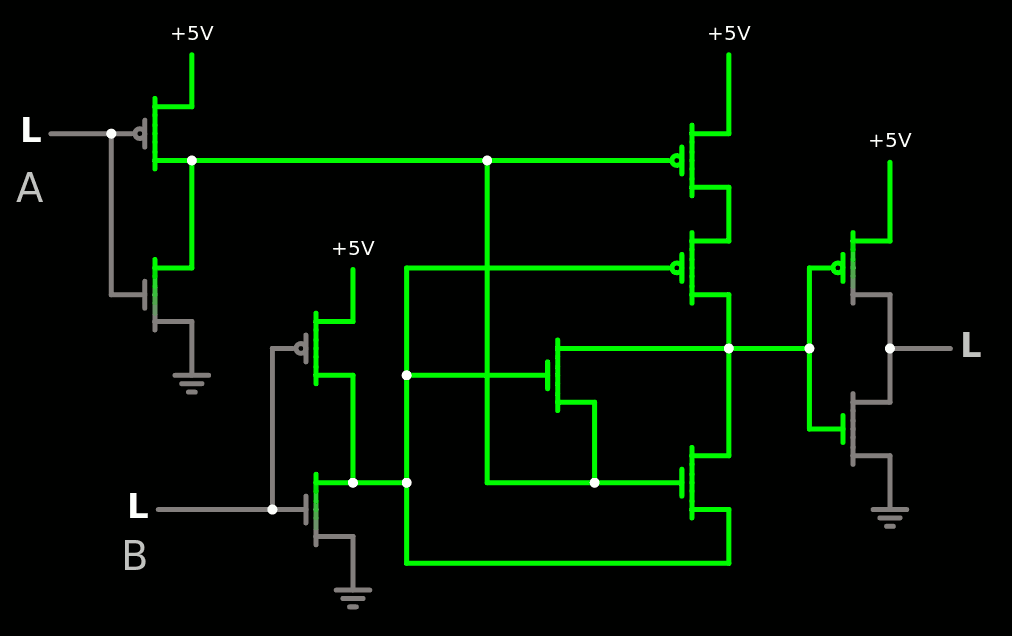
Les inverseurs d'entrée et de sortie ne sont pas optionnels, à moins que la cellule soit connectée directement à une cellule voisine dotée d'un inverseur de sortie. On pourrait faire une version XNOR avec un faible fanout en enlevant l'inverseur de sortie.
La porte XOR est essentielle à l'addition mais une autre se retrouve beaucoup dans un "carry lookahead adder" lorsqu'il n'est pas possible de fabriquer une carry chain optimisée. C'est une macro-cellule appelée CLA3 dans les projets #YGREC8 et #LibreGates.
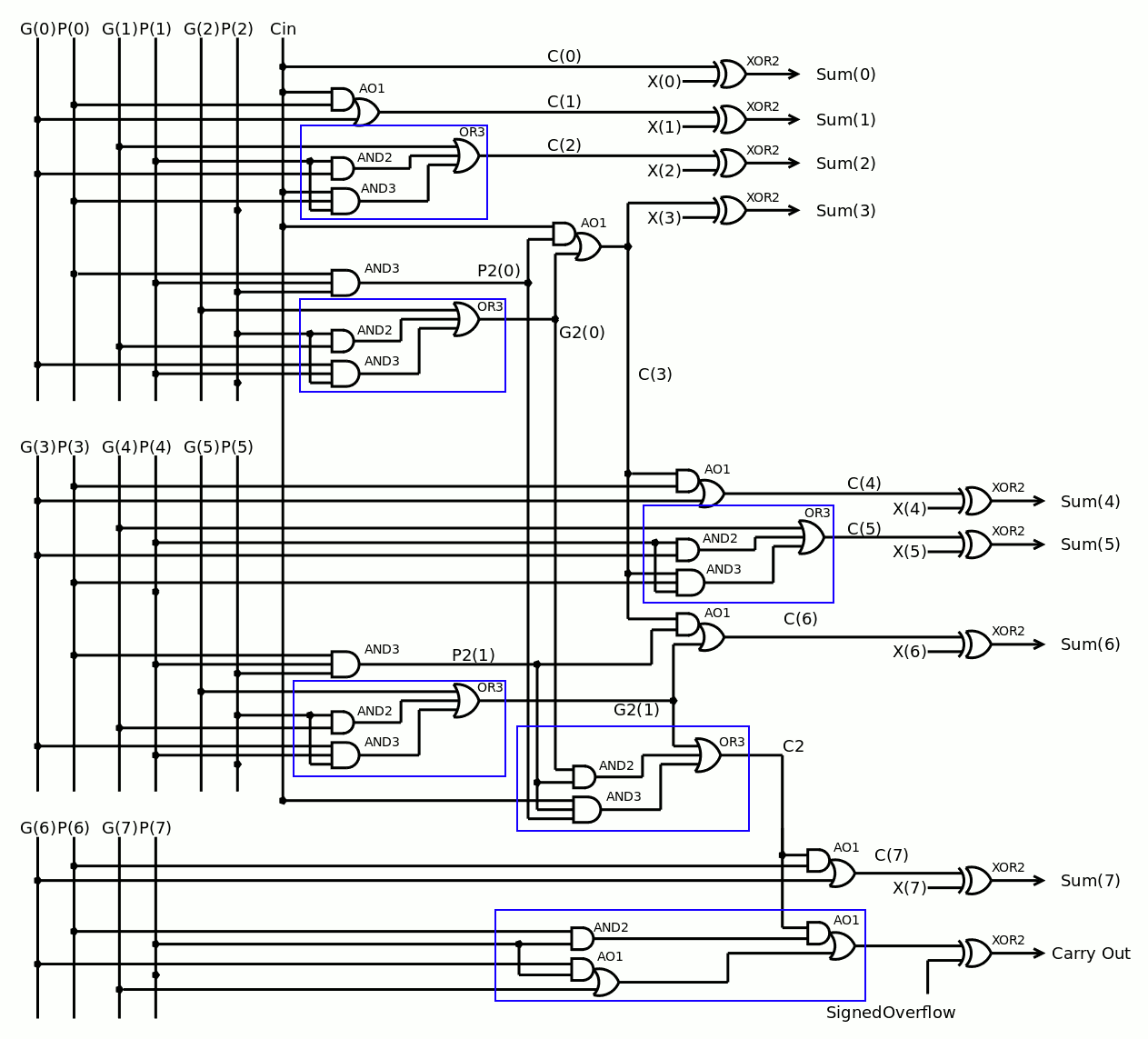
Ce circuit a été optimisé pour travailler avec des portes logiques à 3 entrées et les signaux Propagate et Generate sont décrits autre séparément, intégrés dans l'unité logique/ROP2.
Il y a déjà 6 unités CLA3 dans un additionneur 8 bits donc c'est un bon candidat pour une optimisation. Nous pouvons partir du circuit présenté dans le log Expansion des portes logique en cmos en modifiant le circuit aoai_3_2_1.
Cela donne le circuit suivant :
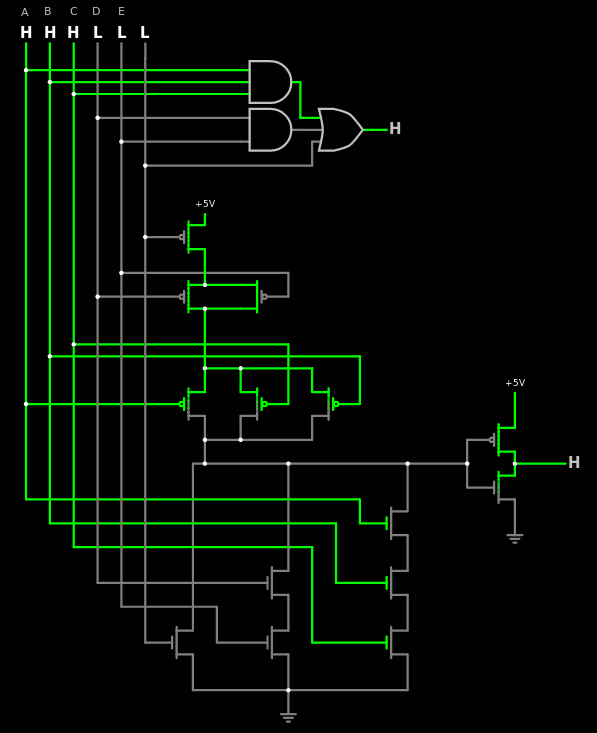
À partir de là il suffit de mettre une entrée en commun, ce qui se simplifie avec une petite modification de la topologie des transistors.
Cela donne ce circuit un peu plus petit :
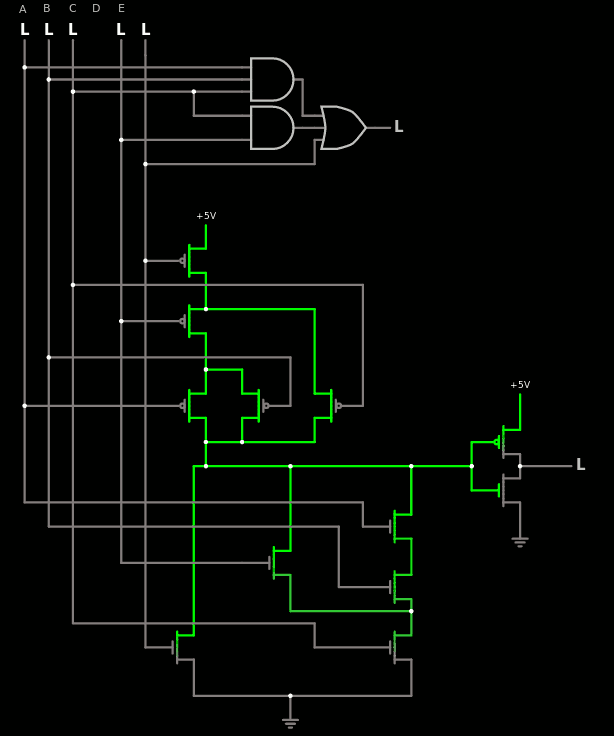
Cette version contient 12 transistors, dont 2 pour l'inverseur en sortie, ce qui lui permet d'attaquer un fanout de 2 ou 3 sans difficulté. Cependant dans deux cas sur le schéma du début, la sortie attaque une seule entrée donc une autre version sans inverseur est possible (ce qui donne CLA3I). En aval, il faut alors faire du "bubble push".
Après discussions, le MUX2 est ainsi:
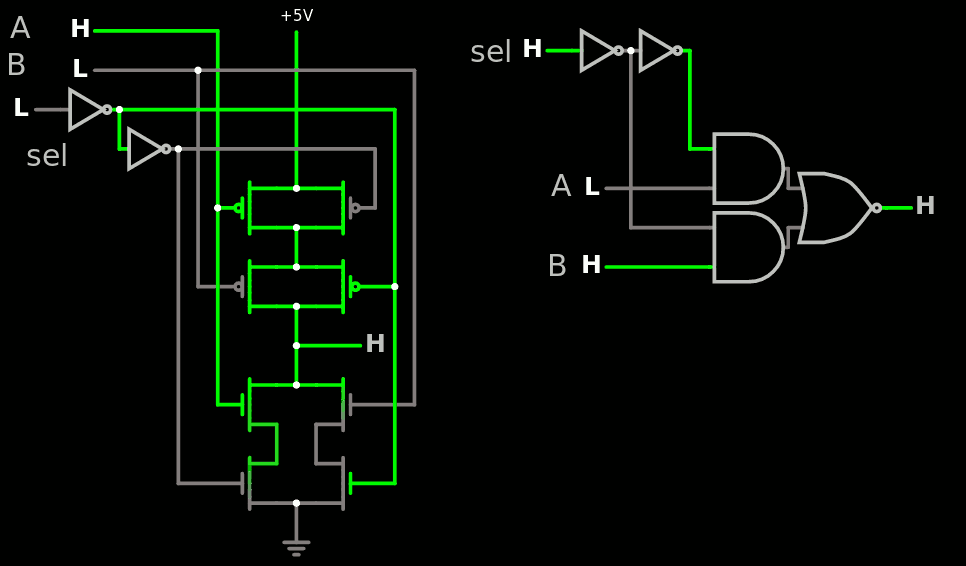
La porte logique équivalente est assez évidente, la seule question concerne les inverseurs. J'en ai mis 2 en entrée pour 2 raisons :
* réduire le fan-in, puisque ce genre de signal vient souvent d'un nœud distribué sur beaucoup d'autres portes,
* redresser le front du signal entrant et réduire le temps de transition, pour réduire la consommation dûe aux transconductions transitoires.
En fait on voit ici un MUX2I et pas un MUX2, car l'inverseur en sortie est optionnel, selon l'usage : si la sortie va directement sur une autre cellule voisine, ce n'est pas requis, mais dès qu'il y a un peu de distance, cela devient nécessaire. Donc 2 versions sont possibles.
Si les inverseurs en entrée ne sont pas nécessaires (pour réduire la taille, ou parce que des signaux complémentaires sont déjà disponibles autre part) alors on peut réutiliser la porte logique de base AndAndOr.
Le log Expansion des portes logique en cmos a dégagé plusieurs règles de construction, qui s'ajoutent à la métrique FO4.
Cependant dans une implémentation physique il existe un paramètre supplémentaire : la profondeur maximale des transistors, ou le nombre de transistors qu'on peut mettre en série.
C'est une conséquence du fait que chaque transistor a une résistance à l'état passant. Cette résistance affecte la performance et mène a des compromis entre :
En suivant la règle t=RC, augmenter la résistance diminue la fréquence de fonctionnement. il devient donc nécessaire de définir le nombre maximal de transistors, "Tmax", admis en série.
Pour cela nous allons utiliser une matrice de cmos, car ce qui se trouve en série en haut, se trouve en parallèle en bas !
Ainsi une complexité Tmax = 1, est un inverseur (1x1).
Pour Tmax=2, cela donne une porte à 4 entrées (2x2)
Matrice que l'on peux ensuite élaguer pour donner une NAND ou une NOR simple.
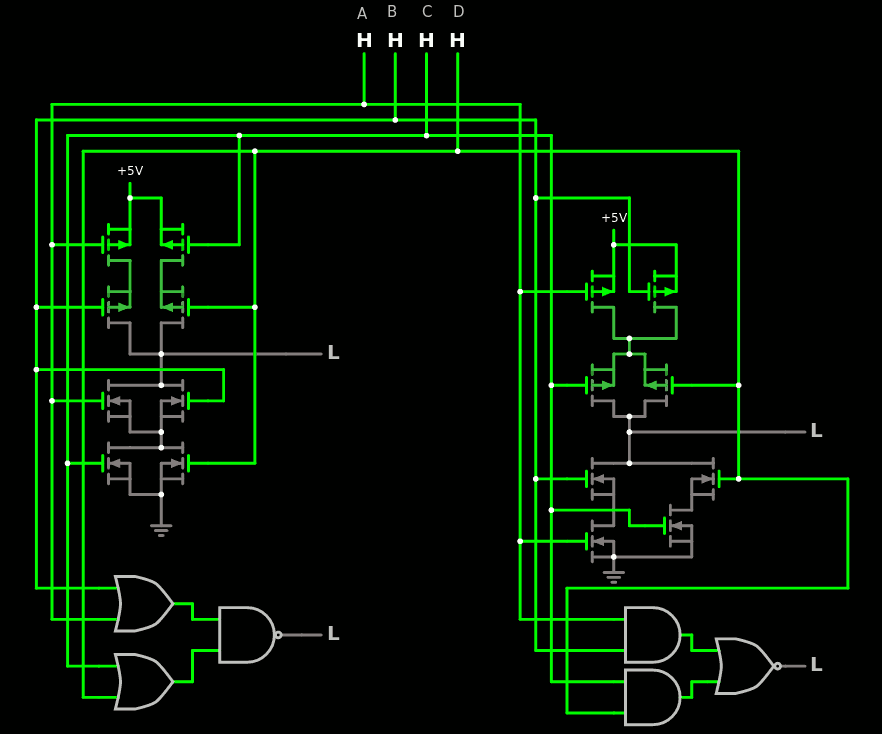
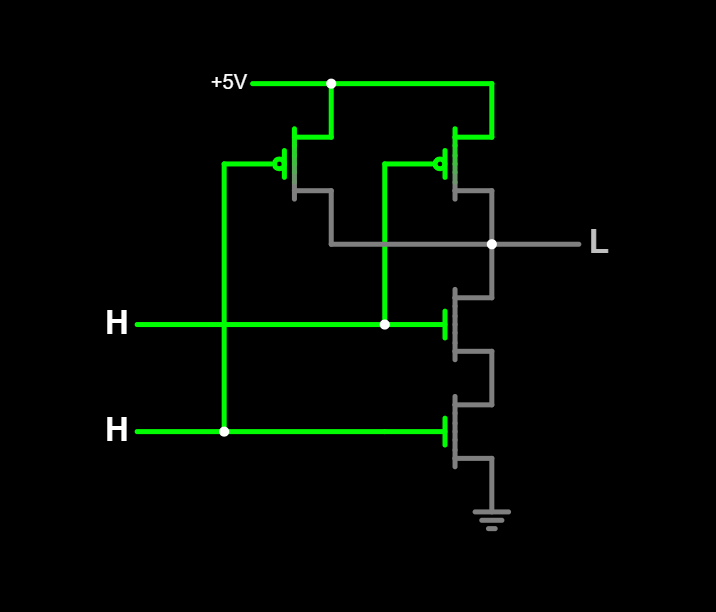
Tmax=3 donne un bon compromis en terme de complexité et de complexité de routage, si on limite le nombre d'entrées, car ce dernier peut monter à 3×3=9.
Ces configurations "maximales" ont deux avantages :
L'utilisation de profondeurs plus grandes a un avantage si cela permet de réduire la profondeur logique du circuit (le nombre de nœuds d'inversion traversés pas une entrée vers la sortie).
Par exemple,
Un OR4 prendra moins de place et peut-être un peu moins de temps que deux 0R2 en série. Mais les fronts seront plus lents !
C'est en effet un compromis à trouver et à tester, en fonction des caractéristiques de la technologie.
Mais surtout, il faut aussi limiter le nombre d'entrée car sinon, la cellule correspondante devient trop grande et difficile à router.
Conduisant au débordement probable sur un autre niveau de métal.
Une limitation à 4 entrées est un bon début mais ce n'est pas une limite absolue puisque nous voyons plus haut que pour atteindre un compromis de Tmax=3, on peut monter à 9 entrées et de nombreuses portes à 5 ou 6 entrées peuvent être très utiles.
Le layout de la cellule correspondante peut devenir difficile.
Les PDK "minimalistes" (type OSU) permettent de synthétiser la plupart des circuits courants mais il est plus efficace de synthétiser les portes à la demande, en fonction du circuit.
C'est plus lourd mais la performance demande toujours plus d'efforts !
La logique des équivalence repose sur une triple inversion.
Ce qui nous donne une table d'équivalence.
| A & B | !(_A | _B ) |
| _A & B | !(A | _B) |
| !(_A | B) | A & _B |
| A ^ B | _A ^ _B |
| A | B | !(_A & _B) |
| !(A | B) | _A & _B |
| !(A ^ B) = | A ^ _B = !(_A ^ _B) |
| _A | B | !(A & _B) |
| !(_A & B) | A | _B |
| !(A & B) | _A | _B |
A l'aide de cette table, ou de ces règles,
L'on peux inverser des suites de portes logiques, afin qu'elles correspondent.
Cela sans avoir la même structure, ou architecture interne.
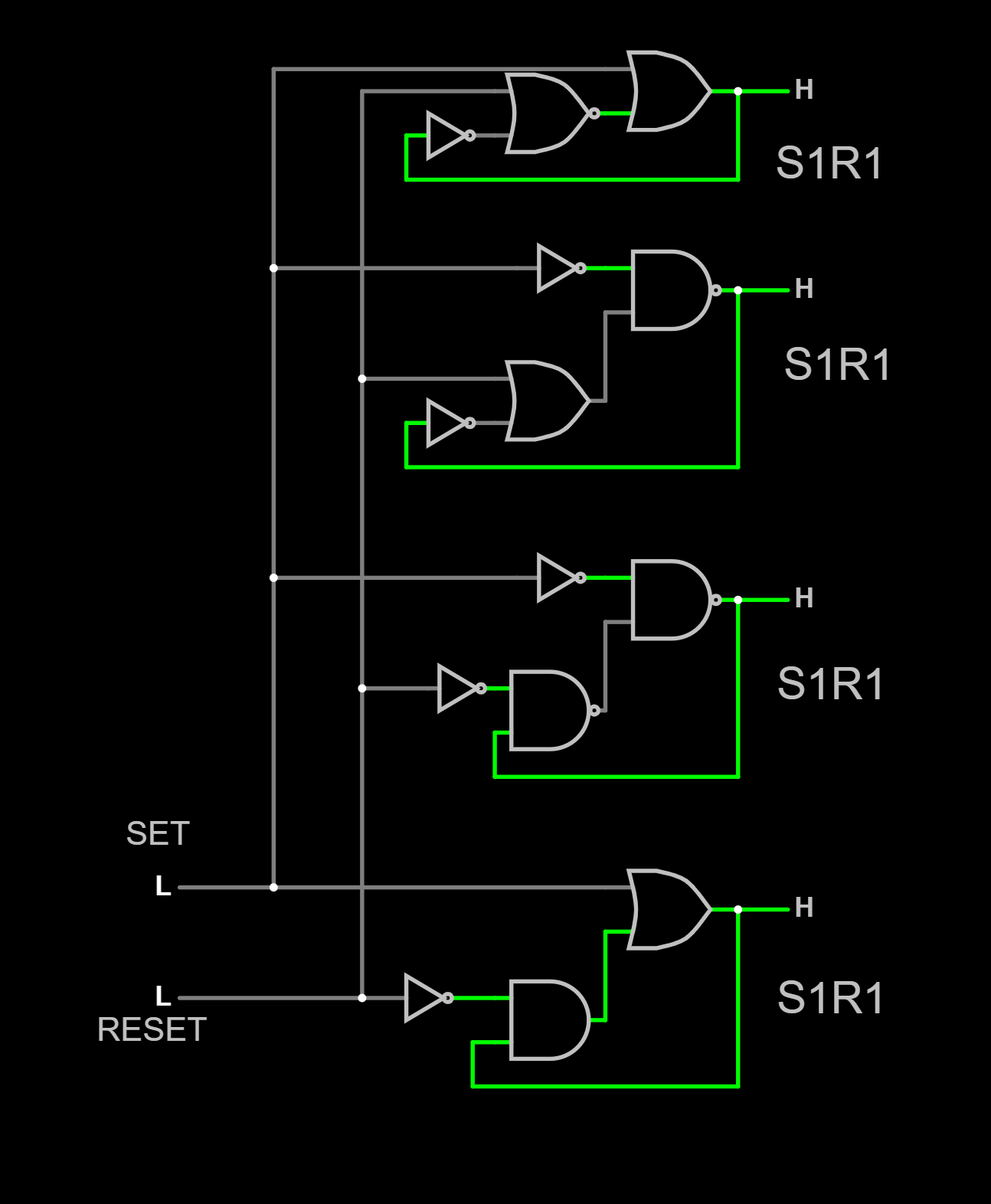
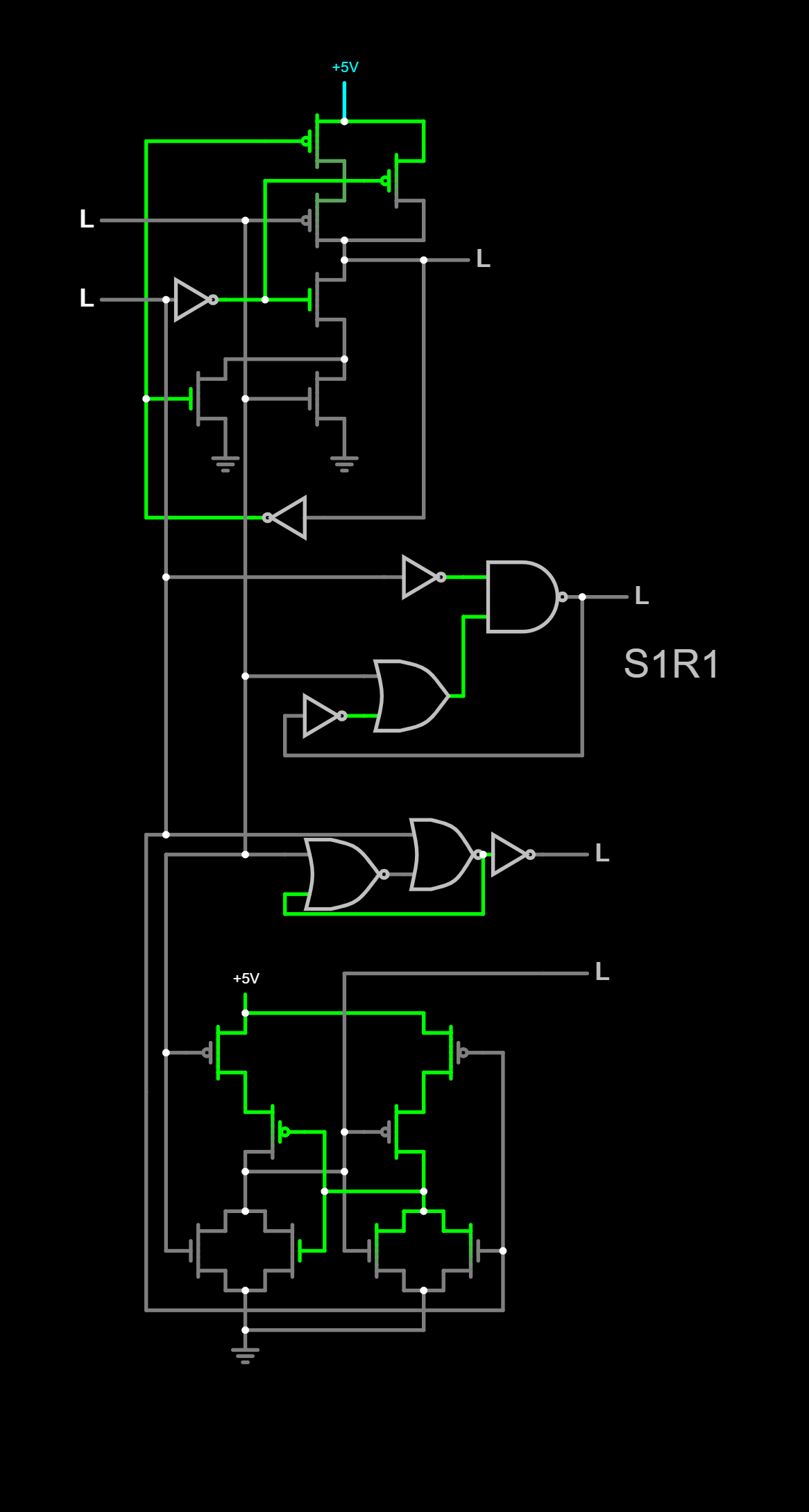
| nand2 -> nand3 | ! (A & B) | ! (A & B & C) |
Depuis nand2 on ajoute :
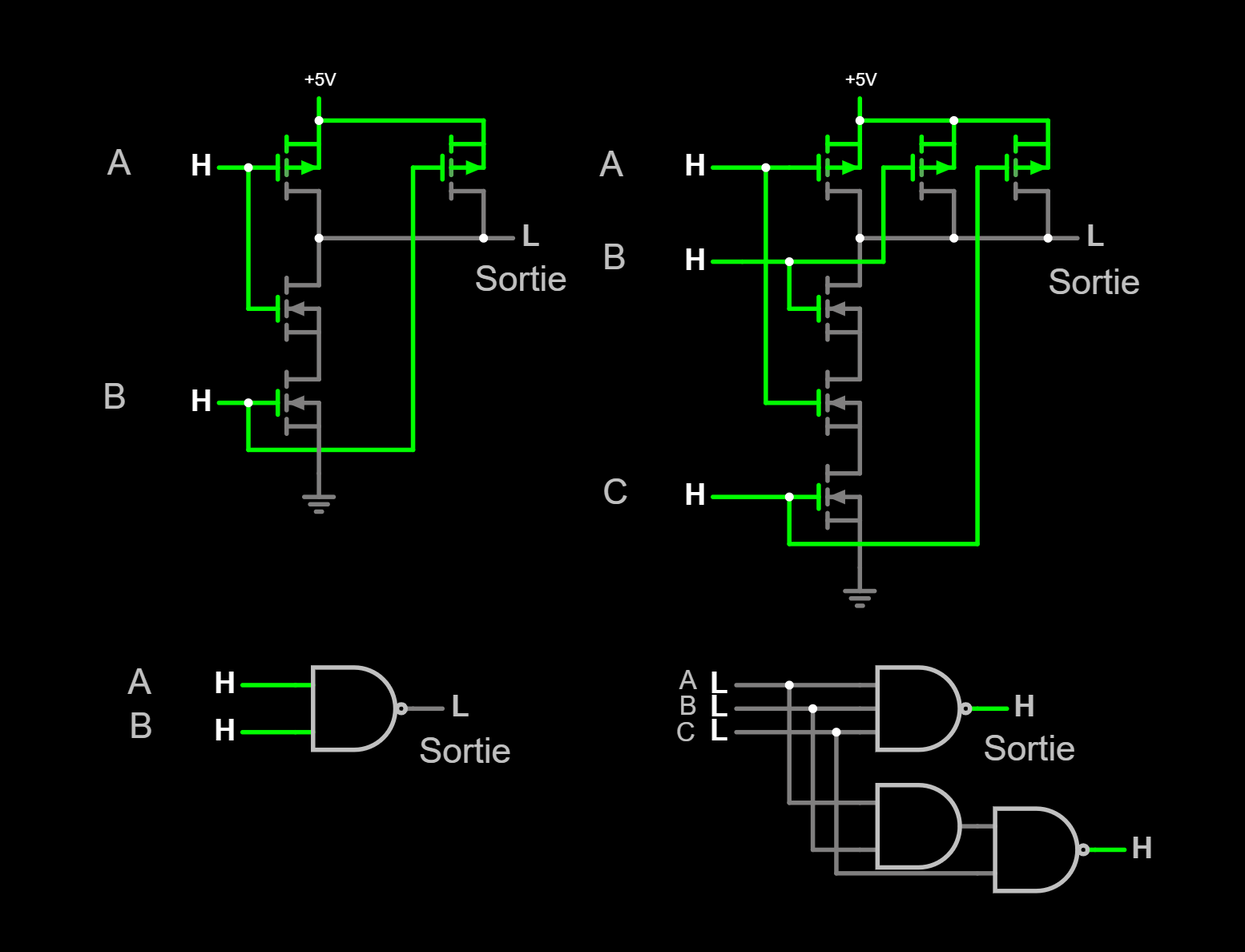
| nand3 -> aoi_2_1 | X = (A & B) !(X | C) |
Depuis nand2 on ajoute :
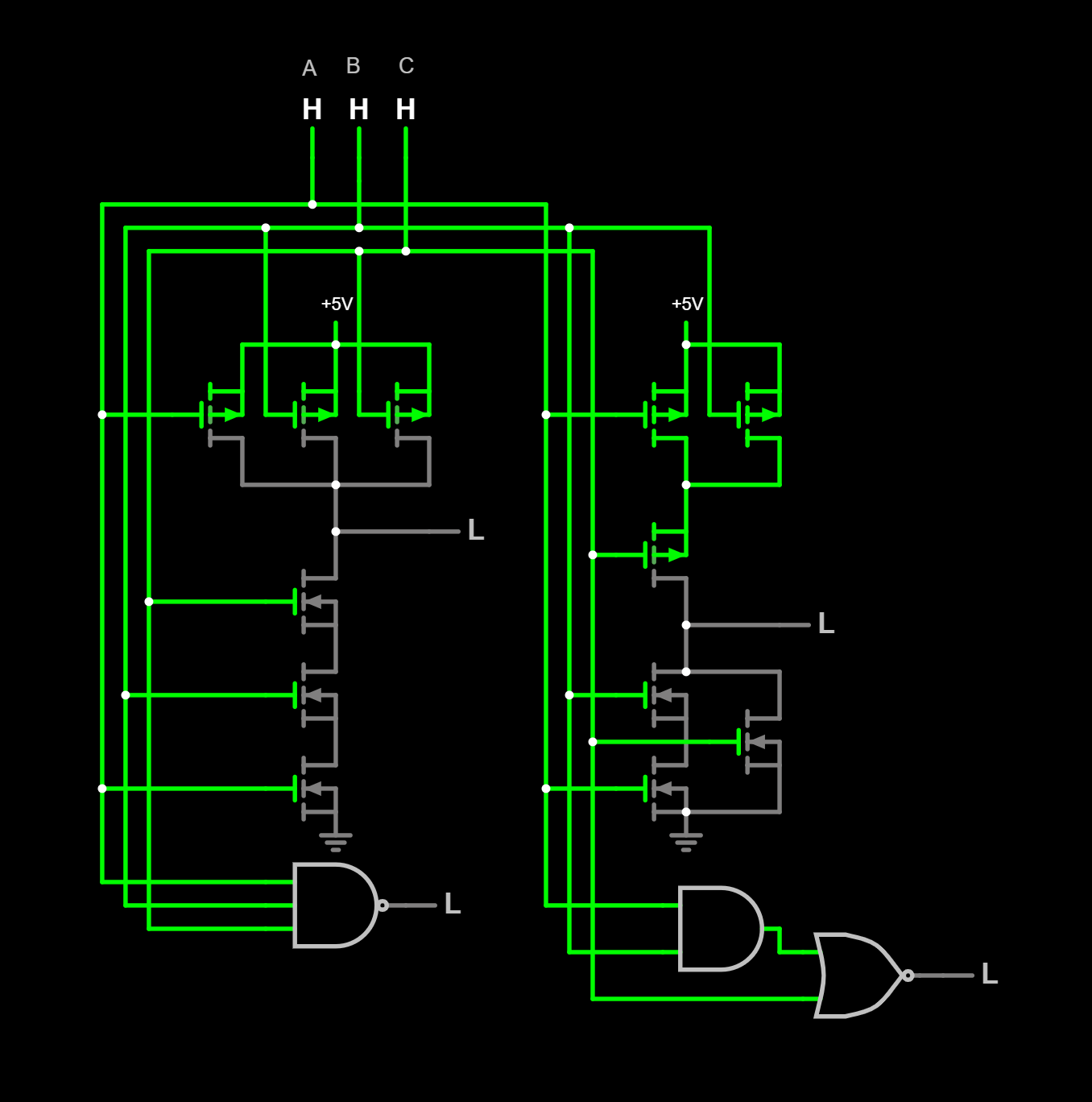
| nand3 -> aoi_2_1 -> aoi_2_2 | X = (A & B) Y = (C & D) ! (X | Y) |
Depuis nand2 on ajoute :
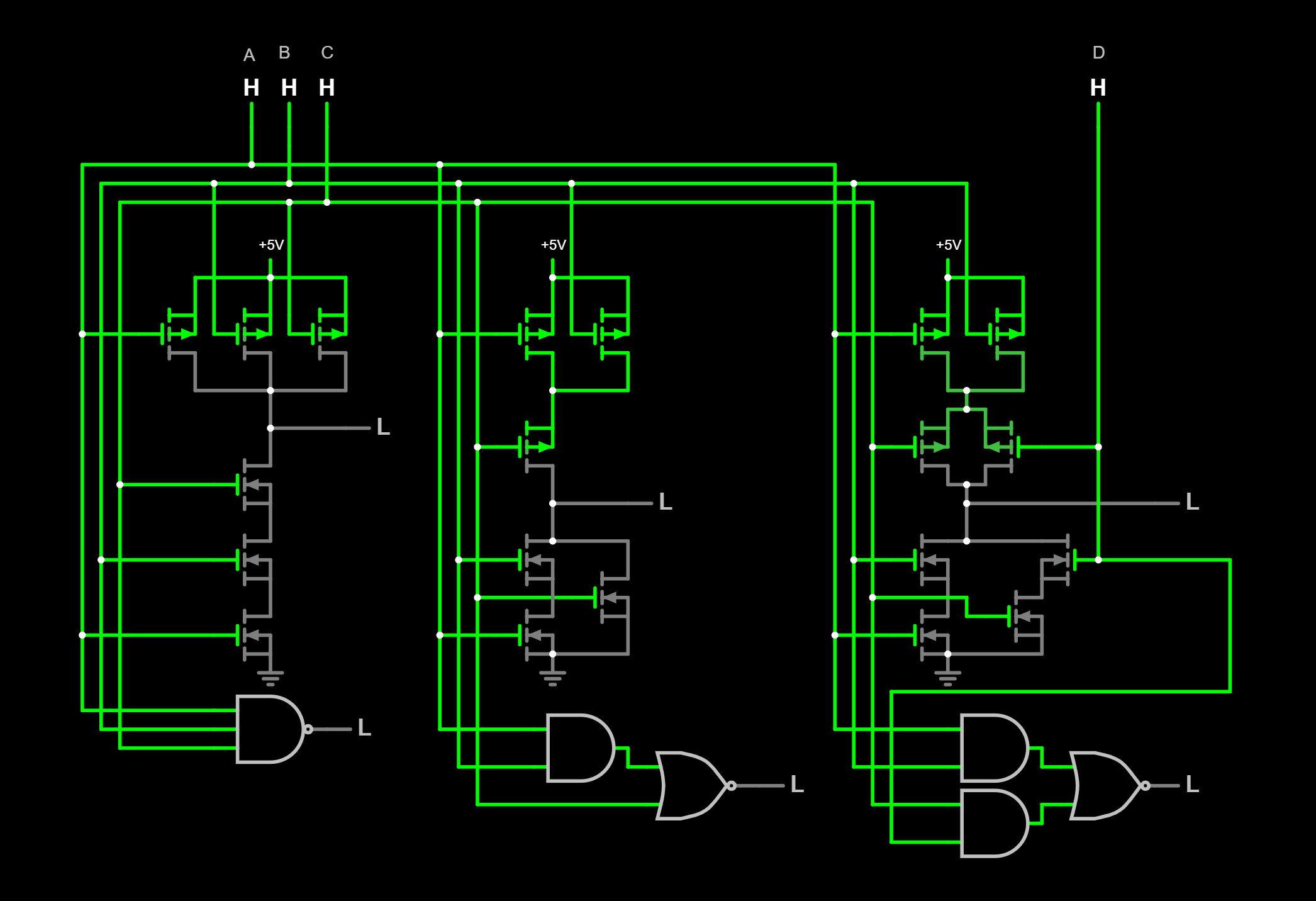
| aoai_3_2_1 | X = (A & B & C) Y = (D & E) Z = ( X | Y) ! ( Z & F) |
Ce circuit contient :
| mixed_NAND |
Ce circuit contient :
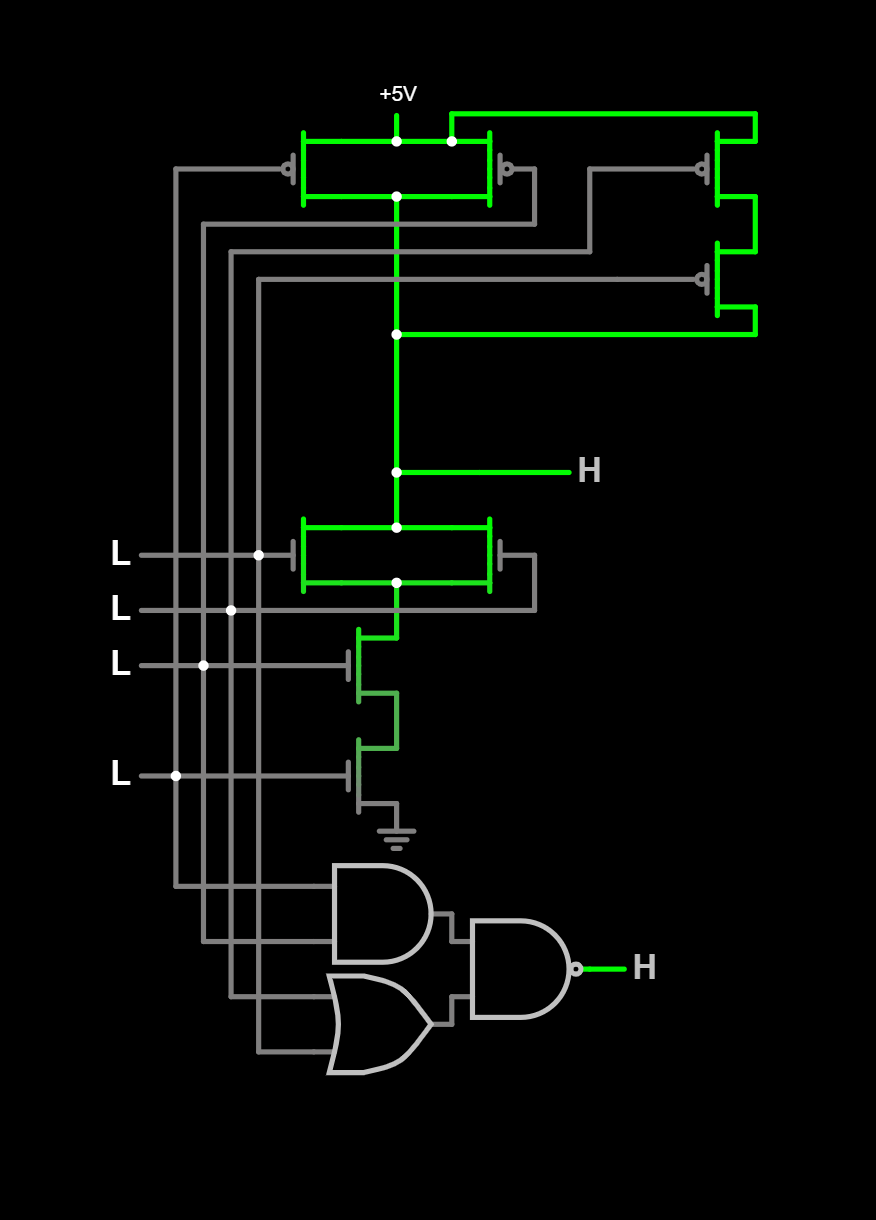
| mixed_NOR |
Et on inverse mixed_NAND !
Ce circuit contient :
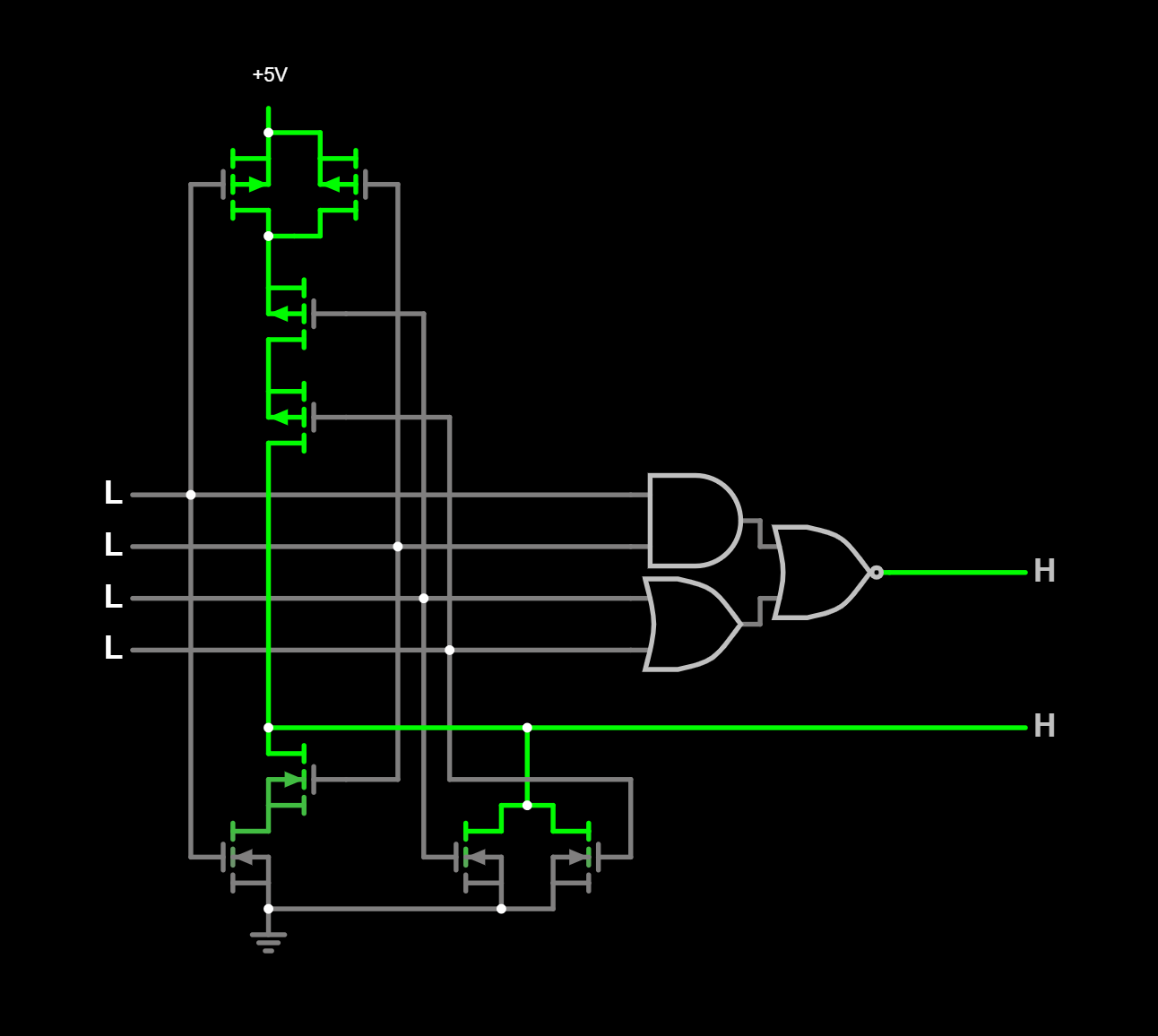
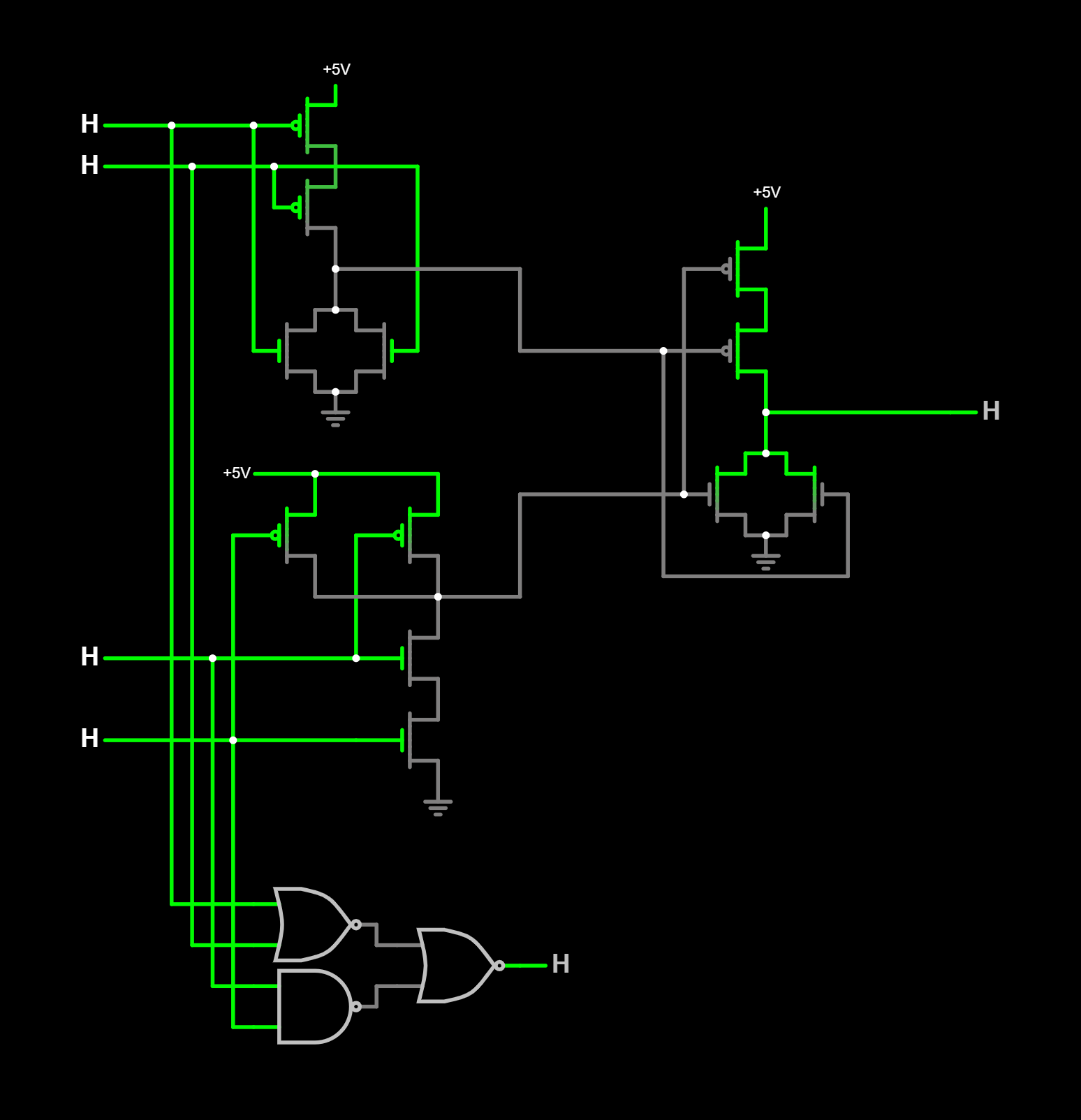
Constat :
Create an account to leave a comment. Already have an account? Log In.
Become a member to follow this project and never miss any updates
 plopez
plopez
 llo
llo
 Brian Wyld
Brian Wyld
 Victor Sepulveda
Victor Sepulveda