Narcissus 12.0

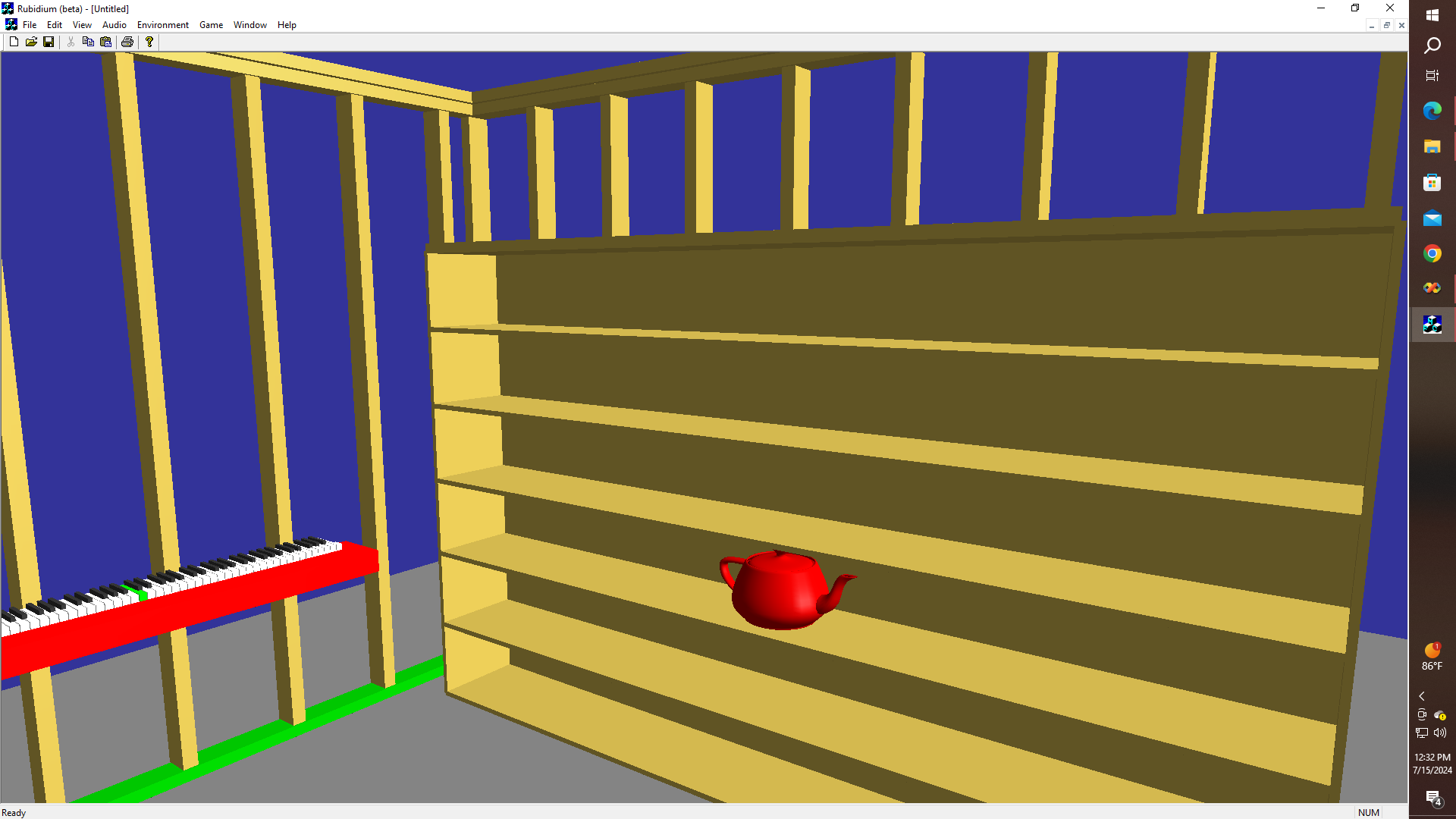
As I see it, if LAME is an acronym for "Lame isn't an MP3 Decoder", and if GNU is an acronym for "GNU is not UNIX", then what might JADE stand for?  How about "Jade isn't Just Another Doom Engine" either?  And it isn't another Doom engine yet, in any case.  But at least I am starting to be able to stockpile my bookshelf, with teapots and things.  Maybe adding some plywood sheathing or a nice brick facade to the exterior of those walls wouldn't be such a bad idea either., along with a nice interior finish, of course.  And never mind the fact that most of the western United States is experiencing a thousand-year drought; a nice green lawn is going to be another "must have" - and finally, as discussed in a previous post, I know how to do it.

Ever wanted to build a REAL "Tiny House" with a simple, easy, and fast floor-plan editor?  Or how about a nice bookcase that hopefully doesn't fall apart in a week?  Honestly, I find the fact that "Blender" is something like Two MILLION lines of code, kind of appalling, and while Ki-CAD is also an excellent open-source project, I am not aware of anyone using it as a game engine, or as a substitute for Auto-CAD or Vector works.

A real-world bookshelf is something that is on my to-do list, and for whatever it is worth, printing to PDF is supported in an earlier version, IIRC of what I am working on right now, i.e. in the Terminal-View, and or Signal-View classes in my Propeller Debug Terminal application that I wrote, whenever that was, I think it was 2019.  Yeah, so maybe this works in the code that is on Git?  I will have to check on that.

Of course, I still need to add DOOM support, Raspberry Pi support, and P2 support.  But architectural drawings in a standard format, and properly scaled, maybe even good enough for some building departments, just in case your Tiny House needs a permit, well - it's not that hard to do.  Or one can export the OBJ files and pull them into another program like Blender (free) or Auto-CAD ($$$$!) for additional work.

And I still want to do SHRDLU.  But in the meantime .... 

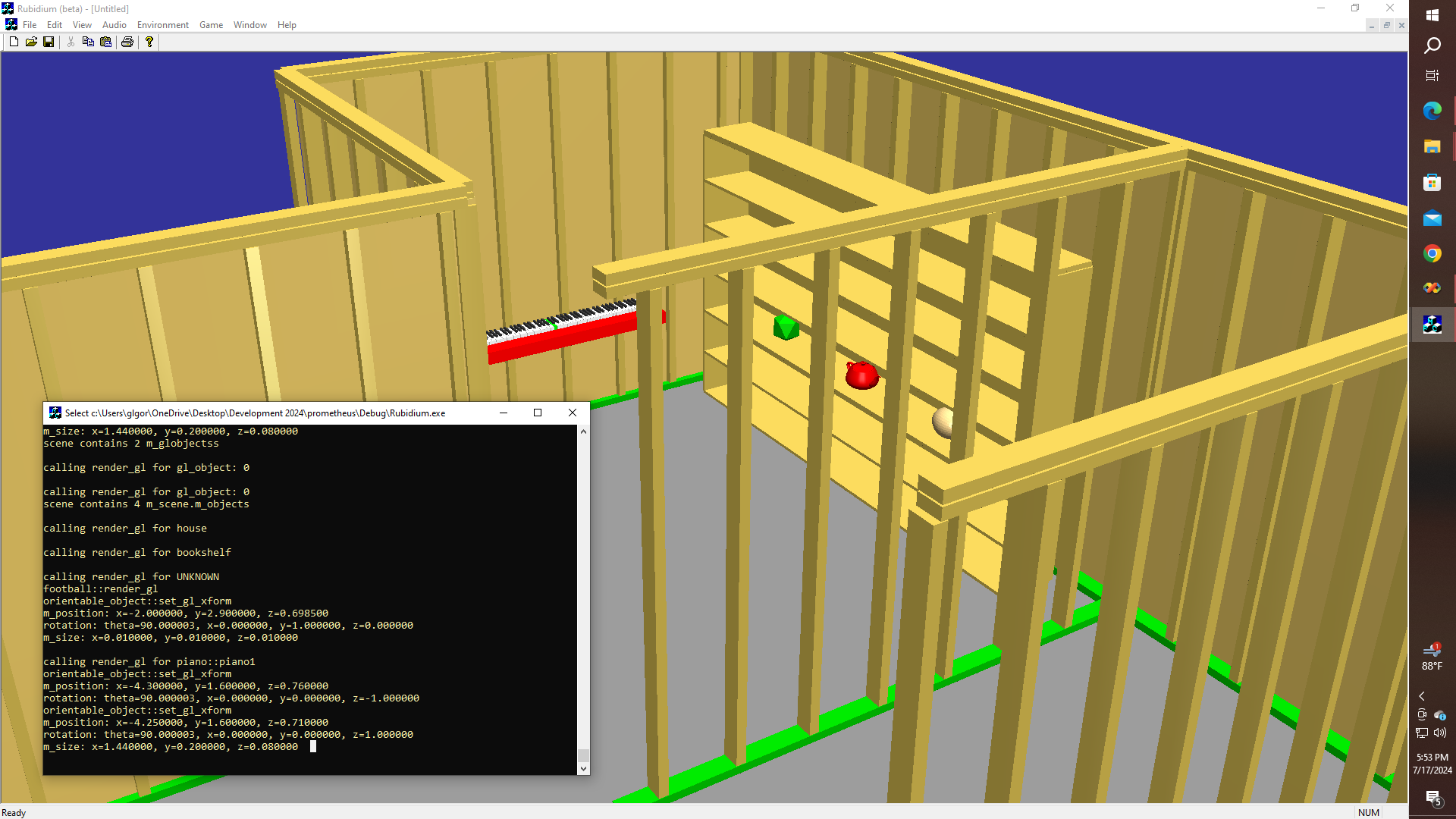
Yeah, in the "meantime", I got some more objects to render in OpenGL, and am starting to fill up the bookcase a bit more.  Also figured out how to get some sheathing up on those walls.  This means of course, that "Tiny-CAD" is very much alive, and the prospects are looking to be a lot more realistic as far as having a chance of being able to generate not just some fun game objects, but the idea of being able to, as I said, actually print out usable "working drawings" for some very useful real-world stuff.  Doors and Windows would also be nice I suppose.  Along with some electrical and plumbing maybe?  How much more complicated can it get?  Well, actually - now that I mention it, there is a method to some of the madness, that I should probably go into at some point because I figured out something quite interesting the other day while fixing up the icosahedron code, which now looks in part something like this:

icosahedron::icosahedron ()
{
    int i,j,edges;
    MATH_TYPE x,y,z,theta,phi;
    m_color = COLOR::green;
    m_vertex = &(m_vertexes[0]);
    m_vertex [0] = _vector (0,0,1);    
    m_size = _vector(1000.0,1000.0,1000.0);
    for (i=0;i<11;i++)
    {
    theta = 2*i*PI/10;
    phi = (i%2==0? PI/3:PI-PI/3);
    x = cos(theta)*sin(phi);
    y = sin(theta)*sin(phi);
    z = cos(phi);
    m_vertex [i+1] = _vector(x,y,z);
    }
    m_vertex [11] = _vector (0,0,-1);
    edges = 0;
    for (i=0;i<12;i++)
    for (j=i+1;j<12;j++)
    if (m_vertex [i].dot (m_vertex [j])>0)
    {
    m_edges [edges][0] = i;
    m_edges [edges][1] = j;
    edges ++;
    }
    size_t sz = sizeof(m_faces);
    memset (m_faces,0,sz);
    ASSERT(edges==30);
    construct_faces ();
    thing::m_gl_index = GL_OBJECTS::GL_ICOS;
}

O.K., take a look at what is happening here because I figured out how to do something that is mind-boggling.   Do you see that section where it says: if (m_vertex [i].dot (m_vertex [j])>0) and then, in effect whenever that dot product of two vertexes, (hint there are 12) is greater than zero, that is when we have a valid edge, that is to say, for the 30 possible valid combinations of two vertexes out of the 66 total permutations of pairs of vertexes.  

Next, and elsewhere, I do another test on a pair of edges, to see if they share a connection, and then and only then, if they do, I check to see if they also form a triangle, and then I generate a polygon until all 20 triangles are solved!   Weird, but it works!  And there is something cool I think about actually being able to solve for the edges and faces, and not just to simply look them up in some table as if the only way to do it was to have it all "pre-calculated"!

This gives me an idea about how to perhaps generate point clouds from photographs, let's say - and then if you can do that - why not solve for edges, faces, and therefore objects - in the more general case.  Otherwise, I don't know how the "deep-AI" people are trying to do it, even if what I am now thinking of also seems to hint at a merger of ideas, along the lines of finding the convex hull, vs. variations on the traveling salesman's problem.

What?  Were you expecting some kind of unicorn perhaps? Is it teatime yet? Or what else might be happening? I managed to get the OpenGL code working for the latest revision of the hair drawing routines, using the "Digital DNA" - approach as I described earlier. This will also work quite nicely for blades of grass, or maybe even Velcro-like materials. Love the new NVIDIA graphics!

As I said earlier, IIRC - real hair just as often as not will have an elliptic cross-section. which is one of the things that helps curly hair be curly, and so on.  This is why IMHO, using the DNA drawing code that I figured out from drawing gears is so useful.  Yet if you ever read one of my other projects, entitled "The Money Bomb!", you might remember this 3-D printed gear, which I somehow managed to print using a commercial 3-D printer on the one hand, but so also using an OBJ file that was also therefore created, nonetheless - entirely from scratch.

So, 50,000 or so lines of code later, I still can't 3-D print artificial trees for a model railroad that I will never own.  Oh well.  Maybe a nice icosahedron?  Or a golf ball?  Not sure how well that one would work out.  The idea of printing or milling at the nanoscale, whatever that might mean, does have some appeal.  Maybe.  It is so nice to have a project that otherwise does nothing in any case.   Where their final product contains no Arduino, nor any other circuitry, no batteries, no source of power.  It doesn't even need to blink.  It is sufficient for it to merely exist, at least for now.  

Attempting photo-realistic modeling of various types of hair, including curly hair, straight hair, kinky hair, as well as blades of grass, stalks of wheat or corn, etc., is not as simple as it might seem. Curly hair usually has an elliptic cross-section, making it a very useful construct to have the ability to compute the bounding rectangles for rotated ellipsoids, for example.  Then one can generate the correct meshes, to include the various twists and turns, etc., at about 1000 hairs/square inch maybe? Thus, from the wireframe, we build up the meshes, hopefully, and then it becomes possible to add textures, or at least fill in an appropriate color for each quad or triangle. Are a million triangles enough, or should I go for 10 or 100 million?  Wondering how far I can push CUDA in real-time? Suffice it to say that the GDI frame rates are abysmal, but a necessary step in the process. Then of course we will want to have braids. Of course, we must have braids!

Now I am starting to think about also getting this to run on the P2 chip, which was always my original intention; or maybe on something else, like a Commander X16, if I ever get one of those.  Some kind of GL-Lite platform, maybe?  Simplify, Simplify, Simplify.  This is just a tweak of my DNA drawing code, which is in turn based on "gears".   

Of course, another thing that I want to be able to do would involve L-systems, like this sort of thing from the article about the same on Wikipedia:

If I was a model railroading addict, I would of course want to be 3-d printing some of these. One of these days.  Maybe it's not as hard as it looks.

I asked Microsoft Co-pilot to write a C++ function that calculates the angle bisectors of an arbitrary triangle, without using branches or trig calls, and got this mess in response.  Can you see what is wrong here?  First of all, the response isn't in C++, but I am O.K., with that - I would just like an algorithm that works.  Second, there is some conditional logic, which I stated was not desired, i.e. if the dot product is non-negative do this, or else do that.  Lastly, the solution is of course completely wrong.  Care to see a solution that at least "appears to work", at least for now?  How about this one:

int triangle::generate_bisectors ()
{
    fpoint U1,U2,U3;
    MATH_TYPE d; 
    MATH_TYPE dx1,dx2,dx3,dy1,dy2,dy3;
    MATH_TYPE L1,L2,L3;
    MATH_TYPE c1,c2,c3,s1,s2,s3;
    // first find the sines and cosines
    // of the line segments that make up
    // the triangle
    dx1 = current[1].x-current[0].x;
    dx2 = current[1].x-current[2].x;
    dx3 = current[2].x-current[0].x;
    dy1 = current[1].y-current[0].y;
    dy2 = current[1].y-current[2].y;
    dy3 = current[2].y-current[0].y;

    L1 = sqrt((dx1*dx1)+(dy1*dy1));
    L2 = sqrt((dx2*dx2)+(dy2*dy2));
    L3 = sqrt((dx3*dx3)+(dy3*dy3));

    c1 = dx1*(1.0/L1);
    c2 = dx2*(1.0/L2);
    c3 = dx3*(1.0/L3);
    s1 = dy1*(1.0/L1);
    s2 = dy2*(1.0/L2);
    s3 = dy3*(1.0/L3);

    // now generate three points that
    // represent the directional unit
    // vectors for each line segment
    d = 1.0; // compass distance!
    U1.x = d*c1;
    U1.y = d*s1;
    U2.x = d*c2;
    U2.y = d*s2;
    U3.x = d*c3;
    U3.y = d*s3;

    // now generate the compass
    // points
    fpoint C1,C2,C3,C4,C5,C6;
    C1 = current[0]+U1;
    C4 = current[0]+U3;
    C2 = current[1]-U2;
    C5 = current[1]-U1;
    C3 = current[2]-U3;
    C6 = current[2]+U2;

    fpoint P0,P1,P2;
    // the directional unit vectors
    // can be used to find the midpint
    // of a line that besects an
    // isosceles triangle that forms
    // from the base of the "arrow"
    P0 = fpoint::midpoint (C1,C4);
    P1 = fpoint::midpoint (C2,C5);
    P2 = fpoint::midpoint (C3,C6);

    fline AP1,BP2,CP3;
    AP1 = fline (current[0],P0);
    BP2 = fline (current[1],P1);
    CP3 = fline (current[2],P2);

    J = fpoint::intersect (AP1,BC);
    K = fpoint::intersect (BP2,AC);
    L = fpoint::intersect (CP3,AB);

    return 0;
}

Here is the method in other words.  Using the Pythagorean identity, find the sines and cosines of each of the line segments.  Then generate a set of unit vectors that correspond to each line segment.  Add or subtract the unit vectors as appropriate to each vertex, to obtain a set of points equidistant from each vertex as if we were using a traditional compass.  Find the midpoint of each "little arrow" so generated.   Then generate a line segment that passes from each vertex through each compass midpoint, and then continue that line segment until it intersects the opposite side of the triangle.  Optimization is hopefully a job that can be carried out by any good modern compiler, yet I unrolled some operations like calculating the sine and cosine values for the normalized unit vector for each line segment.  Then I went ahead and used the implementations of some functions like midpoint and intersect in the point and fline classes which are defined elsewhere.  Finding the intersection of two lines, when they are defined in parametric form is pretty simple, by coding an implementation of Cramer's rule, like this:

fpoint fpoint::intersect (const fline &L1, const fline &L2)
{
  fpoint result;
  MATH_TYPE det,recip_det;
  det = L1.a*L2.b-L1.b*L2.a;
  if (det!=0)
  {
    recip_det = 1.0/det;
    result.x = (L1.b*L2.c-L1.c*L2.b)*recip_det;
    result.y = (L1.c*L2.a-L1.a*L2.c)*recip_det;
    result.m_bvalid = true;
  }
  else
  {
    result.m_bvalid = false;
  }
  return result;
}

Of course, this means that I broke my own rule against conditional expressions., but on any CPU that has branch prediction, the test should always succeed, that is if we are being given valid triangles, so the performance cost should be minimal if not zero in terms of execution time.  Or else, it could be #ifdef'd out in a more performance-based, and possibly in-lined version of the code.  Haven't tried it yet on the pipelined CORDIC solver that is built into the Parallax Propeller P2 chip, or else what writing my own tessellation and convex hull routines would look like, let's say CUDA style, that is to say, to bypass OpenGL for other, non-graphics related things, like vector fields in electricity and magnetism, fluid mechanics, etc.   Thus, the built-in methods are not always the best, the most desirable, or even useful, according to the situation.  Enjoy!

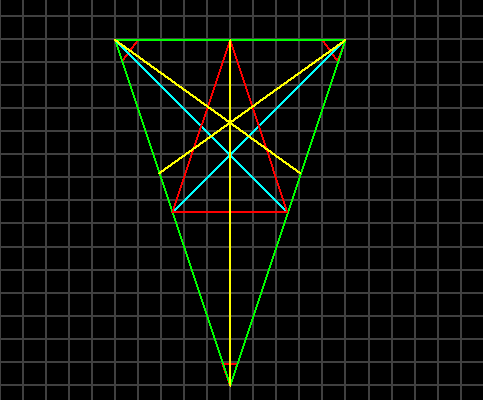
Consider the operations of a sequence of simple affine transformations being carried out on an ordinary equilateral triangle. It should be obvious, in that case, that the angle bisectors and the midpoint bisectors of each angle and side respectively, all intersect at the same point, a point which is commonly referred to as the centroid.  This property is invariant under simple shifting and rotation operations.  However, if the triangle is stretched along any axis, or pair of axes, to transform it into another triangle, such as one that is isosceles, then even though this can be accomplished through ordinary linear operations, the nature of the angle bisectors is such that the apparent symmetry is broken, even though they remain convergent amongst themselves.

Now as far as the midpoint bisectors are concerned, they still result in the creation of a set of points that also can be used to subdivide any arbitrary triangle into four similar triangles, each one-fourth of the size of the original – allowing for recursive tessellation, of course.  Yet if we introduce the angle bisectors into the process, and include them in our tessellation plan, this might provide a way to so also algorithmically generate a seemingly pseudo-random distribution of points, as it were, which might be useful for doing such things as defining the location of trees, blades of grass, hair follicles, or for defining other geometric forms.

The fact that Alan Turing himself was fascinated by the idea that oscillators regulated by chemical gradients might play a role in the determination of the distribution of stripes, or spots on such animals should not go un-noticed, either.  Even if this is all regulated by DNA of course, a cell still has to ask as if it were, not just “What am I”, or “Who am I”, but “Where am I?

Here is an interesting question:  What do you think about the idea of “intersectional mosaicism?”  Not so much as a social construct, but rather, from the point of view of epistemology. Yet this is something that I should clarify since I am more likely to be influenced by such modern as Chomsky, Penrose, or even Escher.  Yet another name comes to mind, and it is not Nietzsche. Sarte or Hagel, by the way.   I will get to that later.

Let’s get back to the idea of “intersectional mosaicism” therefore, based upon an epistemological framework rooted in the approach to physics known as “deep reductionism”.  Now some will theorize that everything is either male or female, or else is matter vs. energy, or it is math vs. geometry, or something like that.  I am not saying that those things aren’t relevant, rather I should say that the simple cherry-picking of taxonomies just because one can use PowerPoint or draw Venn diagrams is not the answer either.

Yet, if we embrace “intersectional mosaicism” as a social construct, a question might arise whether there is some formal operational scheme, like Maslow’s hierarchy of needs, or Ericson’s stages of maturation that must somehow describe everything.  Most of the time, such outlines are just as often as not, rooted in otherwise ad-hoc hypotheses at best, or else they are mostly pseudo-scientific constructions.

Whether to say, “to be or not to be”, or whether it is better to discuss the “is-ness of is”, or else “the being-ness of be” and what that means, let’s say, from the point of view of pure hedonism, is, another matter altogether.  Or is it?  In physics, spontaneous symmetry breaking, either is or is not, whatever Wikipedia says that is or is not, and that is all that I am going to say about that, for now. 

Yet what if from the point of view of pedagogy, something else altogether has been overlooked?  Something, that from the point of view of not only the mathematical framework of physics but so also from the point of view of the philosophical notion of the “construction of reality”, which might therefore have profound implications.

I started with some observations about triangles, which hopefully imply whatever that might imply.  Maybe this is a good time to mention Minsky, and Winograd, among others, as promised earlier, and then move on to the next topic – a perennial favorite:  wave matching in quantum systems, as well as applications, like turning audio into sheet music, and doing spectrum analysis using polyphase filter trees, when can then encapsulate multiple FFTs, each running with different bandwidths, sample rates, frequency ranges, sampling intervals, and so on.  With everything being re-split, re-overlapped, and of course re-combined, as if by magic, as it were, so that one model will dominate, insofar as providing a higher temporal resolution concerning note onsets, than is normally possible, that is according to the Rayleigh limit as it is normally perceived.  Then other methods of analysis provide enhanced frequency resolution, which is especially important at low frequencies.

An “intersectional mosaic” therefore, is not merely a “collage” as it were – as in some random art project, but something that has the potential to simultaneously blur traditional boundaries in regions of overlap, whether in a well-defined way or not.  Yet this should hint, therefore, as to the notion that so-called principles of “deep reductionism” might apply, so also in some social constructs even – if I dare to say it – and I just did.  For just as it should be obvious that the roots of logic are largely shared with geometry, and therefore algebraic topology.

Some will say that such ideas might invite some into the framework such things as theories about global economics, political upheavals, or those paths elsewhere that lead to the various wars, or opportunities for peace.  But that gets way ahead of things. In the meantime, LLMs I think are deficient in their implementation details, insofar as the quality of the framework is concerned, that is to say – to the foundations of their world model.  So maybe it is time to return to Euclid.  Or at least it is for me at least, at least that is for a while.

Turning audio into sheet music is one of my persistent passions. Experimenting with different polyphase filter tree topologies is always an adventure. 64? 128? 256? How many sub-bands? Sampling window size? That's another secret. Bessel, Butterworth or Gaussian window pre-processing, or a simple comb filter? That would be telling.

I've seen the comments in another forum that "if you are teaching magic, you are exposing magic!" And a LOT of people don't like that. But too bad! Maybe I should try decoding a certain famous Beatles chord. Not that it hasn't been done before. Yet in the meantime rtcp and llama integration is also a work in progress.  Actually, this is a VERY old project - just doing some updates, therefore.  Mainly what I am doing with this right now, then is fixing a lot of bugs, and doing a massive amount of project integration.  Wouldn't it be interesting to get LLAMA working on the one hand, and to try training it - or at least a version of Mega Hal on some MIDI data derived from real music? O.K. that is one thing, but another is just simply getting over a dozen or so projects, with names like DDE, Frame-Lisp, Rubidium, Debug-Terminal, Euclid, Construction, and so on - to "talk to each other" so to speak - with a much higher level of project integration that spans multiple projects than anything ever tried before.

Of course - who remembers this code snippet, from the original UCSD Pascal Compiler?

IDENTIFIER = RECORD
    NAME: ALPHA; LLINK, RLINK: CTP;
            IDTYPE: STP; NEXT: CTP;
            CASE KLASS: IDCLASS OF
              KONST: (VALUES: VALU);
           FORMALVARS,
               ACTUALVARS: (VLEV: LEVRANGE;
                   VADDR: ADDRRANGE;
              CASE BOOLEAN OF
                   TRUE: (PUBLIC: BOOLEAN));
                   FIELD: (FLDADDR: ADDRRANGE;
                      CASE FISPACKD: BOOLEAN OF
                        TRUE: (FLDRBIT,FLDWIDTH: BITRANGE));
             PROC,
             FUNC:  (CASE PFDECKIND: DECLKIND OF
                 SPECIAL:  (KEY: INTEGER);
                  STANDARD: (CSPNUM: INTEGER);
                  DECLARED: (PFLEV: LEVRANGE;
               PFNAME: PROCRANGE;
             PFSEG: SEGRANGE;
                CASE PFKIND: IDKIND OF
                 ACTUAL: (LOCALLC: ADDRRANGE;
                  FORWDECL: BOOLEAN;
                  EXTURNAL: BOOLEAN;
                  INSCOPE: BOOLEAN;
                  CASE BOOLEAN OF
                 TRUE: (IMPORTED:BOOLEAN))));
               MODULE: (SEGID: INTEGER)
END;

That is, of course how the compiler keeps track of identifiers, while compiling another program of course, or even if it is compiling itself.  Something is needed therefore, that goes beyond what people are doing with JSON, or other languages like RUBY or Python that allow creation of new data structures at run-time, which in principle is a form of "reflection".  That doesn't mean that our computers are actually self-aware, of course, but remember what I said earlier about Narcissus, who turned to stone after staring at his own reflection, or else there was also "Echo" who pined away for the love of Narcissus, that is, until only her voice remained.  All very cool.

So I was also checking out the download of the latest Ruby and Ruby on Rails distros, and it occurred to me that maybe I could add some Ruby integration as if maybe Ruby could just somehow be dropped into my framework - and then maybe, well things could get wild; because then I could pull in all of the Rails stuff, and maybe have "Ruby going off the rails - as it were."

And yet I still want to do something that works like SHRDLU, and then all of this needs to work with real physical robots.

Yeah, and in other news: I found my ancient IBM flowcharting template.

So while I have never been a big fan of flow charts, this might be a fun digression, given my latest obsession with DNA, hair, solar flares, and tessellations, with or without help from Euclid - of course.  Weird to contemplate that there are different pre-defined symbols for magnetic vs. paper tape input, or else manual input vs. punch cards, and so on.  A process seems to be a simple rectangle, whereas I/O operations are these other parallelograms.  Yeah, yeah, yeah.  And so it goes.

So, I found a copy of Euclid's Elements online and started reviewing some of the classic geometric methods., and then I got an interesting idea.  How hard would it be to implement all 200 or so proofs, or however many there are, in C++?  Of course, when working with computer graphics we have to proceed analytically, but that doesn't mean that we can't, at least in principle come up with ways to do some of the traditional compass and straight-edge constructions, that everyone seems to have forgotten with all of the 3-D mania.  Then again, there are some things quite wonderful and elegant about triangles, that are perhaps, underappreciated.  Like the fact we can subdivide a triangle by bisecting the edges, or else we can subdivide a triangle by bisecting the angles, and the results are not necessarily the same! Much to the surprise of many, no doubt! 

////////////////////////////////////////////////////////////////////
//
// PROP. IX.—Problem.
// To bisect a given rectilineal angle (BAC).
//
// THE ELEMENTS OF EUCLID - Translated by John Casey
// Published 1887 by Cambridge Press, public domain.
//
////////////////////////////////////////////////////////////////////

MATH_TYPE fpoint::law_of_cosines (const fpoint &p1,
const fpoint &p2, const fpoint &p3)
{
    MATH_TYPE A,bc,a2,b2,c2;
    MATH_TYPE dx1,dy1,dx2,dy2,dx3,dy3;
    MATH_TYPE result;
    dx1 = p2.x-p3.x;
    dy1 = p2.y-p3.y;
    a2 = (dx1dx1)+(dy1dy1);
    dx2 = p1.x-p2.x;
    dy2 = p1.y-p3.y;
    b2 = (dx2dx2)+(dy2dy2);
    dx3 = p1.x-p3.x;
    dy3 = p1.y-p3.y;
    c2 = (dx3dx3)+(dy3dy3);
    bc = sqrt(b2c2);
    result = (b2+c2-a2)/(2bc);
    return result;
}

 Well, here it is, therefore, in all of its glory - as we saw earlier, at least one method for subdividing triangles must be lurking somewhere, and by invoking such a process more or less recursively, we might want to consider how this can be extended to perhaps offer at least one way of generating the point cloud for a full head of hair, or a field of grass, or whatever else might come to the imagination.  Solar flares anyone?

What else might you be expecting? And then along came a spider, maybe?  That also seems doable!  There are so many different ways to build our model space, and not just with triangles or quads.  It might also be as if a web or a mesh might represent something else altogether, just like the fabric of space-time itself. This thought is so deep and so perfect, that when we contemplate the meaning of it - the perfect entanglement that is, in some other realm.

WARNING:  While the law of cosines method that I have described here seems to work most of the time, that is for most well-behaved triangles in the first quadrant, some triangles with obtuse angles. or other issues seem to give incorrect results, such as returning angle bisectors that are perpendicular to the correct angles.   In the meantime, have fun with this if you dare, since what I want to do with it is figure out a way to generate the bisectors, as well as do a bunch of other constructions, where feasible that is, without requiring any branches in the code!  And THAT is not at all as simple as it might seem when having to not only contemplate quadrant issues, obtuseness, rotations, etc.  Nonetheless, for purposes of CUDA style or OpenMP style parallelism, and/or pipelining, the more useful work that can be done without needing to have conditional logic, obviously should produce a substantial benefit when the problem at hand is put to scale, regardless of architecture.