The MLT-3 encoding has some interesting properties. In particular, it "works" in modulo 4: if the word to be sent has a number of 1s that is 0 mod 4 then we know that the output has gone through a multiple of a full cycle.
Similarly, if you take the parity of a given word, when it is even, then the output has done a full cycle or a half cycle. This has 2 combined effects :
- The parity bit is the least efficient error detection measure, but it is still good to have one.
- This parity can be chosen (even) to help reduce droop by forcing 1/4th turn on MLT3 for the next sub-word. The next bits will then be "dephased" by 0 or 1/2 turn.
Add to this the PEAC scrambler (with carry out), which ensures there is always at least one bit set (and one bit not set) and the parity becomes a way to force the "output phase" (state of MLT3) to either be
- inverted (+1 becomes -1 and vice versa)
- remain neutral (0 -> 0)
So it can be seen as a way to reduce wander. A bit. But it looks like a very interesting dual-purpose system that can both add protection (error detection) and increase signal integrity.
100Base-TX uses 4b/5b recoding to enhance integrity (by forcing transitions) with a 25% overhead, though unfortunately it gets wiped by the LFSR scrambler. In my early system, a 16-bit word gets 2 more bits (for check & framing), so it the overhead is 12.5% but if that at least 1 transition overall, it's spread over 18 bits... I'm ready to accept a bit more overhead to prevent baseline wander at the source.
There is already work (see the last log) to make the receiver droop-proof but it easily gets complex... My system does not have a specification for the maximum length or duration of a stable line level so I was preparing for the worst at first. But if I can significantly reduce this risk at the source, even at the cost of some bandwidth, I can simplify the receiver. It's even better if the extra bits serve as checks as well.
-o-0-O-0-o-
Now, how many bits are required ?
The (leading) pair of carry bits guarantee that at least one bit in the whole word is set. For 16 bits of data, total is 18 bits. The even parity bit provides "phase inversion", bringing the total to 19 bits.
If we want to ensure that the whole cycle is completed, we need 2 more bits : we get the "RTN" (Return To Neutral) convention that ensures that each word starts and ends with the neutral level at the start of the cycle. There could be 8 combinations:
- 000
- 001 010 100
- 011 110 101
- 111
The middle ones have more potential for reorganising the phases such that they are more balanced. But I have found three problems with this :
- This brings the total to 21 bits which is more than 25% of overhead
- 21 is a very inconvenient number, though it could be worse if it was prime. 21=3×7 so there is still some wiggle room but it's certainly not binary, not even even.
- It is not certain that returning to a given MLT-3 phase is desirable, because this could introduce some "bunching" in the power spectrum, at the packet level.
OTOH using 3 bits per packet could ease other parts of the circuit's design by processing the 18 bits in smaller subsets : 18=6×3 so there could be 3 identical groups of 6 bits to analyse, and local decisions can be individually taken.
The current choice is to set the total number of bits to 20, 16 data, 2 frame/carry, 2 parities. 20=2×2×5 which is far easier to process, serialise, deserialise and mentally process, and the overhead is again 25% just like 100Base-TX. So now we only have 2 extra bits to balance the wander. Let's make the best of it.
The consequence is that a full cycle can't be forced. However, it is necessary to keep the parity even, because the next word should start from 0 (one of the two zeroes). Otherwise it's impossible to know if the balance is good or bad, as a simple 90° shift can change the computations and we suppose it's not possible to know the state of the MLT3 FSM in advance.
For example, if a pattern 000000010100 starts from 0, it's fine because most of the 0 states will occur in the neutral state. But if it starts at +1, then there is a strong imbalance towards +1 which should be broken up.
Hence : we shouldn't create the full-turn-per-word rule to prevent certain harmonics but we need to keep the 0-or-180° constraint to keep the balancing computations simple enough. It's less damaging to the spectrum but it simplifies the decisions for the padding. So it's another encoding constraint : Return To Neutral (or Zero) at the word level, which is enforced with parity, but there are 2 parity bits now.
As a rule of thumb, both P bits should be 1 unless the data's parity is odd, then the only thing to choose is which bit to clear, which is another story...
-o-0-O-0-o-
This raises yet another question: where do these extra bits go ?
Ideally in the middle of the word, so it can "flip" neighbouring parts and prevent long sequences of identical levels.
Given 20 bits, including 2 parities, we get 18 bits of data which is 6×3:
- 2 bits for frame/crc
- 4 data
- 1 parity
- 6 data
- 1 parity
- 6 data
And here you have your frame.
Parity/balancing takes place after the scrambler, in a new pipeline stage.
Parity / popcount is calculated individually on each of the three 6-bit groups, giving three 3-bit numbers that are then compared to elect which parity bit (if any) should be disabled.
Popcounts higher than 3 (4,5,6) wouldn't need to be bothered with because they provide enough swings to rebalance the average, overall. The algorithm should focus on popcounts less than 3 which have a risk of greater imbalance and longer runs of +1s or -1s. But then, it also depends on the phase because the 00000 could occur during a neutral phase. So the popcounts should only count the +1 and -1, not the number of transitions: the input should be filtered by XORs...
playing around with XOR gates...
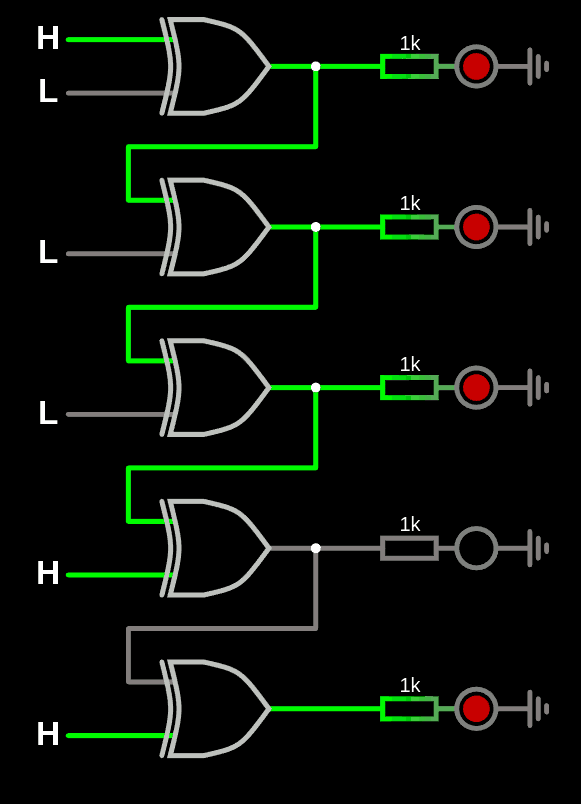
Or maybe a LUT would be more practical and configurable.
.....
... something something... maybe for the next log.
....
Having only 2 parity bits limits the inter-word wander rebalancing. But each word can be processed in parallel.
The other effect is that there is now a guarantee that each 20-bit word has at least 2 changes. So this means a loss of data (absence of packet) can be detected in less than 20 bauds, and a +1 or -1 state can't last longer than 6 bauds.
.
There is more to come and dig but it looks quite promising. And reducing the number of parities to 2 is also good because it also limits the conditions to consider for flipping either of them.
 Yann Guidon / YGDES
Yann Guidon / YGDES
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.