So we have a unit that takes 18 bits and outputs 18 bits, whose values are as dependent from the others as permitted by only 64 XOR gates. Let's call it the H unit, because it tries to maximise the Hamming distance of the input word.

This has been designed already, and I picked the encoder of a previous log:

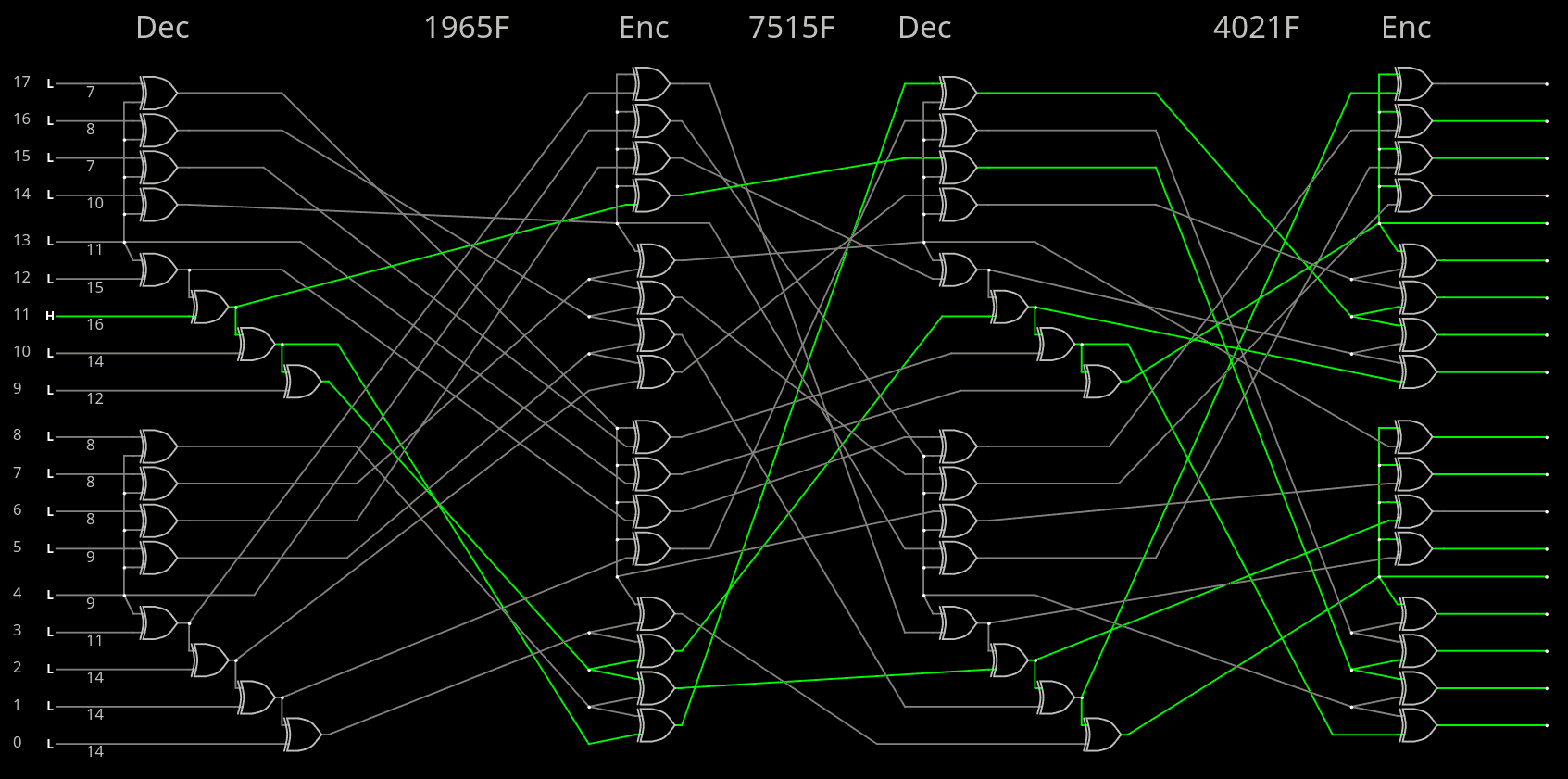
As noted before, it has some of the best possible avalanches I could find: 7 7 8 8 8 8 8 9 9 10 11 11 12 14 14 14 14 15 16 is not perfect but as good as it can be, within the constraints of parsimony of the project.

We also know some of its flaws, by reading the avalanches of the reverse transform : a few combinations need only a few bits to flip only one bit, as indicated by the start of the avalanche sequence : 2 2 3 4 4...

So, since the unit would be looped on itself, another permutation is required to amplify this even more, making sure these few weak bits are fed back to the strongest ones.

But first, let's untangle this mess because there are a looot of crossings that would make P&R uselessly harder.

...........

The untangled circuit has had a weird episode.

The score has changed ! 7 8 8 8 8 9 9 9 9 11 12 13 14 15 15 15 15 15

The 16-bit avalanche has disappeared, as well as one of the 7-bits.
However now we have five 15 and the sum of avalanches has climbed to 200 (vs 188 for the original version, max score is 18*18=324). I don't know how or why but that's good !

Version with even fewer crossings :

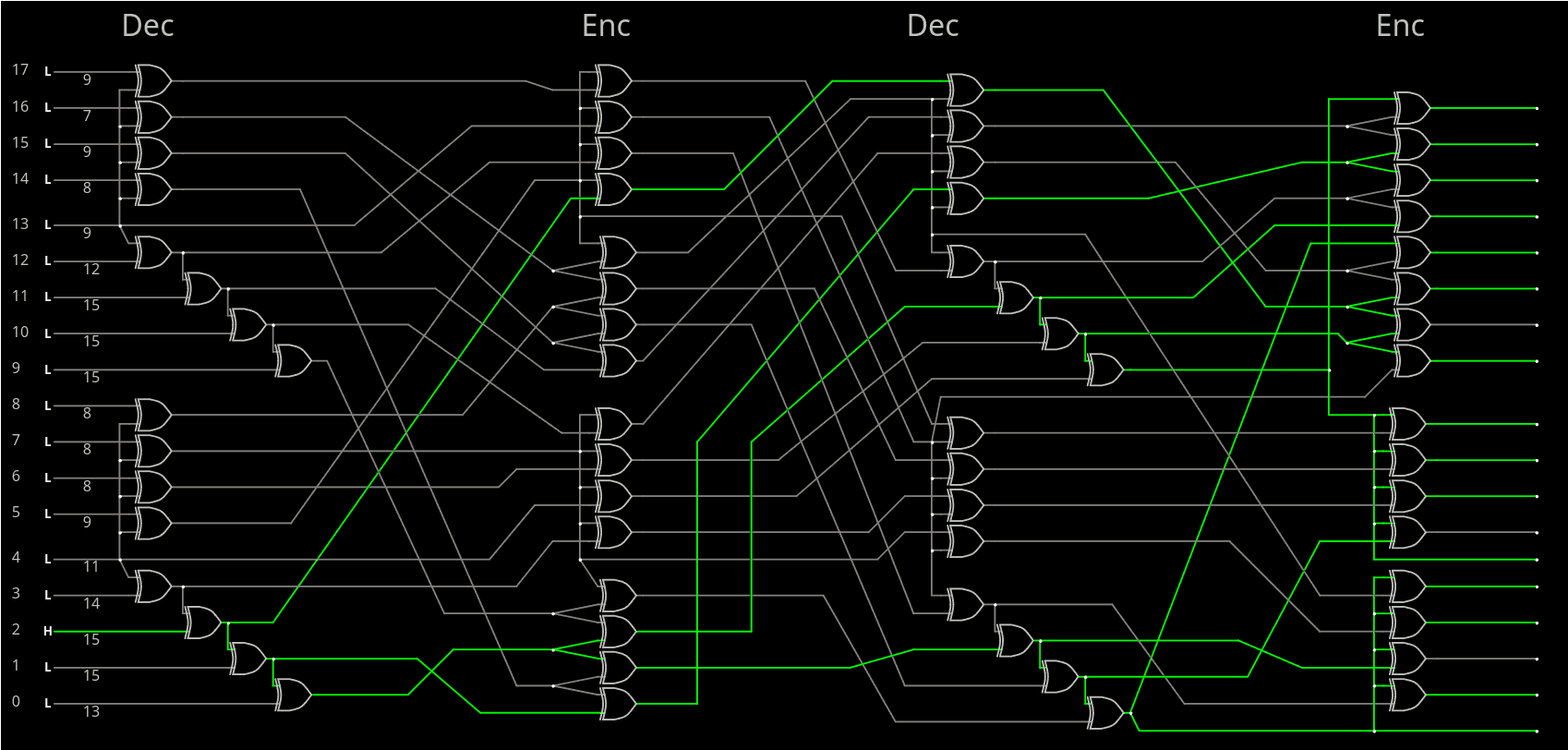
I checked : same behaviours, despite changing the place of the end gates.

....

And now, the VHDL, and...

 0 : 13   110111011111011001
 1 : 14   110111011111011011
 2 : 14   110111101111011011
 3 : 13   110111101110011011
 4 : 10   010111100100110101
 5 :  8   110001101001001010
 6 :  8   000000011111111000
 7 :  9   101110111001000100
 8 :  8   111111000010100000
 9 : 15   111111011111111001
10 : 16   111110111111111101
11 : 14   111110111111110001
12 : 11   001101111111010001
13 :  9   000111100010110101
14 :  7   110111000000100010
15 :  9   111111000000101100
16 :  8   100001001111110000
17 :  9   000000011111111010
  total:195

What the !!!!

7 8 8 8 8 9 9 9 9 10 11 13 13 14 14 14 15 16

5 fewer in total and 16 has appeared again, yet still only one 7,

I give up.

.

After all the minimum requirements are met and too much optimisation toward high numbers make combinations behaving inappropriately.