In our last post, we discussed how to select the right detector length and focusing lens. Now, we're going to dive into the optics of the grating itself, specifically how it affects magnification in your system.

https://hackaday.io/project/202421-jasper-vis-nir-spectrometer/log/243375-part-5-a-guide-to-selecting-detector-length-and-focusing-lens-for-grating-spectrometer

The Anamorphic Nature of a Grating Spectrometer

A grating spectrometer is an anamorphic optical system, which means it magnifies in different ways along different axes. To briefly review this property, assume the entrance aperture of the spectrograph is a slit of width W and length L, aligned so that its projected image lies perpendicular to the direction of dispersion. The projected length l at the detector is then:

where F_F; and F_C; are the focal lengths of the imaging lens and collimating lens, respectively.

However, there's another crucial magnification at play—the magnification in the direction of the dispersion. This is a direct result of how light interacts with the grating.

Deriving the Magnification from the Grating

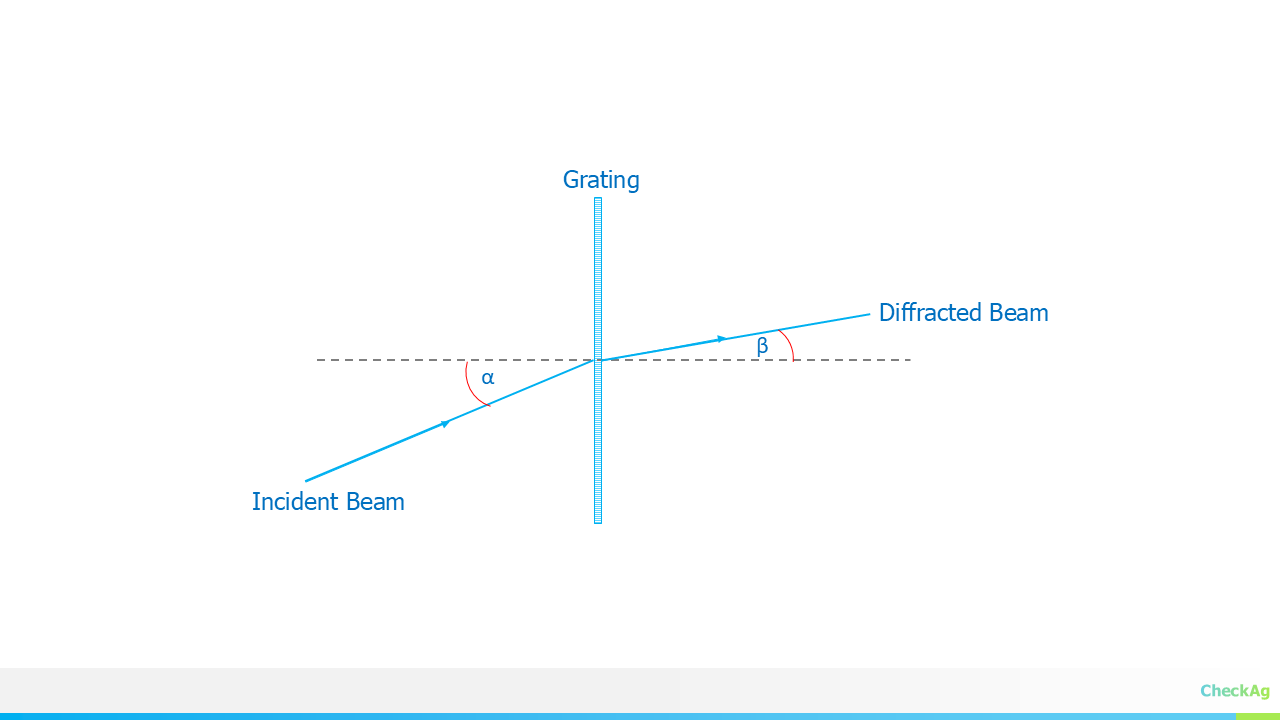
To understand, let's consider the grating equation, which describes the relationship between the angles of the incident and diffracted light.

where:

• m is the diffraction order
• λ is the wavelength of light
• d is the groove spacing of the grating
• α is the angle of the incident ray with respect to the grating normal
• β is the angle of the diffracted ray with respect to the grating normal

Now, let’s consider two rays originating from opposite edges of the entrance slit. These two rays arrive at the grating with incident angles that differ by a small amount, Δα. After passing through the grating, the diffracted rays will leave with an angle difference of Δβ, where Δβ ≠ Δα. 

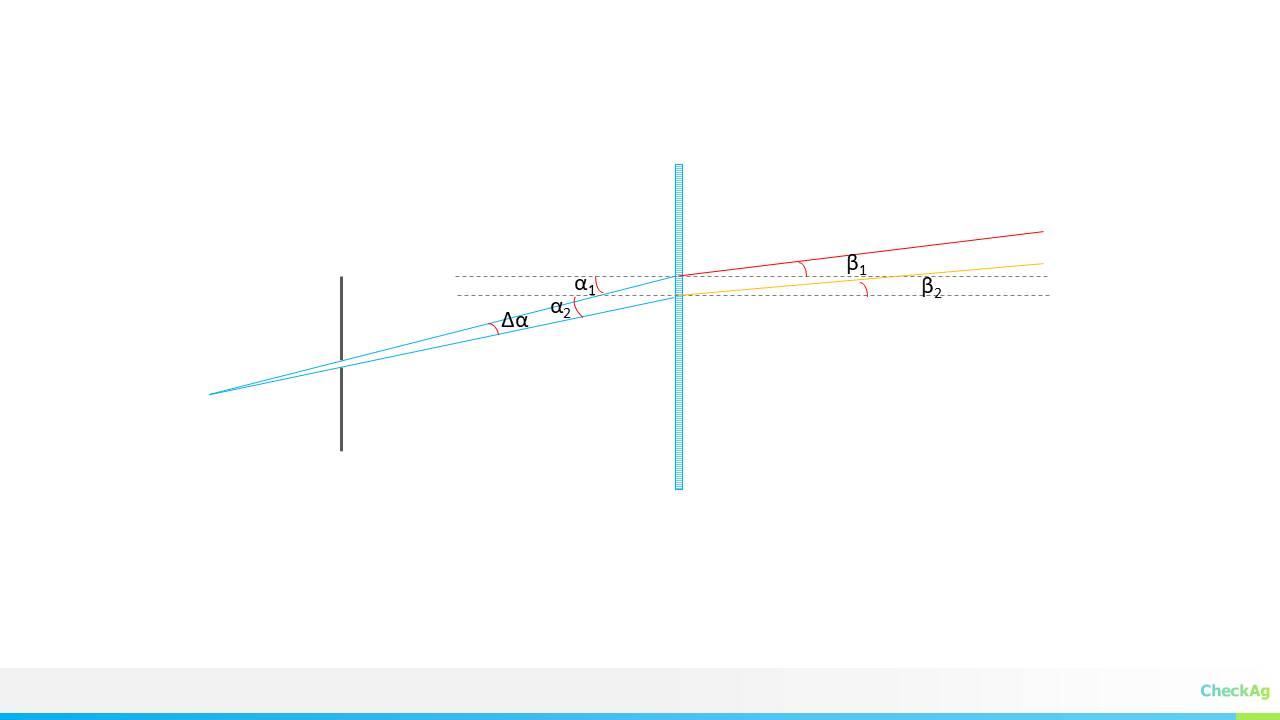
The magnification of the grating, r, is defined as the ratio of these two angular changes:

To find the relationship between Δβ and Δα, we can differentiate the grating equation with respect to α and β, while assuming the wavelength (λ) is constant.

Let's start with the grating equation:

Since m, λ, and d are constants for a single wavelength, their product is also a constant. Therefore, the derivative of the left side of the equation is zero. We can differentiate the right side with respect to α and β:

Using the chain rule, this becomes:

Rearranging the terms to solve for the ratio of dβ to dα, we get:

The magnification, r, is the ratio of the change in the diffracted angle to the change in the incident angle. In the limit of very small changes (Δα and Δβ), we can replace dβ/dα with Δβ/Δα. Since magnification is typically concerned with the magnitude of the angular change, we take the absolute value:

This term, cosα / sinβ, is the anamorphic magnification factor of the grating itself

Putting It All Together: The Total Magnification

The overall magnification (M) of the spectrometer is the product of the magnification from the lenses and the magnification from the grating. Therefore, the total magnification is:

From this, you can solve for the focal length of the collimating lens F_c :

In practical spectrometer design, a magnification (M) close to 1 is often targeted to maintain a one-to-one relationship between the slit and the detector image.

In the next post, we'll discuss the final component of our optical system: the entrance slit, and how its width impacts the spectral resolution of your spectrometer.