So how can we detect 3rd intermediate value using only standard CMOS integrated circuits? There is one trick - if we take 2-input NOR gate and 2-input NAND gate with connected inputs then they will NOT work as regular CMOS inverters! They will have "shifted" thresholds (important detail - it has to be "unbuffered" CMOS ICs as CD4001UBE and CD4011UBE):
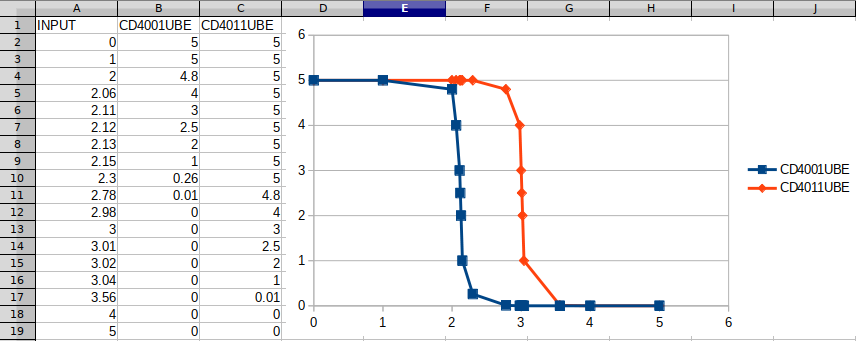
Those measurements were taken from actual CD4001UBE and CD4011UBE chips connected to +5V:

So we have this truth table (let's call intermediate value O):
| Input | NOR gate (CD4001UBE) | NAND gate (CD4011UBE) |
| 0V (N) | P | P |
| +2.5V (O) | N | P |
| +5V (P) | N | N |
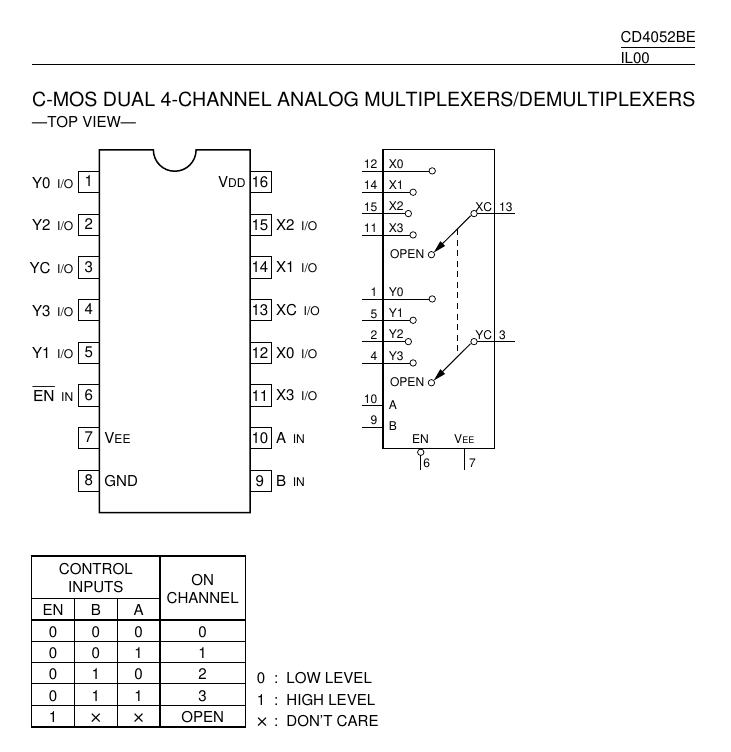
After that we may use CMOS 4:1 selector CD4052BE to choose from 3 pre-defined ternary values (1 value will never appear so we can simply repeat intermediate value twice to get all 4) to implement some specific ternary functions (like NOOP will implement ternary inverter and POON will implement ternary buffer):
Using only these 3 kinds of CMOS ICs we may build more complex ternary circuits including actual ternary computer :)
https://www.digikey.com/en/products/detail/texas-instruments/CD4001UBE/525852
https://www.digikey.com/en/products/detail/texas-instruments/CD4011UBE/525867
https://www.digikey.com/en/products/detail/texas-instruments/CD4052BE/67307
And it should be multiple times cheaper than building ternary computer on expensive switches DG403 :)
BTW this approach could be directly translated to actual IC manufacturing with standard CMOS tech process...
 SHAOS
SHAOS
 john.ohno
john.ohno

 will.stevens
will.stevens
Fun!
It's tricky to do this discrete, because you don't know the input threshold voltage of just any chip (or, you have to characterize each one you use..). Fortunately, the average chip tends to be, well, pretty average, so although there's no guarantees here, the observed results are fairly likely.
Quite right about monolithics: maybe with some extra gate threshold control (to obtain reliable input thresholds, say 30/70% low-mid/mid-high), a reasonable noise margin could be had, while transistor matching permits large scale integration.
Practical downsides: 1. How does one generate a true ternary output level that's well-defined? 2. How to implement a ternary truth table (what even makes a good "common" ternary function, anyway?), other than translating to binary and solving it with many more (boolean) gates?
What's interesting about using ganged inputs like this: it hints at another style of logic gate, amenable to discrete/analog implementation. Consider an N-input gate, which performs a comparison to the unary input sum. That is, an "at least M out of N inputs hot" function. If we set threshold > 0, this is simply an OR gate; for threshold >= N, AND. But instead of these strict cases (all-off, all-on), we have intermediate cases too. There aren't many applications, I think, for these; but it would be another tool in the kit for reducing k-maps. It's easily implemented with RTL style gates -- anywhere a bunch of inputs are divided with resistors and summed to an input terminal (gate/base/grid). It's easy to see how this arises in the CMOS case, too -- and why unbuffered gates are required :)