I got a bit stuck with the work I was planning for today, so I wrote something else to regain motivation: a fractal! Rendering takes a while (8242 seconds), being fully interpreted and lacking multiplication, and even without the "right-shift" operation you badly need for this. All those must be mimicked with slow high-level code using just addition and subtraction. [Edit: it takes 1127 seconds now with native code for "right-shift"]

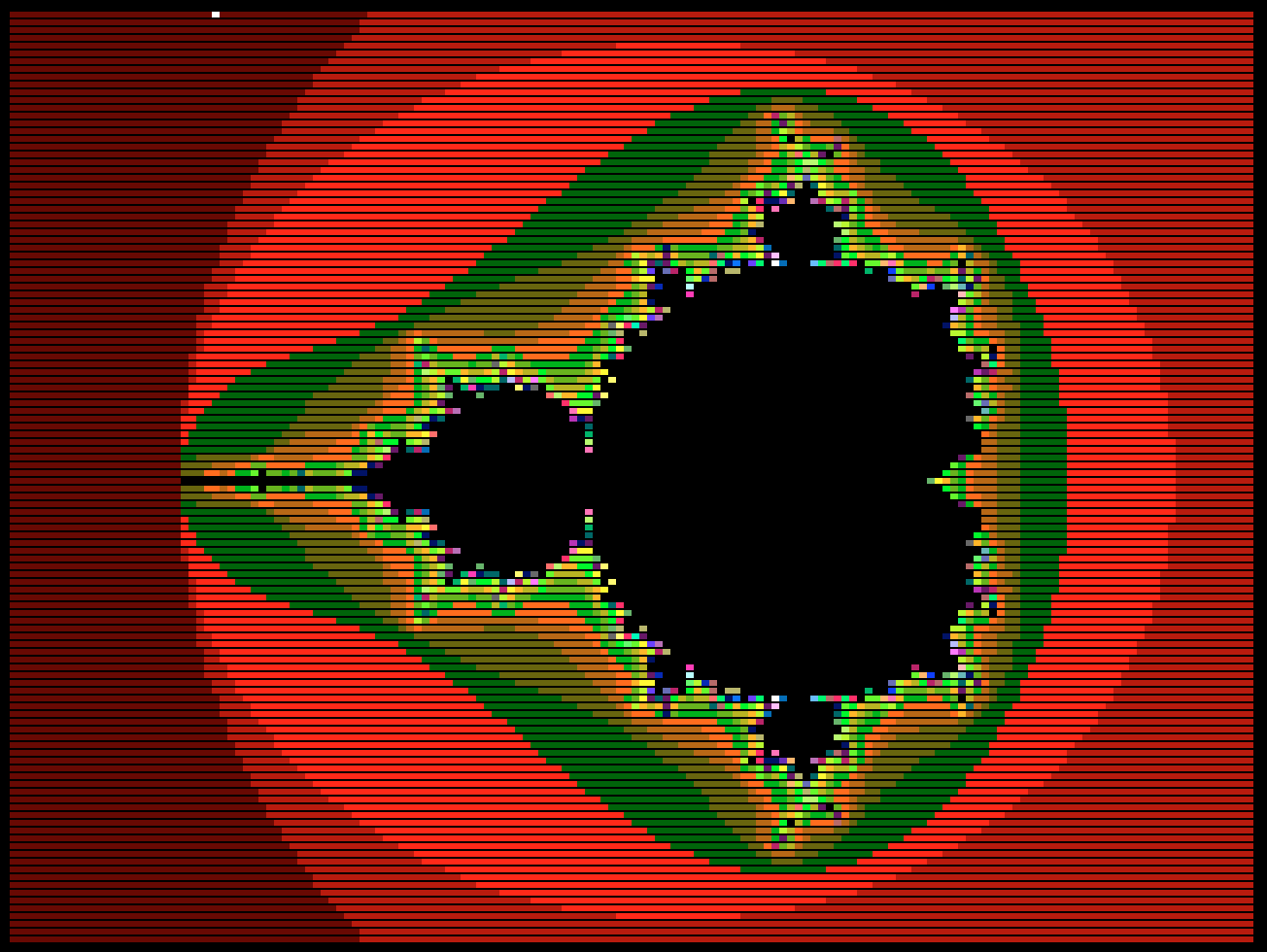
It should be easy to speed the whole thing up a lot just by adding a right-shift assembly function. Next time... GCL source code:

{-----------------------------------------------------------------------+
|                                                                       |
|       Mandelbrot fractal                                              |
|                                                                       |
+-----------------------------------------------------------------------}

gcl0x

{
  Plot the Mandelbrot set

  - 160x120 pixels and 64 colors
  - Faithful translation of mandelbrot.c pre-study
  - Use 16-bit vCPU math as 7-bit fixed point arithmetic (1.00 -> 128)
  - Implement multiplication in interpreter
  - Implement shift-right in interpreter as well
  - A bit slow (8242.655 seconds)

  XXX At the end change all to grey tones and redo
  XXX Redo at different sections
  XXX Tone for every pixel value
}

{-----------------------------------------------------------------------+
|                       RAM page 3                                      |
+-----------------------------------------------------------------------}
$0300:

{ Pretty accurate multiply-shift ((A*B)>>7), but it can be off by one }
[def
  push

  {Extract sign and absolute values}
  0 sign= C=
 {0}A- [if>0 A= 1 sign=]
  0 B- [if>0 B= sign 1^ sign=]

  {Multiply}
  7 shift= {Pending shift}
  $200
  [do
    bit=
    -$4000 C+ [if<0
      C C+ C=
    else
      {Shift prematurely in an attempt to avoid overflow}
      B ShiftRight! B=
      shift 1- shift=]

    {Add partial product}
    A bit- [if>=0
      A=
      C B+ C=]

    bit ShiftRight! if<>0loop]

  {Shift}
  [do
    C ShiftRight! C=
    shift 1- shift= if>0loop]

  {Apply sign to return value}
  sign [if<>0 0 C- else C]

  pop ret
] MulShift7=

{ Calculate color for (X0,Y0) }
[def
  push
  0 X= XX= Y= YY= i=
  [do
    i 1+ i= 64^ if<>0           {Break after 64 iterations}

                                {Mandelbrot function: z' := z^2 + c}
    X A= Y Y+ B= MulShift7! Y0+ Y= {Y = 2*X*Y + Y0}
    XX YY- X0+                  X= {X = X^2 - Y^2 + X0}

                                {Calculate squares}
   {X}A= B= MulShift7!          XX=
    Y A= B= MulShift7!          YY=

    -$200 XX+ YY+ if<0loop]     {Also break when X^2 + Y^2 >= 4}
  i
  pop ret
] CalcPixel=

{-----------------------------------------------------------------------+
|}\vLR>++ ret{          RAM page 4                                      |
+-----------------------------------------------------------------------}
$0400:

[def
  push

  $7ff p= {Start of video (minus 1 to compensate for 1st step)}

  -323 X0= 3 DX= 161 Width=  {Horizontal parameters}
  -180 Y0= 0 DY= 120 Height= {Vertical parameters}

  [do
    {Length of next segment, either horizontal or vertical}
    DX [if<>0 Width 1- Width= else Height 1- Height=] if>0
    [do
      len=

      {Step in the fractal plane}
      X0 DX+ X0=
      Y0 DY+ Y0=

      {Matching step in video frame}
      DX [if<0 p 1-     p=]
      DX [if>0 p 1+     p=]
      DY [if<0 -$100 p+ p=]
      DY [if>0  $100 p+ p=]

      63 p. {White while busy here}

      {First check if we are inside one of the main bulbs for
       a quick bailout (Wikipedia)
       (x+1)^ + y^2 < 1/16}
      Y0 A= B= MulShift7! YY=
      X0 128+ A= B= MulShift7! YY+ 8- [if<0 0
      else

      {q*(q + x - 1/4) < 1/4*y^2, where q = (x - 1/4)^2 + y^2}
      X0 32- A= B= MulShift7! YY+ {q}
      A= X0+ 32- B= MulShift7! tmp=
      tmp+ tmp= tmp+ tmp= {*4} YY- [if<0 0
      else

      {Otherwise run the escape algorithm}
      CalcPixel!
      ]]
      p. {Plot pixel}
      len 1- if>0loop]

    DY tmp= DX DY= 0 tmp- DX= {Turn right}
    loop]
  pop ret
] CalcSet=

{-----------------------------------------------------------------------+
|}\vLR>++ ret{          RAM page 5                                      |
+-----------------------------------------------------------------------}
$0500:

{ Stupid shift-right function }
{ XXX Better make a SYS extension for this }
[def
  a= 0 b=
  $8000 a+ [if>=0 a= $4000 b+ b=]
  $c000 a+ [if>=0 a= $2000 b+ b=]
  $e000 a+ [if>=0 a= $1000 b+ b=]
  $f000 a+ [if>=0 a= $0800 b+ b=]
  $f800 a+ [if>=0 a= $0400 b+ b=]
  $fc00 a+ [if>=0 a= $0200 b+ b=]
  $fe00 a+ [if>=0 a= $0100 b+ b=]
  $ff00 a+ [if>=0 a= $0080 b+ b=]
  $ff80 a+ [if>=0 a= $0040 b+ b=]
  $ffc0 a+ [if>=0 a= $0020 b+ b=]
  $ffe0 a+ [if>=0 a= $0010 b+ b=]
  $fff0 a+ [if>=0 a= $0008 b+ b=]
  $fff8 a+ [if>=0 a= $0004 b+ b=]
  $fffc a+ [if>=0 a= $0002 b+ b=]
      a 2& [if<>0          b<++ ]
  b ret
] ShiftRight=

{-----------------------------------------------------------------------+
|}\vLR>++ ret{          RAM page 6                                      |
+-----------------------------------------------------------------------}
$0600:

{ Main }
[do
  CalcSet!
  60 \soundTimer. {For debugging}
  loop]

{-----------------------------------------------------------------------+
|       End                                                             |
+-----------------------------------------------------------------------}