If we try to summarize what we have seen so far:

1. Arithmetic operations on arbitrary analog values are better performed using digital numbers to get a repeatable accuracy
2. Unsigned integer digital numbers are represented as base 2 (binary) numbers using only 0 and 1 values, using a positional notation with enough binary digits (bits). Using only 2 values offers the simplest and most effective design to store digital numbers in a physical device
3. Signed integer digital numbers are represented using a 2's complement notation but otherwise follow the same arithmetic rules as unsigned integer digital numbers
4. Non-integer numbers can be represented using:
   1. a fixed-point notation where the decimal point position is implicit and a given number of bits right of it are used to hold the fractional part of the number, following the same arithmetic rules as integer digital numbers
   2. a floating point notation where the decimal point position is given by an integer exponent, and the remaining bits hold the fractional part of the number as the mantissa. Both the exponent and mantissa parts still follow the same arithmetic rules as integer digital numbers
5. Arithmetic operations on digital numbers can be reduced to subtraction operations
6. Subtraction operation can be implemented using the basic logic operations from the Boolean algebra, although adding the addition operation does not cost much, and having positional shift or rotation operations helps implementing multiplication and division operations more efficiently, which would otherwise require complex specific hardware
7. Simple as well as bitwise (i.e., performed on a set of bits that can be used equivalently to store a digital number) logic conditions  can of course be implemented using the same basic logic operations from the Boolean algebra

Thus, digital computers can perform all arithmetic and logic operations only using Boolean algebra values, operations and laws, which will be described below in details, using simple undergraduate maths.

It is thus a formalism for describing logical relations in the same way that ordinary algebra describes numeric relations.

Values

Unlike elementary algebra which deals with an infinite set of numbers, Boolean algebra is using a finite set of only 2 elements. These 2 values can be indifferently called true and false, T and F, 0 and 1, or any other couple of symbols, but they are generally represented with the bits (binary digits) 0 and 1, as the XOR (exclusive-or) and AND (conjunction) operations (see below) plays the role of the addition (+) and multiplication (x) operations in integer arithmetic modulo 2, for which 1 + 1 = 0, but unlike common arithmetic, where 1 + 1 = 2. The OR operation (inclusive-or or disjunction) is then defined as x + y + xy.

Manipulating only 2 values is very nice, since it enables using the method of proof of perfect induction or proof by exhaustion, i.e., the verification for all possible cases for demonstrating theorems, as the number of cases is very small.

Operations

Boolean operations are functions having zero or more Boolean input values (in the set {0, 1}) to a single Boolean output value.

The number of operands is the arity of the operation. An operation of arity zero, or 0-ary operation is a constant, and the Boolean algebra only deals with unary operations (with arity 1) and binary operations (with arity 2).

Unary Operations

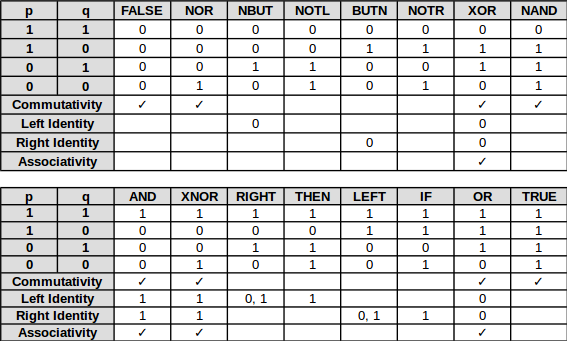
If we consider all possible calculations from 1 binary input value p to an output value, there are only 2 ^ 2 = 4 unary operations:

Binary Operations

For calculations from 2 binary inputs p and q to an output values, each inputs with two possible values, there are 2 ^ 2 = 4 possible combinations of inputs. Because each output can have two possible values, there are 2 ^ 4 = 16 possible binary operations:

• Commutativity means that the operation follows the identity p OP q = q OP p holds, i.e., for p ≠ q (for the lines in the table above where p = 0 and q = 1 or p = 1 and q = 0), the result is the same.
• Left identity, when present, provides the value(s) p on the left side of the operator that leaves the value on the right side of the operator unchanged.
• Right identity is the same on the other side of the operator with value(s) of q.
• Associativity means that for 3 binary values a, b and c, the identity (a OP b) OP c = a OP (b OP c) holds. This is equivalent to say that the operator has both left and right identity and it is the same value.

Here are enumerated all possible operations, and their equivalent representations:

Basis

The operations need not be all explicitly stated. A basis is any set from which the remaining operations can be obtained by composition. A Boolean algebra may be defined from any of several different bases. There are three bases for Boolean algebra that are in common use:

• The lattice basis containing the [AND, OR, NOT] operations mostly used for logical processes. Most treatments of Boolean algebra assume the lattice basis
• The ring basis containing the [AND, XOR] operations mostly used for abstract algebra considerations
• Since all operations can be defined in terms of the Sheffer stroke [NAND] (or its dual [NOR]) operations, the resulting single-operation basis has become the basis of choice for analyzing digital circuits, as all circuits can be turned into a combination of NAND (or NOR) operations

Laws

If we assume the lattice basis, the Boolean algebra satisfies a set of identities between two Boolean terms, where a Boolean term is defined as an expression built up from variables, the underlying set of constants 0 and 1 and using the 3 basic operations ( [AND, OR, NOT]) . These identities are called laws, which can conveniently be proven using the method of proof of perfect induction, given the small number of cases.

Monotone Axioms

If we use the symbols commonly used for analyzing digital circuits (‧ or implicit for AND, + for OR and ~ for NOT), the following axioms hold:

All of the laws above use only AND and OR operations. These operations have the property that changing either argument either leaves the output unchanged or the output changes in the same way as the input. Equivalently, changing any variable from 0 to 1 never results in the output changing from 1 to 0. Operations with this property are said to be monotone.

Nonmonotone Axioms

Nonmonotonicity enters via complement operation NOT as follows:

The above axioms (Ia) to (Va) and their dual (Ib) to (Vb) are the ones introduced by Edward V. Huntington in his paper "Sets of Independent Postulates for the Algebra of Logic" pp 293-293 in 1904 as postulates bearing the same reference numbers in its first set of postulates (his postulates Ia, Ib and VI are provided by the lattice basis and the fact that the set of Boolean values contains 2 distinct elements, {0, 1}).

These axioms are sufficient to prove all the other laws below:

Monotone Laws

More monotonous laws were introduced by Huntington:

Nonmonotone Laws

And one more nonmonotonous law was also described in Huntington's paper (lawn XIV is not):

De Morgan's Laws

However, whereas ordinary algebra satisfies the 2 laws:

(-x)+(-y) = -(x + y)
(-x)(-y) = xy

Boolean algebra satisfies De Morgan's laws:

These are the 2 last laws from Huntington's paper, and not surprisingly, form an indispensable tool when simplifying digital circuits involving AND, OR and NOT operations ("gates").

Other Nonmonotone Laws

Some other laws can be proven (make sure to display the "Proven properties" panel):

The first motivation that predated the early computers was to automate arithmetic calculation algorithms, so it is no wonder if an arithmetic unit is at the heart of the processor and the computer itself.

But besides calculation, algorithms can also perform data processing (including validation, sorting, summarization, aggregation, analysis, reporting, classification, etc.) and automated reasoning, which both require formal mathematical logic instead of ambiguous rhetoric, syllogism or philosophy in order to be fully automated.

This is why the arithmetic unit is always completed with a logic unit to form the Arithmetic and Logic Unit (ALU) as the central part of the processor and computer.

Arithmetic

Formally, arithmetic is the branch of mathematics that studies numbers, and especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. But of course, this greatly depends on how the number are represented. Even if today the main numeral system is the Hindu–Arabic one, this has not always been the case.

There have been numeral systems using 2, 3, 4, 5, 6, 8, 10, 12, 16, 20 or 60 as a base. BTW, duodecimal (base 12) is still used today for counting hours and in music, whereas sexagesimal (base 60) is also used for measuring time, angles and geographic coordinates, mainly because of their superior highly composite number property, that makes them a more convenient number system for computing fractions than most other number systems.

But only considering the common decimal (base 10) numeral system, the positional notation where each symbol represents an order of magnitude ("ones place", "tens place", "hundreds place", etc.) was only introduced in Europe by Leonardo Fibonacci in 1202 in his Liber Abaci, but is in wide use only since much later (since the middle of the 16th century), replacing the Roman numeral system (which is still used today in certain contexts such as years) because of its easier arithmetic rules.

If handling digits having 10 possible symbols or values is still possible using mechanical devices with wheels, gears and teeth or cogs, this approach is difficult to transpose to electro-mechanical relays (their contact can only be in 2 different states: open or closed) or fully electronic vacuum tubes or solid-state transistors. Even if vacuum tubes and transistors can be used in analog circuits to represent an infinity of continuous values, we already saw in Part 1 that digital computing was a much better solution.

The idea of using 2 bands of analog values as far apart as possible from one another to provide the best immunity against glitches leads to consider using a binary (base 2) numeral system with positional notation, as devised by Gottfried Wilhelm Leibniz in "Explication de l’arithmétique binaire, qui se sert des seuls caractères O et I avec des remarques sur son utilité et sur ce qu’elle donne le sens des anciennes figures chinoises de Fohy" in 1703 (translation into English here).

Except for a few esoteric machines, all computers today are using binary numbers extensively, although not all arithmetic operations are supported in hardware, as the most complex ones (multiplication, division and square root) can be carried out by a software algorithm using additions/subtractions and left/right number positional shifts.

The positional left shift on a binary number is equivalent to adding a number to itself, whereas the positional right shift on a binary number can (expensively) be obtained by repeatedly incrementing a counter once while another counter is incremented twice and matched against the binary number to shift positionally right. Thus, left/right number positional shifts can be obtained from additions only and are not strictly required to perform all arithmetic operations.

And because of the general rules of arithmetic, all operations on numbers can be decomposed into a series of operations on 2 numbers called operands, producing a single result.

Moreover, as the method of complements which was used in many mechanical calculators as an alternative to running the gears backwards can be transposed to other digital techniques to perform subtraction, implementing an arithmetic unit can thus be limited to having a 2-operand binary number subtractor only, as x+y can be computed as -(-x-y)!

Logic

Whereas arithmetic deals with specified numbers, algebra introduces quantities without fixed values, known as variables.

Formally, the Boolean algebra is a branch of algebra in which the values of variables are the truth values true and false, as formalized by George Boole in his two famous books "The Mathematical Analysis of Logic" (1847) and "An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities" (1854).. It is a symbolic method of investigating logical relationships (or propositions) where no limitation has been placed on the number of elements. From Edward Huntington’s postulates (fourth set, given on page 280) published in 1933, it can be demonstrated that in every Boolean algebra there are two specific elements: the identity elements. Hence, any Boolean algebra has at least two elements.

In his 1937 paper "A Symbolic Analysis of Relay and Switching Circuits", Claude Shannon implemented a two-element Boolean algebra with a circuit of switches, where a switch is defined a device that can be placed in either one of two stable positions: off or on. These positions can just as well be designated 0 and 1 (or the reverse). For this reason, the two-element Boolean algebra has been called switching algebra. Basically, his paper demonstrates that this two-valued switching algebra is isomorphic with propositional logic as defined by George Boole. Hence, whatever terminology, operations, and techniques are used in logic can be applied to Boolean algebra, and vice versa, to the point that today switching algebra and Boolean algebra are often used interchangeably.

It is thus perfectly valid to use a binary digit to represent a logic condition, and use the Boolean algebra to perform logic operations that are part of algorithms.

Bitwise Operations

As just demonstrated above, a single binary digit or bit can be used to represent a logic condition, and multiple bits can be used to represent a binary number. But multiple bits can also be considered as a collection of single bits at the level of their individual bits, on which the Boolean (or switching) algebra applies too. Such Boolean operations on collections of bits (NOT, AND, OR, XOR) are called bitwise operations, and these are often completed by other operations on these sets of bits in the form of positional shifts or rotations, which we found previously useful for some arithmetic operations.

Switching algebra was introduced in terms of two binary operations (AND and OR) and one unary operation (NOT). Every switching expression is solely made up of variables connected by various combinations of these three operators, which leads to the concept of functionally complete or universal set of Boolean operations. It follows that the set of operations {AND, OR, NOT} is universal. It can be demonstrated that the reduced sets [AND, NOT] and [OR, NOT] are universal, too. Going further, the reduced sets [NAND] and [NOR] are universal, meaning that the only required Boolean operations that are necessary to implement all Boolean operations are the NAND or NOR operations. However, as bitwise operations are not difficult to implement in hardware and are often used in computations, a broader set of operations ( generally [NOT, AND, OR, XOR]) is available in all modern processors for optimization purposes.

Symbols and Characters

Additionally, multiple bits may be used to represent a symbol or a text character for example, but it is then purely a usage convention based on e a specific encoding (such as ASCII or UTF-8) and does not involve any particular calculation or interpretation from the point of view of the processor.

Putting it all together

So far, so good: an ALU could be implemented with only an n-bit subtractor and either NAND or NOR logic operations.

Actually, we could optimize it further to only an n-bit subtractor and a NOT logic operation if we do not consider bitwise-operations, and we would obtain an ALU similar to the one used in h the first computer, the Manchester Mark I, or to the ongoing 8-bit TTL CPU Hackaday project Hackaday project!

Being even more extreme, we could argue that the n-bit subtractor could be implemented from logic operations (refer to the last example in Shannon's paper above) and the ALU could then be limited to a succession of NAND or NOR logic operations.

Then, as a NAND or NOR logic operation can be simulated by addressing 4 consecutive memory locations containing the equivalent truth table (1, 1, 1, 0) or (1, 0, 0, 0), the ALU could then be limited to... a single memory register, as demonstrated by Raùl Rojas in his 2010 paper "The smallest Arithmetic Logic Unit"!

Although this is an interesting result for abstract machine theory, real-world computer implement a larger set of hardware primitive functions to obtain a better efficiency:

• CLR: clear all bits
• ADD: arithmetic addition
• SUB: arithmetic subtraction
• NOT: 1's complement bitwise logic negation
• AND: bitwise logical and
• OR: bitwise logical or
• XOR: bitwise logical exclusive or
• at least one of ASL or LSL: arithmetic or logical bitwise shift left
• at least one of ASR or LSR: :arithmetic or logical bitwise shift right

This primitive operation set is often completed by derived operations, such as:

• NEG: arithmetic 2's complement, i.e. performing NOT and ADDing 1
• INC: arithmetic increment by 1
• DEC: arithmetic decrement by 1
• ROL: logical bitwise rotate left
• ROR: logical bitwise rotate right

Very often, arithmetic and rotations operations are derived in variants that include an input carry bit:

• ADC: arithmetic addition with carry
• SBC: arithmetic subtraction with carry (or borrow)
• RLC: logical bitwise rotate left through carry
• RRC: logical bitwise rotate right through carry

At the expense of a large increase in complexity, modern processor also include hardware-based signed and unsigned multiplication and division operations, and processing of non-integer numbers using floating -point arithmetic in a specialized hardware floating-point unit (FPU).

For our educational purpose, we will limit ourselves to a simple n-bit integer ALU only without hardware-based arithmetic multiplication or division that can be emulated in software.

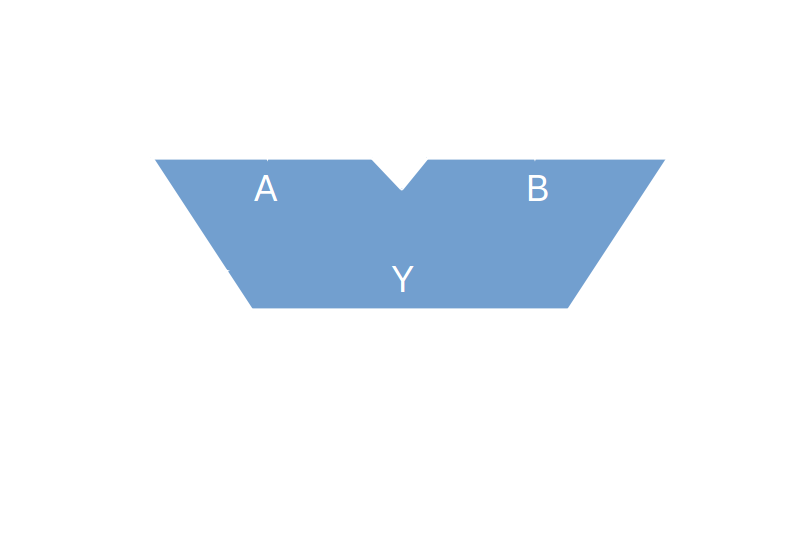
Condition Flags

In order to give algorithms the ability to behave differently, based on the result of previous calculations, the ALU must at least provide a single-bit storage (or flag) for a simple logic condition.

Theoretically, only a single condition is necessary, and the most obvious condition is nullity, i.e. a condition obtained when the last arithmetic calculation resulted in a null (zero) result. It is very common to call this condition flag Z, and to add some additional significant ones:

• Z: the last arithmetic operation resulted in a null (zero) result
• N: the last arithmetic operation resulted in a negative result (i.e. a value with its most significant bit set to 1)
• C: the last arithmetic operation generated an output carry
• V: the last arithmetic operation generated a signed number overflow (i.e. when the carry input and output for the most significant bit is different, resulting in a 2's complement wrap around)

Whenever applicable, these flags are often updated for logical bitwise operations, in order for algorithms to test bitwise conditions too.

As the ALU takes 2 integer operands and produces 1 single integer result, with the operation to perform encoded into an opcode, and that it also depends on input status flags and generates some output status flags, it is often represented as a V-shaped block like this:

At the same time as defining the central role of the processor (CPU), the evolution of memory technologies provided a random-access capability that departed from the model of the Universal Turing Machine which is based on an infinite tape as its main storage unit.

As Hao Wang wrote in 1954 in his paper "A Variant to Turing's Theory of Computing Machines" (unfortunately, behind a paywall):

Turing's theory of computable functions antedated but has not much influenced the extensive actual construction of digital computers. These two aspects of theory and practice have been developed almost entirely independently of each other. The main reason is undoubtedly that logicians are interested in questions radically different from those with which the applied mathematicians and electrical engineers are primarily concerned. It cannot, however, fail to strike one as rather strange that often the same concepts are expressed by very different terms in the two developments

Interestingly though, is the fact that Turing himself worked on both the theoretical and practical aspects of computers.

As a matter of fact, the theory of computational complexity was founded in the early 1960s only, when scheming minimal universal Turing machines has been a mental sport for years (check Peter van Emde Boas's paper "Machine Models and Simulations" for a good enumeration and classification of abstract machines).

Von Neumann (Princeton) Architecture

Both von Neumann's "First Draft of a Report on the EDVAC" and Turing's own "Proposal for Development in the Mathematics Division of an Automatic Computing Engine (ACE)" early papers describe a computer architecture that seems completely unconnected to the concept of Universal Turing Machine at first sight.

First, the fact that the machine is a serial computer that processes each instruction and data atomic components sequentially rather than all at once as in today's parallel-word computers makes it difficult to understand. But this choice does not influence the logical architecture per se, it is rather a compromise due to the technology available at that time with the sequential acoustic mercury delay line memories. With the practical availability of random-access memories of higher capacities such as the iconoscope and Williams tube, Arthur Burks, Herman H. Goldstine and John von Neumann published only one year later on 28 June 1946 the first edition of their famous paper "Preliminary discussion of the logical design of an electronic computing device" (followed on 2 September 1947 by a second edition), where a more modern design based on a parallel-word architecture is described.

Second, is the more important substitution of the sequential tape by a random-access memory and registers.

This architecture, known as the Von Neumann or Princeton architecture, was only categorized theoretically much later (in October 1964 by Calvin Elgot and Abraham Robinson in "Random-Access Stored-Program Machines, an Approach to Programming Languages", unfortunately behind a paywall) as an example implementation of a specific class of abstract register Turing-equivalent machine: the Random-Access Stored-Program (RASP) machine.

Although attributed to von Neumann alone, there is a large controversy about the fact that all the ideas exposed in this paper are his own.

There are at least some details that tend to prove that his ideas did not come ex nihilo: in section 5.3 of the Burks, Goldstine and von Neumann paper:

Several of the digital computers being built or planned in this country and England are to contain a so-called "floating decimal point"

This proves that they were aware of at least Bell labs's Mark V computer and National Physical Laboratory, UK's Pilot ACE development at that time.

In fact, there were many direct contacts between the British and American laboratories, showing that exchanges between the concurrent projects was not uncommon at this time:

• Newman from the Victoria University of Manchester (who later built the Manchester Baby) wrote to von Neumann on 8 February 1946
• Turing visited the US on January 1-20 1947, writing: "My visit to the U.S.A has not brought any very important new technical information to light, largely, I think, because the Americans have kept us so well informed during the last year"
• Harry Huskey, who worked on the ENIAC, took a sabbatical year in 1947 at the ACE section of Mathematics Division at NPL, UK

Whatever were von Neumann motivations, disclosing the computer architecture early in such public documents prevented the various people working on these projects to further patent anything they worked on, and had the positive result of placing the computer invention into the public domain.

What is remarkable though, is that the von Neumann architecture closely follows Turing's stored-program computer model, to the point where both concepts are often confused. Having a stored-program capability was mandatory for those primitive computers, which had only very poor means of specifying the data they were working on, using only:

• immediate values, part of the instruction, which only provide a calculation log capability
• absolute addresses of values, part of the instruction too, which bring an elementary algebra equivalent of variables and one level of abstraction for accessing the values

It was then impossible to address blocks of data to process, unless the program was able to self-modify itself by computing instructions with pre-computed addresses to be executed further in the algorithm, thus the stored-program condition.

Harvard Architecture

However, the stored-program model is not a strict requirement for a computer to be universal: a simple design with a looping external program capable of indirect addressing (i.e. having instructions containing the address of the address of values or two levels of abstraction for accessing the values) suffices to simulate a universal Turing machine (see the paper from Raùl Rojas "Conditional Branching is not Necessary for Universal Computation in von Neumann Computers").

The architecture that matches this description is called the Harvard Architecture, in reference to the Harvard Mark I and II built for IBM by Howard Aiken in 1944-47. These machines were not capable of universal computation, missing the indirect addressing mode, but feature a split memory for program and data.

One distinctive advantage of the Harvard Architecture compared to von Neumann's was that the CPU can both read an instruction and perform a data memory access at the same time, whereas a von Neumann architecture will be limited by the Von Neumann bottleneck. But this performance limitation is mitigated in today's computers by using:

• A cache between the CPU and the main memory
• Separate caches or access paths for data and instructions (Modified Harvard Architecture)
• Branch predictor algorithms and logic
• A limited CPU stack or on-chip scratchpad memory to reduce memory access

Pure Harvard Architecture is still used today in cache-less processors, such as Digital Signal Processors (DSPs) and some small microcontrollers.

Stack Architecture

Another popular computer architecture is the Stack Architecture, where a pushdown stack is used to store data and instructions rather than registers. Most of its instructions assume that operands will be from the stack, and results placed in the stack.

Because of the lack of addressing in the instructions, the object code is very compact. And as algebraic expressions are directly convertible into a binary syntax tree, itself easy to convert into stack-based instructions, the stack architecture permits simple compilers and interpreters to be generated. However, the stack architecture suffers from several flaws.

Only a few processors using the stack architecture were actually built, but this architecture is commonly used for Virtual Machines interpreted in software.

Transport Triggered Architecture

One last computer architecture of interest is the Transport Triggered Architecture, where computation happens as a side effect of data transport: accessing some addresses in memory triggers a functional unit to start computation. Put into other terms, the processor only features a single instruction to move data between a source and a destination, and the instruction to perform depends on the actual addresses that are accessed.

Although this architecture greatly simplifies the control logic of the processor, only a few commercial processors actually uses it:

• Maxim Integrated's MAXQ processor
• ARM Limited's MALI 200 and 400 Graphics Processing Units (GPUs)

To summarize all that, today most computers use the von Neumann Architecture with a cache, a Modified Harvard Architecture with separate instruction and data caches or access paths, with an exception for DSPs or small microcontrollers that still use a pure Harvard Architecture.

The Universal Turing Machine is a great and simple abstract structure, but is not really efficient to build a physical stored-program computer. The theoretical infinite tape model is not possible to implement in practice, and anyway, having a tape running back and forth is far from optimal for a physical storage medium.

But the Turing machine was an abstract machine invented before the physical computer existed, and was intended to represent a virtual person executing a well known procedure, not as a physical implementation model.

Clearly, the biggest challenge of the early computers was the memory capacity, and although Babbage's Analytical Engine was designed around 1835 to hold 1,000 numbers of 40 decimal digits each in a set of mechanical wheels, and flip-flops made up of purely electronic vacuum tubes were discovered back in 1920, tapes and punched cards were at that time (end of WWII) among the storage media with the best information density.

Flip-flops on the other hand required to use 2 triodes to store a single binary digit, making them unpractical except for small amounts of storage, such as intermediate results, in what we would called today registers.

In the "First Draft of a Report on the EDVAC" and attributed to Von Neumann was the first description of possible solutions to get a larger storage capacity using acoustic mercury delay line memories that were able to store 1,000 binary digits, and video camera tubes called iconoscopes, able to store up to an estimated 250,000 binary digits. At the same time, this paper introduced the concept of Random-Access Memory (RAM) for the first time. The first stored-program computer, the Manchester Baby, used a variant of the iconoscope, the Williams tube, to store 2,048 binary digits in a 64 x 32 array.

This increase in storage memory capacities led to a clearer subdivision of the computer system as a whole. In the "First Draft of a Report on the EDVAC", Von Neumann distinguished:

1. A Central Arithmetical part (CA)
2. A Central Control (CC)
3. Memory (M)
4. An outside Recording medium (R)
5. An Input (I)
6. An Output (O)

With (C) defined as being CA and CC (i.e. the Central Arithmetical and Central Control parts) put together.

In "Proposal for Development in the Mathematics Division of an Automatic Computing Engine (ACE)", Turing details:

1. A Dynamic Storage (DS)
2. Temporary Storage (TS)
3. An Input Organ (IO)
4. An Output Organ (OO)
5. A Logical Control (LC)
6. A Central Arithmetic part (CA)
7. Various 'trees" required in connection with LC and CA for the selection of the information required at any moment
8. A Clock (CL)
9. A Temperature control system for the delay lines
10. Binary to decimal and decimal to binary converters
11. A Starting device
12. A power supply

And although the Temporary Storage could be seen today as equivalent to RISC processor register banks, the explicit notion of processor is not clearly stated in his paper. But Turing himself admitted in 1947 that "[digital computing] Machines such as the ACE may be regarded as practical versions of this same type of [universal] machines. There is at least a very close analogy. Digital computing machines all have a central mechanism or control and some very extensive form of memory".

Since then, the vast majority of modern computer feature a Central Processing Unit or CPU, also simply called processor, composed of a control unit and an arithmetic unit.

The second and last post on computer history...

For a long time, the first physical digital computer was considered to be the ENIAC, but this is no longer considered true.

Source:TexasDex at English Wikipedia GFDL or CC-BY-SA-3.0, via Wikimedia Commons

It was not until the 70s that the fact that electronic computation had been used successfully during WWII by the Government Code and Cypher School (GC&CS) at Bletchley Park was acknowledged, where Turing played a major role by designing the electromechanical cryptologic bomb used for speeding up the codebreaking of the German Enigma machine.

Source: Karsten Sperling, http://spiff.de/photo

And it was not until 1983 that details on the hardware of the Colossus I machine used later during the war (February 1944) were declassified. Other details were held secret until 1986, and even today, some documents remain classified.

Source: See page for author [Public domain], via Wikimedia Commons

This machine was used to decipher messages from the Lorenz cipher machine used by the German High Command, and Turing was involved in it at least for some of the methods used to perform wheel-breaking, but also by recommending Tommy Flowers (with whom he worked on the bomb) to Max Newman, if not some other yet undocumented implications.

To add to this complexity, Turing also had contacts as soon as in 1935-1938 during his Princeton years with John von Neumann who worked later on the ENIAC and the EDVAC, during his research for the first atomic bomb.

Source: See page for author [Public domain], via Wikimedia Commons

Because of this secrecy around Bletchley Park operation and later because of the revelation of Turing's homosexuality and death, it is very difficult to find out the truth regarding the first physical digital computer: having heroes and wise generals on the battlefield was considered for a long time to be a better image of victory during WWII than mathematicians in a dark room...

F.H. Hinsley, official historian of GC&CS, has estimated that "the war in Europe was shortened by at least two years as a result of the signals intelligence operation carried out at Bletchley Park". But it may well be underestimated: if you consider that the Lorentz cipher was routinely cracked in July 1942 (the first battle of El Alamein was 1-27 July 1942) when for the first time the German troops were defeated, and the Mark I Colossus started its operation in February 1944 (just before D-Day), it may well be that it actually changed the war.

Even worse, Turing's personal situation lead to strange rewriting of some part of History, amnesia, minimization of his role, if not complete credit re-attributions.

But neither the Colossus nor the ENIAC could be actually considered as the first physical digital computer, both storing programs differently from numbers, and in this regards, were just massive electronic calculating machines.

The first specification of an electronic stored-program general-purpose digital computer is von Neumann's "First Draft of a Report on the EDVAC" (dated May 1945) and contained little engineering detail, followed shortly by Turing's "Proposal for Development in the Mathematics Division of an Automatic Computing Engine (ACE)" (dated October-December 1945), which provided a relatively more complete specification.

However, the EDVAC was only completed 6 years later (and not by von Neumann), and Turing left the National Physical Laboratory (NPL) in London in 1948, before a small pilot model of the Automatic Computing Engine was achieved in May 1950. He then joined Max Newman in September 1948 at the Royal Society Computing Machine Laboratory at Manchester University.

This is where the Manchester Small-Scale Experimental Machine (SSEM), nicknamed Baby, ran its first program on the 21^st June 1948 and became the world's first stored-program computer. It was built by Frederic C. Williams, Tom Kilburn and Geoff Tootill, who reported it in a letter to the Journal Nature published in September 1948.

Source: By Parrot of Doom (Own work) [CC BY-SA 3.0 or GFDL], via Wikimedia Commons

This prototype machine quickly led to the construction of the more practical Manchester Mark 1 computer which was operational in April 1949.

In turn, it led to the development of the Ferranti Mark 1 computer, considered as the world's first commercially available general-purpose computer in February 1951.

However, Turing's shadow still floats over the Manchester computers, since Williams is explicit concerning Turing's role and gives something of the flavor of the explanation that he and Kilburn received:

'Tom Kilburn and I knew nothing about computers, but a lot about circuits. Professor Newman and Mr A.M. Turing in the Mathematics Department knew a lot about computers and substantially nothing about electronics. They took us by the hand and explained how numbers could live in houses with addresses and how if they did they could be kept track of during a calculation.' (Williams, F.C. 'Early Computers at Manchester University' The Radio and Electronic Engineer, 45 (1975): 237-331, p. 328.)'

Turing did not write the first program to run on the Manchester Baby, but the third, to carry out long division, and later developed an optimized algorithm to compute Mersenne prime, known as the "Mersenne Express" for the Manchester Mark 1 computer.

Today, digital computers are everywhere: not only on our desktops, but also in the palm of our hand as a smartphone, or behind the dashboard of our car. However, this situation is not very old: the first personal computers appeared in the late 70's, mobile phones at the turn of the century, and smartphones only 10 years ago with the first iPhone. Actually, this acceleration is rather unique, since computers only appeared with WW II.

But as far as can be traced back in History, humankind used means to represent or count items: livestock, grains, etc. First using the fingers, then stones, rods, abacus and numerous other aids.

Other specialized devices (such as astrolabe, the Antikythera mechanism or clock towers) were invented to compute astronomical positions or for navigation use.

Eventually, more general purpose devices were built in order to perform arbitrary sets of arithmetic or logical operations, like slide rules or (electro-)mechanical calculators.

And despite the fact that some of these machines (like Jacquard's loom, which used punched cards to control pattern being woven) introduced the notion of programmability, they cannot be considered as computers, since it applied to machine tools and not to general arithmetic or logical operations. The term of computer was used since the early 17th century to designate human computers performing long and tedious mathematical calculations.

What would have been the first general-purpose computer is the Analytical Engine, proposed by Charles Babbage in 1834:

Source: Bruno Barral (ByB) CC BY-SA 2.5, via Wikimedia Commons

But unfortunately, this computer was never completed.

Instead, at the turn of the 20th century, and because of their lower complexity, many computing machines were based on direct mapping of values to continuous physical phenomena such as electrical, mechanical or hydraulic quantities. However, because of the measurement accuracy and inherent random jitter added by various uncontrolled phenomenon, processes could not be reliably repeated with exact equivalence on these analog computers.

In contrast, digital computers (from Latin digitus, finger) use sets of discrete symbols to represent values, and because of this indirect mapping, they are able to have repeatable results with no accuracy or random noise problem.

And it was only in 1936 in his famous paper "On Computable Numbers, with an Application to the Entscheidungsproblem" that Alan Turing first described a class of digital computing machines now known as Turing machines. Being kind of odd by today's standards, a Turing machine can be considered having 3 distinct elements:

1. an infinite tape, divided into a sequence of squares, each carrying a symbol from a finite alphabet
2. a read/write head that can read the symbol contained in one single square of the tape at a time, write a new symbol there and move one square to the left or to the right
3. a control element as a device with a finite number of internal states

At any given time, the next operation of the Turing machine is determined by:

1. the control element's current state
2. the symbol read by the read head

The operation consists in 3 parts:

1. print a new symbol int the current square on the tape (it may be the same as the read symbol)
2. put the control element into a new state (which may be the same as the previous state)
3. move the read/write head one square to the left or to the right

For its operation, a finite part of the tape is filled with a starting sequence of symbols, the remainder of the tape being left blank (containing a special blank symbol), and the read/write head is placed at a particular starting square on the tape. The Turing machine then starts to compute following its rules of operation.

Source: wvbailey (Own work) GFDL or CC BY-SA 3.0, via Wikimedia Commons

Despite its singular construction, the Turing machine model captures for the first time the notions of:

1. algorithm as a self-contained sequence of actions to be performed in the control element's internal states
2. sequential memory under the form of its infinite tape
3. processor as a Turing machine controls all data manipulation done by a digital computer

In his paper, Turing also demonstrated that it is possible to design a Universal Turing Machine (UTM) that can act like any particular Turing machine when supplied with a description of that machine placed on the tape of the UTM using a certain code and starting sequence of the particular Turing machine, in which case the UTM will imitate the operation of the particular Turing machine. This reduces the problem of simulating all particular Turing machines to the problem of simulating only any UTM.

Source: By Cbuckley (Own work) GFDL or CC-BY-SA-3.0, via Wikimedia Commons

Thus, the UTM may be considered as the first implementation of an interpretive routine or alternatively, as the first stored-program computer, where programs not only operate on numbers, but are represented themselves as numbers.

However, Turing machines are not limited to model computers, but rather they are intended to model abstract computation itself. For example, it is very possible for a Turing Machine to model human computation process. Historically, computers, which compute only on their (fixed) internal storage, were developed only later. But except for the limitations imposed by their finite memory stores, modern computers are said to be Turing-complete, i.e. they have algorithm execution capability equivalent to a Universal Turing Machine.

As a conclusion, it can be observed that modern computers differs mainly from abstract Turing machines in that they only have a finite memory capacity, but that they share the ability to follow an algorithm using a processing unit and memory for storing both data and instructions. For practical purposes, real-world computers also add some data input/output capabilities in order to be useful for an application.