Rune
There is a lot of information on the internet about this problem, and the first way I was trying to solve the problem with was Ant Colony Optimization (ACO). But after implementing it I realized that is was not very fast, and the resulting route wasn'toptimized very good.This could the due to I haven't used the most optimal parameter settings for the problem I was solving at the time.But because this algorithm have parameter, that they should be changed after a given problem is a major drawback. So I changed to a 2-opt kernighan–Lin algorithm.
The algorithm used:
The 2-opt algorithm is very simple and works by switching two paths to make the tour shorter. As shown here:
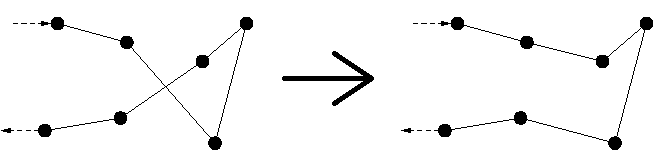
The algorithm is going through all possible swaps, and by replacing only the shorter swaps with to the tour. Resulting in a shorter and shorter tour, and when the tour can't get any shorter it stops and your have found the optimum tour with this algorithm.
The code I made to this algorithm was surprisingly simple, faster and give more optimum tour than the Ant Colony Optimization. So here it is:
int[] opt2(int[] path, double[][] dis)
{
int cities = dis.GetLength(0), i, j;
START:
for (i = 0; i < cities - 2; i++)
{
for (j = i + 2; j < cities; j++)
{
double swap_length = dis[path[i]][path[j]] +
dis[path[i + 1]][path[j + 1]];
double old_length = dis[path[i]][path[i + 1]] +
dis[path[j]][path[j + 1]];
if (swap_length < old_length)
{
// Make the new and shorter path.
for (int x = 0; x < (j - i) / 2; x++)
{
int temp = path[i + 1 + x];
path[i + 1 + x] = path[j - x];
path[j - x] = temp;
}
goto START;
}
}
}
return path;
}This function has 2 input parameters :
int[] path : An array that represent the current path(tour).
Ex. path = {0,2,1,0} is a tour that goes form city 0 to - 2 - 1 - 0.
double[][] dis : Is an array of arrays where the row index represent the city your are coming from and the column index represent the city you are going to.
Ex. dis[0][2] = gives the distance from city 0 to city 2.
The return parameter is the optimized tour.
Todd
agp.cooper
Carl Strathearn
Hi one more time,
I finished coding my version of the g-Code optimiser and a surprising result.
Some Background
I use Vectric Cut2D v1.5 as my CAM software and I noticed that the output order was rather "random" in that it was neither left to right nor top to bottom nor in order of creation, etc.
In fact it would do half a group of letters, then go away and then come back to finish the text.
So okay I thought I could clean this up using the Travelling Salesman Algorithm (TSA).
The Result
I have some working code (checks out mathematically against test data and graphically as valid) but it is 20% worse than the Cut2D gCode!?
Well the answer is that the Cut2D gCode has already been optimised using a better TSA than mine. The reason for the apparent random lettering is that the Cut2D gCode is a good solution but not an optimal solution (which is expected as optimal solutions are very hard to solve) and we are both using approximate solution algorithms.
So an interesting exercise but a fatally flawed premise.
I would appear to me that practically all CAM software probably outputs a TSA solution for its gCode (obviously I have not checked). It just looks "random" the naive eye.
My code also filters out redundant points based on a tolerance parameter so not everything was wasted (Cut2D v1.5 does not do that).
Regards Alan