In the context I am using this in means that a person ages differently on different planets due to the space-time fabric bending differently on that planet. We typically measure our age in years on Earth. This increments every time the earth completes a revolution around the sun. Gravitational time dilation implies that the actual rate we age in the time it takes the earth to rotate the sun will be different depending on where we are at in the universe. I haven't found much published research other than what is shown here and in the references. This third set will be a tough egg to crack; I will attempt it after I build the second type of clock. One can now imagine a 2 column by 8 row clock. The first column would show the time on each planet at the 0 degree point; similar to the time at the prime meridian on our planet. The second column would show how old you are given the space-time distortion on that planet. In this project I'm not going to address the first case. I will address the second and third cases because they are more interesting. Also because I couldn't find any information in this area so I thought I would work through it here. I cool result of all this would also be a set of probes sent to each planet in our solar system. The probe would simply report back the time on that planet. It would need to be an atomic clock of some sort so that we could measure the relative differences in space time between our planet and the other planets.
I'm going to address the second case first. This is the case where we do a 24 hour time base transform for each planet. I need to first understand how long one earth second is compared to a second on any other planets in our solar system. The rotational velocity for each planet is the major piece of information. I built a table for this. The table has links to NASA's planet home page and Wikipedia's home page since NASA doesn't have the rotational velocity information immediately available.
| Planet | Equatorial rotation velocity (m/s) |
| Mercury | 3.026 |
| Venus | 1.81 |
| Earth | 465.1 |
| Mars | 241.17 |
| Jupiter | 12600 |
| Saturn | 9870 |
| Uranus | 2590 |
| Neptune | 2680 |
What this really says is how far the planet spins in 1 earth second. One of many assumptions I will make here is that each planet is a circle at it's equator. This means that one of normalizing factors I can use is the amount of degrees a planet moves. This amount can then be used for the transform to find one second on a given planet. For this measurement I'll need the mean radius. Here I look at the minimum radius so there is some error introduced. Since there is a range I can make this more accurate in the future my making an average or another similar model of the radius to estimate the second. The big picture here is a unit's game with the goal to find the frequency in Hertz for a given planets revolution.
| Planet | Mean Radius (min) |
| Mercury | 2438700 |
| Venus | 6050800 |
| Earth | 6371000 |
| Mars | 3389300 |
| Jupiter | 6990500 |
| Saturn | 5822600 |
| Uranus | 2460300 |
| Neptune | 2535500 |
Now I need to understand how many degrees and radians the earth turns in one second. Since this was a simple calculation I made a table for it as well
| On Earth | Metric |
| Degrees in a circle | 360 |
| Day/Degree | 0.002777777778 |
| Hours/Degree | 0.06666666667 |
| Minute/Degree | 4 |
| Seconds/Degree | 240 |
| Degrees in a second | 0.004166666667 |
| Radians in a second | 0.00007272205217 |
Now there is a formula to find out the arc length is for the each planet with a given radius. The Wikipedia article gives the best description of this calculation:
Arcs of circlesArc lengths are denoted by s, since the Latin word for length (or size) is spatium.
In the following lines,represents the radius of a circle,
is its diameter,
is its circumference,
is the length of an arc of the circle, and
is the angle which the arc subtends at the centre of the circle. The distances
and
are expressed in the same units.
![C=2\pi r,]() which is the same as
which is the same as ![C=\pi d.]() (This equation is a definition of
(This equation is a definition of ![\pi]() (pi).)
(pi).)- If the arc is a semicircle, then
![s=\pi r.]()
- If
![\theta]() is in radians then
is in radians then ![s =r\theta.]() (This is a definition of the radian.)
(This is a definition of the radian.) - If
![\theta]() is in degrees, then
is in degrees, then ![s=\frac{\pi r \theta}{180},]() which is the same as
which is the same as ![s=\frac{C \theta}{360}.]()
- If...
 shane kirkbride
shane kirkbride represents the
represents the 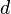 is its
is its 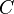 is its
is its  is the length of an arc of the circle, and
is the length of an arc of the circle, and  is the angle which the arc subtends at the
is the angle which the arc subtends at the  and
and  which is the same as
which is the same as  (This equation is a definition of
(This equation is a definition of 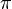 (
(
 (This is a definition of the radian.)
(This is a definition of the radian.) which is the same as
which is the same as 


Hi
Nice to meet you after viewing your profile i am Jacinda, from (jakarta) indonesia,
i have a project discussion with you please email me on: (jacinda.seiler@yahoo.com)