The third component of Firefly's algorithmic layer deals with the problem of autonomously locating a target—like a trapped victim after a disaster or the source of a fire in a burning building—by combining multiple different sensory inputs. The problem with existing approaches is that they largely focus on taking measurements in several, precise locations, using these measurements to compute the location of the target.
Approach 1: Reinforcement Learning
Initially, this seemed like a classic reinforcement learning problem, because it's easy to formulate the problem in terms of states (sensor readings), actions (robot behaviors), and rewards (when you get closer to the target). I implemented this on my first prototype of Firefly—here are my notes:

While this approach sounded good in theory, there were a few problems that made it infeasible. First, it required extensive training for each use case. It also didn't generalize well; I found that it worked only in the specific cases for which it was trained. Additionally, it wasn't robust to noisy sensor readings, which was especially problematic because I was using very cheap sensors that produced a useful output but also had significant noise. Because of this, I quickly decided to move on to a simpler, behavior-based approach, described below.
Approach 2: Following Multiple Gradients
This approach worked much more reliably, both in simulation (see below) and in some real-world experiments. Here's a graphic I made giving an overview of this approach:

Evaluation
I created a simulation to see how this algorithm would perform in a variety of environments. In the simulation, the robot starts out with a random position and orientation inside a square arena (with a certain side length) or circular arena (with a certain diameter) and moves 0.1 meters per loop iteration. The arena contains four identical obstacles with random orientations; the robot has to avoid these obstacles and the arena walls. Concentration and temperature are modeled with a two-dimensional Gaussian distribution centered in the arena; the distribution for concentration fills the arena, while the distribution for temperature is limited to a small area around the target.
You can see the results of a few simulation runs above (they're the diagrams at the bottom of the image). I also used the simulation to quantify the effectiveness of this algorithm, and I was very happy with the results—the simulation indicated that the algorithm is effective (~98% success rate given the ten-minute flight time of a typical quadrotor), efficient, and scales well to large environments. Here are some specifics on what I found: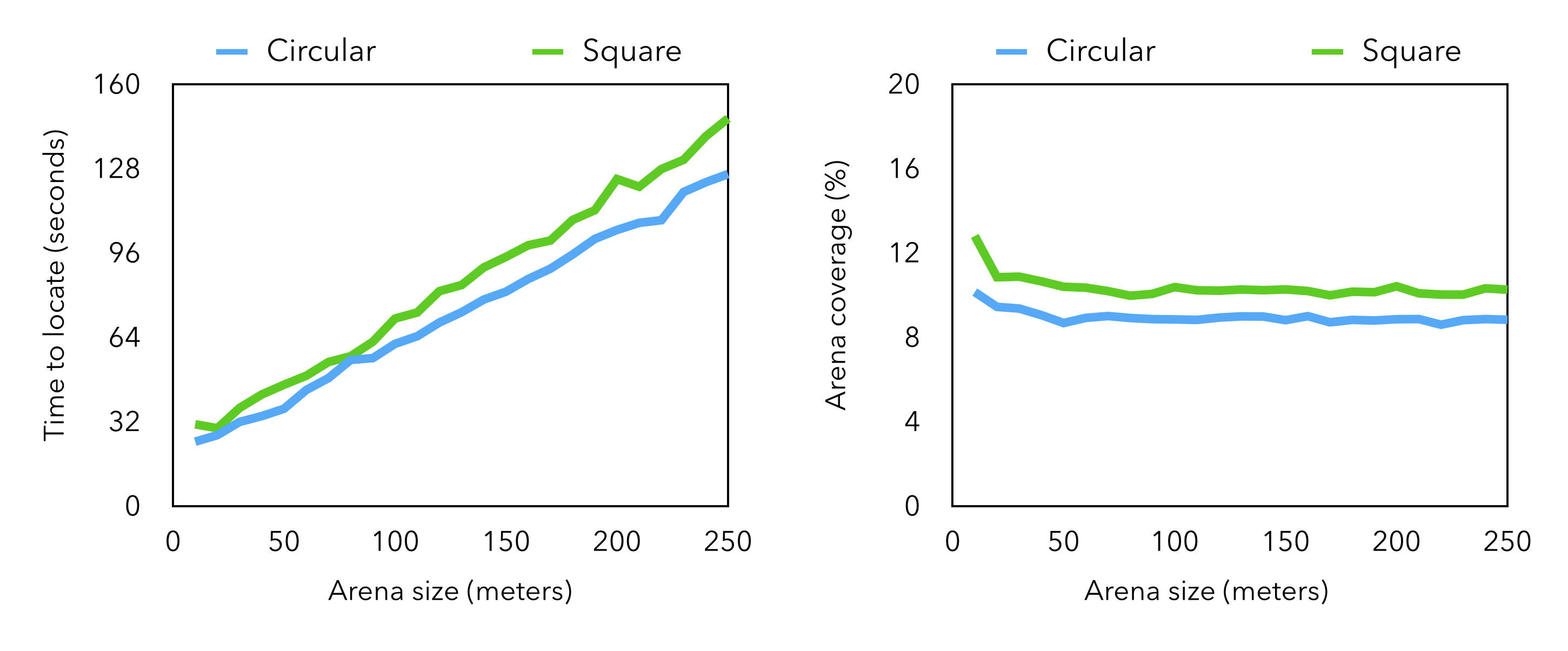 I also conducted some real-world testing with a group of local firefighters—I'll talk more about that in a future log. Until then, if you want to see the algorithm in action, my TEDxTeen talk (linked in the sidebar) includes a video of one of these experiments.
I also conducted some real-world testing with a group of local firefighters—I'll talk more about that in a future log. Until then, if you want to see the algorithm in action, my TEDxTeen talk (linked in the sidebar) includes a video of one of these experiments.
 Mihir Garimella
Mihir Garimella
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.