Jana Marie
How it works:
We choose an axiom, for example: 'A'
Now we have rules like: "A becomes AF" and "F becomes FA"
Next step is to iterate the axiom through the rules by an specific amount, the output will be fed through the rules again.
For example we iterate 3 times:
A -> AF
AF -> AFFA
AFFA -> AFFAFAAF
Our result string is now AFFAFAAF
The next step is to process the string onto our screen, for this we also have a few rules, these are:
# F,A = move n forward
# G = move n forward without drawing a line
# B = move n backwards
# - = turn left by angle
# + = turn right by angle
# [ = push position and angle
# ] = pop position and angle
# a,b,c,d = color 1,2,3,4
# 1-4 line size (std = 1) # other = variables
The processing of the string works by checking char for char against the processing rules and do what they say. If we have something that doesn't fit any rules, it doesn't matter, we will just ignore it.
Processing the upper string would be lame, it will create a straight line...
Lets add a few more interesting chars to the production rules:
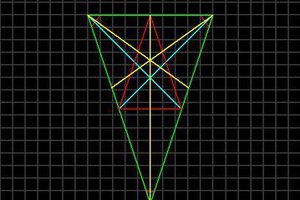
F -> a2FF-[c1-F+F+F]+[c1+F-F-F]
axiom: F
angle: 23
iteration: 5
Well, that looks a little bit more complicated and it is. This production rule contains nearly every possible processing rule and will create a colored tree with different sized lines.
the resulting string looks like this:
And the processed image like this:
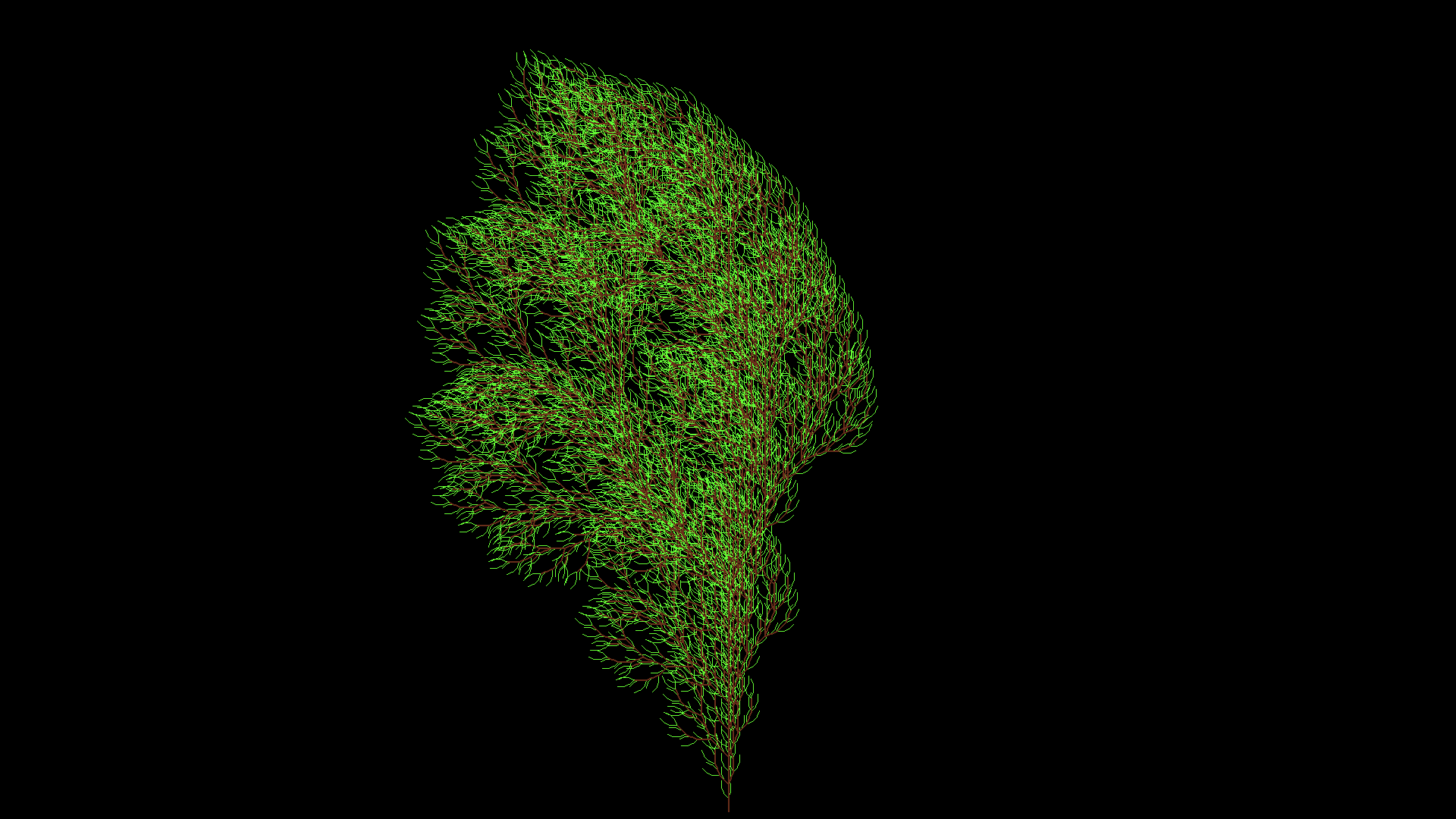
Furthermore we can play with the rules and also have multiple rules at the same time, that can result in fancy images like the Dragoncurve:
The rules are:
X -> X+YF+
Y -> -FX-Y
axiom: FX
angle: 90
You can find a set of rules in the python program.
Another example:
Wheat \o/
rules['F'] = 'F[+F]F[-F]F'
Toby
glgorman
jeroen
Maave