-
Back in the days
12/14/2018 at 19:44 • 0 commentsENIAC is often credited for being "the first calculator" but "real computers" emerged very soon afterwards, following the famous "Von Neumann report". Today, I just found details about the WhirlWind : https://medium.com/chmcore/the-whirlwind-computer-at-chm-dab505bc52a6 and the structure is "very interesting" !
![]()
This means that the "bitslice" organisation can be traced back to the late 1940s, because each of the 16 racks would implement one bit of the datapath, gathering one bit from each register and the ALU. There are now many, many diagrams in this report : www.bitsavers.org/pdf/mit/whirlwind/R-series/R-127_Whirlwind_I_Computer_Block_Diagrams_Volume_2_Sep47.pdf It "feels" particularly modern and reads easily, using pretty standard conventions and using very well known structures.
-
ARM1 layout
05/25/2018 at 04:58 • 0 commentsThe co-creator of the first ARM processor explains the layout of the chip.
The "datapath" uses 3/5th at the "bottom" and it looks a lot like what I have also concluded in this project. The ALU (left) is right next to the register file, in a regular, bitslice fashion. 32 slices are stacked vertically (bit0 at the bottom). A barrel shifter is placed at the right of the ALU. This is pretty similar to what I intend to do, so I reinvented the wheel again :-D
-
Front panel...
12/22/2017 at 00:41 • 4 commentsI just found that picture on eBay, for an IBM S/34 front panel :
![]()
I have no idea what a S/34 is, BTW. Maybe a 16-bits machine ? Oh, I should have looked it up first... at http://www.corestore.org/34.htm
However I see that they use hexadecimal rotary buttons, just like the assembler board of #YGREC and that's pretty interesting ! However, is there no disassembly board ?
-
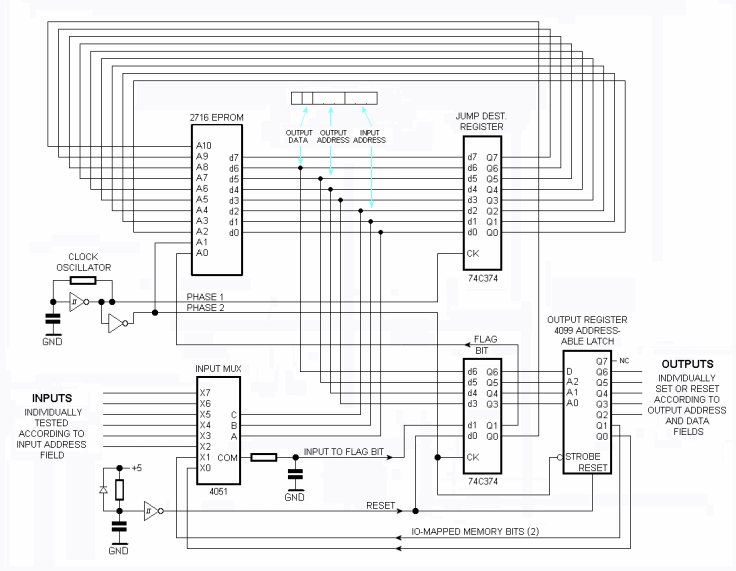
Enabling discovery
05/28/2017 at 23:20 • 2 commentsToday, I followed @BigEd's link to his forum where he describes minimalistic systems with one page.
There, I find a description of Dr Jefyll's One Bit ComputerOne Bit Computer
It's indeed reminiscent of Motorola![]()
MC14500 1-bit computers but with no special-purpose chip. All the intelligence is in the EPROM. I admire the ingenuity of this design !
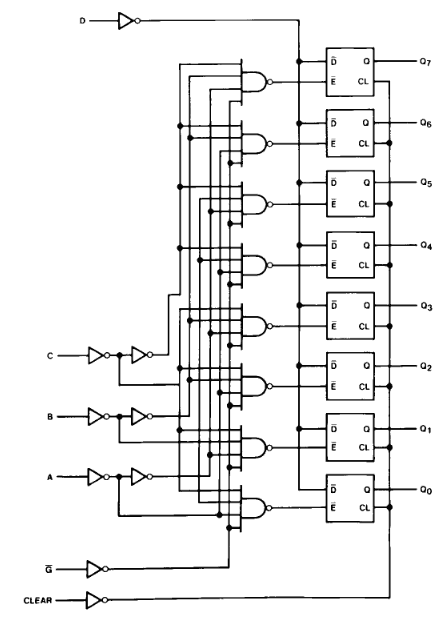
What caught my eyes though is the output register : "4099 addressable latch" that gets 3 address bits, a latch enable and a data input.
Wait.
Isn't this what I complained that I couldn't find in integrated circuits ?
I have been repeatedly suggested to make a TTL/CMOS version of AMBAP/YGREC but the big roadblock is the register set : all the registers I know are 8 bits with common clock (274, 573, 574 etc.) so a pure bitslice implementation is hard.
Finding a 1-bit wide 8-addresses SRAM chip changes everything and the 4099 maps directly to the address decoder and latches of the register set. Add a few MUX and you're done.
The 4099 however is a bit of an old relic. A lookup on Wikipedia finds however the 74259 : "8-bit addressable latch"
Right : a latch, not a FF/register, just like YGREC is intended to be: a buffer latches the result during a previous clock phase to prevent a direct feedback.![]()
The clear input is welcome but not required. It's precious however for applications as IO port extender, which I'll also consider.
So I just ordered a bunch of these chips and a CMOS YGREC is lurking on the horizon...
Thanks BigEd !
20170510:
I got convinced into creating #YGRECmos :-)
See the rest there !
-
There is another system
03/23/2017 at 20:45 • 5 comments@DL101 tells me about the Intel 3002 :
http://www.cpu-world.com/CPUs/3002/
This rings a bell, with the following differences :
- only one bit per slice for the AMBAP
- memory is linked directly to each of AMBAP's slices
- AMBAP has only 8 or 16 registers (not 11)
I need to find more documentation about this chip now... The die shot is glorious :
![]()
Thanks DL !
-
Tree balancing for IC
03/07/2017 at 14:38 • 0 commentsThe previously described method for balancing a tree of MUX relays has reminded me the difficulty of creating a similar dual-MUX tree in FPGA where there is no memory blocks. I encountered this problem while designing the YASEP in VHDL for Actel's A3P family and the buffering was pretty complicated.
In ASIC/FPGA though the partition constraints are relaxed and slight unbalances can help the place/router put gates further or closer. Furthermore, the synchronicity of the arrival of all the signals ensures a more consistent timing. The elimitation of huge final fanout also brings a better overall operating speed.
20170317
The previous research dealt with the relay version of the register set and memory decoder, which I now realize are specific cases of the Knapsack problem. I'm now diving in the realm of Combinatorial optimization!
With ASIC or FPGA, we can relax some of the constraints and a little imbalance (10% or less) is not critical. We don't even have a constraint of having a power-of-two number of sinks because the gate inputs are not in series and tied in the middle. As a consequence, for an ASIC or FPGA, the original approach of rotation is easy and makes sense !
Let's examine the example of a 16-addresses register set, such as used by the #YASEP Yet Another Small Embedded Processor or the #F-CPU (v2). There are 4 address lines, and let's consider a 16-bits wide register (wider registers are just duplicates). The total fan-in is 16+32+64+128=240 for the 16×MUX16. The problematic fan-in of 128 (the last stage of the MUX) is reduced to four fan-ins of 240/4=60. This is slightlty faster (because there are less buffers to traverse, I estimate the gain to be equivalent to 1 gate propagation time due to the propagation in forward and reverse directions) and makes a more regular structure.
Actually the structure can be decomposed in groups of bits that are as wide as the number of address lines. For our 4-addresses register set, we can create groups of 4 bits, each with a fan-in of (1+2+4+8)=15 (per bit). For a full-custom design, these nibbles can be hand-optimised then duplicated as required, but it's also possible to just let the synthesizer&place&route decide how to allocate the 4 buffer lines. I should write some VHDL for this...
20170320
Interleaving.
There is more than a way to interleave the control lines. For example, simple rotations have at least 3 versions:
step=4 step=2 step=1 0 a b c d a b c d a b c d 1 a b c d a b c d b c d a 2 a b c d b c d a c d a b 3 a b c d b c d a d a b c 4 b c d a c d a b a b c d 5 b c d a c d a b b c d a 6 b c d a d a b c c d a b 7 b c d a d a b c d a b c 8 c d a b a b c d a b c d 9 c d a b a b c d b c d a A c d a b b c d a c d a b B c d a b b c d a d a b c C d a b c c d a b a b c d D d a b c c d a b b c d a E d a b c d a b c c d a b F d a b c d a b c d a b c
I don't even mention the direction (negative steps) or miroring (dcba instead of abcd).Then there is the matter of "reversal" (using a different symmetry)...
0 a b c d 1 b c d a 2 c d a b 3 d a b c 4 d a b c 5 c d a b 6 b c d a 7 a b c d 8 a b c d 9 b c d a A c d a b B d a b c C d a b c D c d a b E b c d a F a b c dAll these combinations should be tried and tested to see which yields the best speed, considering that each FPGA or gate array has their own characteristics, fanout trees, etc..
-
Backplane routing considerations
01/22/2017 at 20:14 • 0 commentsEdit 20170402: This entry is now moot/obsolete because of the approach explained in More balanced trees !
However this log is a very very interesting discussion that can be useful for other similar cases.The last log How to balance a fanout tree has shown that it is possible to organise the coils in such a way that they are wired in strings on each (identical) bitslice board.
This greatly reduces the complexity of the boards and the number of signals on the backplane connector. OTOH this shuffles the bits all over the place and the backplane must reorder everything.
I have decided to implement parity checks over the DRAM read/write, as well as the register read/writes. There are 16+1=17 identical boards, parity is calculated on the 16 data boards and stored on the 17th board, using the bypass signals.
As a consequence, there are several "shuffled busses":
- 3 address bits for the write register
- 3 address bits for the read/I register
- 3 address bits for the read/R register
- 4 address bits for the memory line
- 5 address bits for the memory columns
(the columns are still not well defined, but must be considered and studied)
The "balanced shuffling" has been designed for 3 and 4 lines and 16 bits. However now it's 17 bits and the 5-bits shuffling is a new challenge...
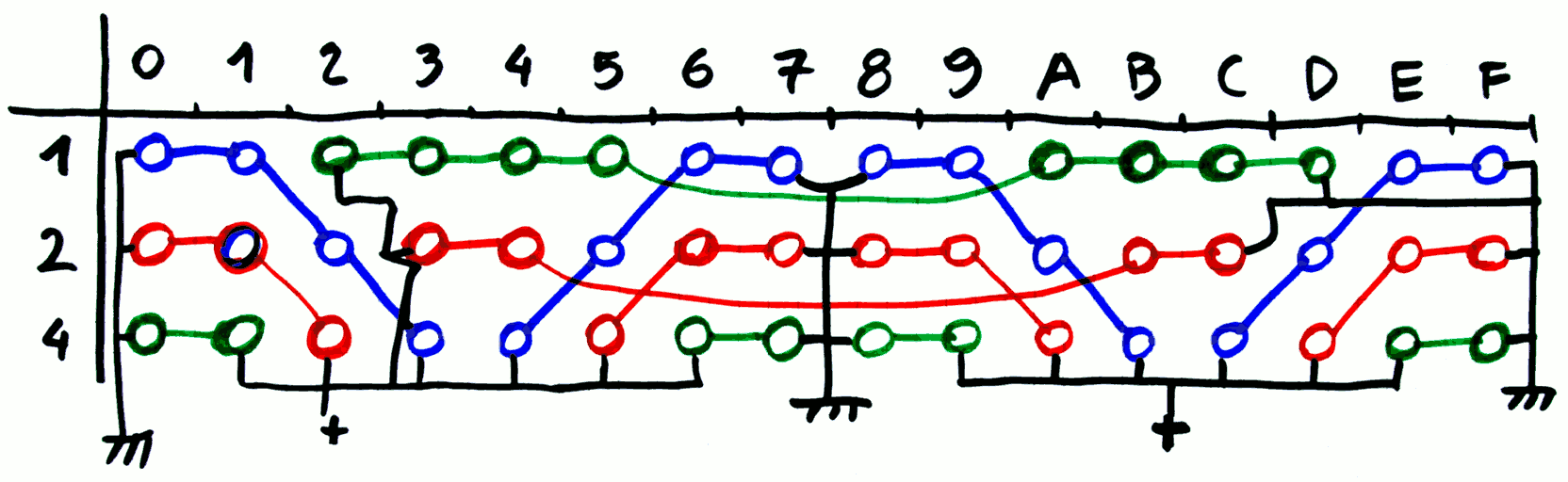
Let's start with the 3×16 balanced shuffle.
![]() There are:
There are:- 4 strings of blue
- 5 strings of green
- 5 strings of red
Then there are 3 strings of 1, 2 and 4 coils to add at the end.
But I have not yet studied the fanout of a CCPBRL gate to several 12V, 8-coils strings. So how many parallel strings can one relay drive ?
Another "EMI reduction measure" is to switch approximately one half of the coils to 12V, the other half to 24V, thus reducing the draw on the power rails and halving the decoupling capacitance.
20170320
The above routing works for 3 and 4 control lines with 16 bits, but more bits are needed and 5 control lines might become impossible to route.
17 is a prime number and does not look easy to use/partition. However the next number 18 is 2×3×3 and is great for use with "rotations" partitions. The would be one resistor per bit but that's a theoretical limit (I checked the numbers) and that's not a huge loss, the layout will be a bit less complicated.
Here are two possible routings for one half (9 bits) of the slices:
However 4 and 5 are not easy to partition with 18 bits but there is a bit of hope. A recent log "CC-PBRL : Magnetic hysteresis and fanout" has shown that strings can be 4 or 6 coils long as well.
There is another interesting thing ! Past the 3 address bits, the other lines (with 8 and 16 fanins) "behave" differently because they are integer multiples of the required string length. The partition procedure can use more heuristics and various steps to reach the required balance. For example, we can start from the address line with the highest fanin then refine...
However the numbers start to look unfavorable.
- 4 address bits: 1+2+4+8=15 fanin per bitslice, 15×18=270 fanin total, or 67.5 fanin per bit, or 8.43 strings of 8 coils per address bit
- 5 address bits: 1+2+4+8+16=31 fanin per bitslice, 31×18=558 fanin total, or 111.6 fanin per bit, or 14 strings of 8 coils per address bit
The memory decoder is going to be a MAJOR fanout problem...
20170324
Let's apply some basic logic.
It is possible to get a number that is a multiple of 3, 4 and 5 by simply multiplying them all together.
3×4×5=60 : this is not a convenient number !
3×5 = 15 : that's too low, even though making a 14-bits computer is not impossible (though slightly unpractical)
17 is prime, forget it.
18 is nice but not a multiple of 5.
How is it possible to dump this dependency on this number 5 ?
The next number is 6, which aligns neatly with 2×3 and its multiples (18...)
This number 5 comes from the 32 relays, or the 16 pairs, that steer current at the columns of the DRAM arrays. The array is a 16×16 capacitors memory, creating a 256-words addressing space. Going from 32 to 64 relays increases the memory space to 512 words (or 1Ki bytes if 16 bits are used).
....
Driving 64×18=1152 relays must create insane inrush currents and that's probably the highest fanout of this project. That's 144 strings of 8 relays, 8 strings per bitslice. I must implement a local buffer : a relay (with fan-in of 1) will drive the 8 strings of 8 relays.
This FI1 signal is naturally in series with the FI1 signal of the root's MUX2, which simplifies a rotation-based partition.
OK the above is actually wrong.
Here are the actual "shuffled busses":
- 3 address bits for the write register : Fanin 1, 2, 4
- 3 address bits for the read/I register : Fanin 1, 2, 4
- 3 address bits for the read/R register : Fanin 1, 2, 4
- 4 address bits for the memory line : Fanin 1, 2, 4, 8
- 4 address bits for the memory columns : Fanin 1, 2, 4, 16
The mistakes I made in the initial problem statement are in bold face.
The missed detail is that the final level of the column drivers is doubled : two relays are necessary to switch both diode rails of each column.
These numbers are valid for a 16×16 words array (256 words, 512 bytes). That's pretty decent (with 4K capacitors). For 18 bitslices, that's 38×18=684 decoding relays... I have already settled for 256 words because a larger DRAM bitplane would be larger than 10×10cm. I am considering stacking two DRAM bitplanes but it is appearent that this extension should not be on the columns, but the rows because the last column's relays are doubled.
Estimates for a 512 words memory :
- 5 address bits for the memory line : Fanin 1, 2, 4, 8, 16
- 4 address bits for the memory columns : Fanin 1, 2, 4, 16
total : 54 relays per bitslice instead of 62.
For 18 bitslices, the cost is already 18×54=972 relays... or 1/3 of my current stock. There is still a 1/8 ratio of relay count vs bit count, which is a good sign.
OK my permutation problem is still unsolved.
Damnit !
I got the columns wrong again !
the MUX is actually a normal MUX16 BUT the end goes to 2 relays' middlepoint. So the actual Fanin is 1, 2, 4, 8, 16 just like the normal MUX16 but with one more layer.
D'oh
20170330
I got it all wrong again !
The column drivers are not optimal in the above configuration : driving 16 pairs of columns requires a 15-relays MUX16, then 2×16relays to switch the columns to 0V. That's a 3N factor, with a total of 47 relays ! Plus, the timing and power draw is not good.
If we accept to duplicate the tree of the MUX16, there are only 32 relays (or 2N) with the switch to ground at the root of each tree. The fan-in has doubled, though, but it might help a bit (for the permutations, see later) Power draw is better as well.
(Yes I've drawn the storage cap in reverse polarity)
For a 256-words memory :
- 4 address bits for the memory line : Fanin 1, 2, 4, 8
- 4 address bits for the memory columns : Fanin 2, 4, 8, 16
16+32=48 relays, and not 38... 864 (total for 18 planes), density : 5 bits/relay
For a 512-words memory :
- 5 address bits for the memory line : Fanin 1, 2, 4, 8, 16
- 4 address bits for the memory columns : Fanin 2, 4, 8, 16
That's about 64 relays, 1152 for 18 planes, 8 bits per relay : this is more favourable...
But the initial problem still persists !
Each board has MUXes of 3, 4 and 5 bits wide addresses .
However the double tree of the columns makes me think of a heuristic to partition the domain easily : for the case of 18 planes, work the partition with 9 planes, but instead of replicating the partition somewhere else, dupliate it with a shift/interleave. This turns the fanin1 look like fanin2, fanin2 becomes fanin4 and fanin4 becomes fanin8, which somehow "disappears" because there is no need to group it.
In the above drawing, each column represents a pair of bitplanes. The 9 columns get expanded into 18 bitplanes.
The resulting permutations are easier and the case of 4 addresses with 18/2=9 positions is pretty easy because only 2 lines (fanin 2 and 4) put some pressure. The only dissatisfying case is one blue string with only a length of 6, which is barely a problem, compared to other configurations, such as the previous 3:3, that require 1 resistor per bitplane...
The fanout per color is pretty neat : red=8×8=64, green=8×8=64, blue=(8×8)-2=62, black=10×8=80
But even the 3-lines case can benefit from pairing/doubling, the new version saves many resistors now. There are however pairs of relays (2 red, 2 green and 2 blue each) that need special care.
The fanout is totally balanced : 42 relays to drive from each address signal.
The case of the 5 addresses is more complicated (tm).
First, the 2x trick works but we get three dangling strings of 4. We would need a second MUX32 to merge the two halves. The fanout gets LARGE too ! 15×8=120 relays to drive the black or the yellow signal...
The deal-killer is that the 5-bits address is considered for an expansion of the memory, from 256 to 512 words. The process of going from 4 to 5 is really too convoluted. It would be easier to have two 4-bits fanout trees and a 5th address bit to select the proper MUX16, but this adds an "alternate address bus" to the layout...
-
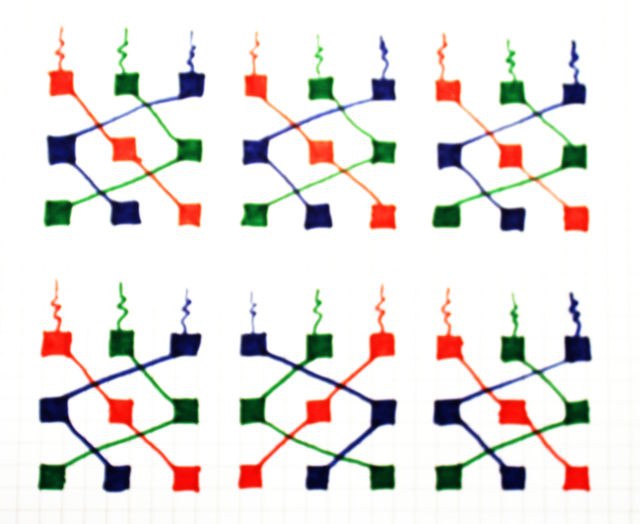
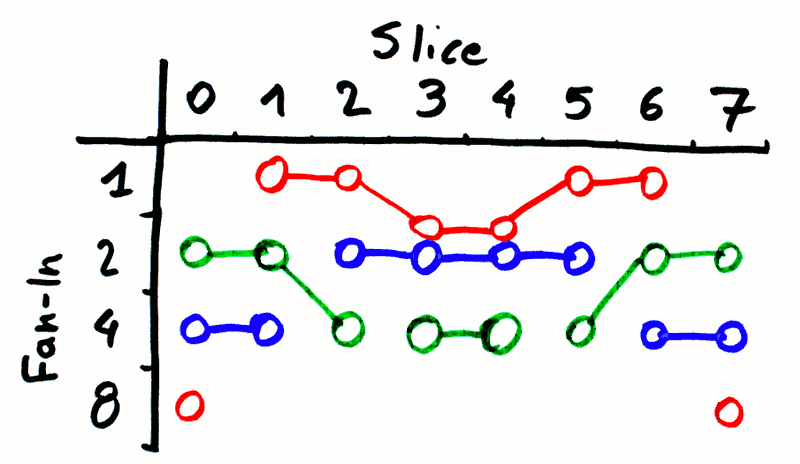
How to balance a fanout tree
12/16/2016 at 04:16 • 0 commentsI have a problem since the beginning. At least for the relay version, and probably others, the register set uses two MUX8 and one DeMUX8 per bit. This creates a fanout of 1 for the LSB of the address, but a fanout of 4 for the MSB (or vice versa). There is a very significant imbalance and the LSB drives 16 relays, while the MSB drives 64 relays !
The consequence is the increase in latency for reading operands (write decoding can overlap the execution). The LSB level can be switched quickly (FO=16) but the MSB level requires amplification stages, which delay the signal.
Ideally each address bit should drive one third of the MUX2. The numbers have decided otherwise : 16+32+64=112 (=16×7), there is no 3 as factor and 112/3=37.333... That's very inconvenient. But I have found that it's possible to approximate this goal with the help of some bit shuffling.
Let's remember two of the design constraints (at least for the relays) : all the bitslice are identical and a whole MUX level can't be split (on each board, or else this increases the routing complexity). As a consequence, an address bit has a "fan-in" of 1, 2 or 4. The trick is to send the 3 control signals to (globally) equal amounts of fan-in.
This means that each address bit will drive the MUX2 stage, the MUX4 stage and the MUX8 stage equally, or in other words : each bitslice receives a rotation of the address vector.
MUX2 MUX4 MUX8 0 0 1 2 1 1 2 0 2 2 0 1 3 0 1 2 4 1 2 0 5 2 0 1 6 0 1 2 7 1 2 0 8 2 0 1 9 0 1 2 10 1 2 0 11 2 0 1 12 0 1 2 13 1 2 0 14 2 0 1 15 0 1 2
There is obviously a problem with the last line, because 16 has no common divisor with 3.
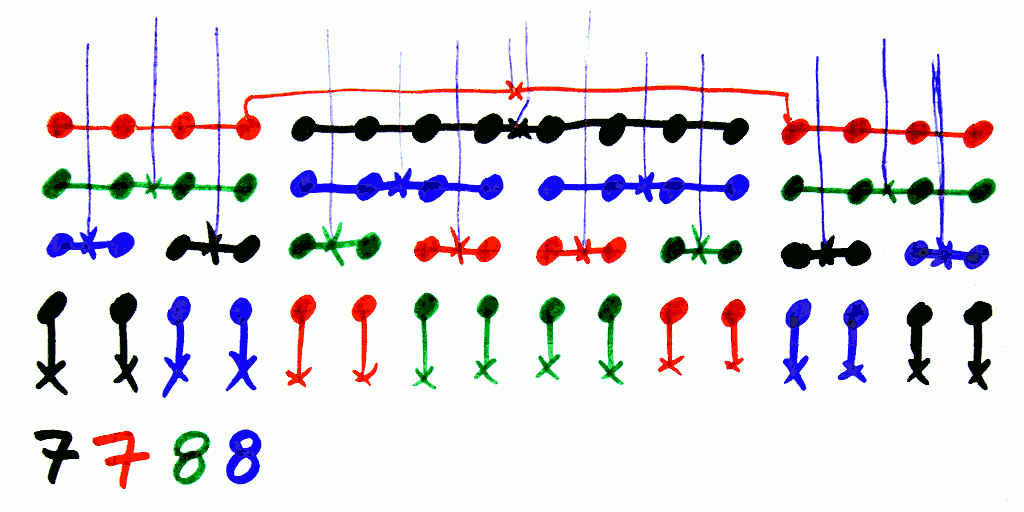
Another problem is specific to the relay implementation, using the CC-PBRL method: each "high voltage string" has 8 relays, two groups of four with the signal injection in the middle. This constrains the design even more but it almost matches with the current situation.
A "high voltage string" can drive one FI4, one FI2 and one FI1, this amounts to 7 relays. The 8th relay can be simulated by a resistor and bitslices become naturally grouped by 3 :
M2 M4 M8 bitslice%0 a b c bitslice%1 b c a bitslice%2 c a b a = b = c = 1 + 2 + 4 = 7 fan-inThis regular pattern helps design the drive logic and estimate the complexity.There would be 5 identical blocks of 3 slices, plus the last part. This requires a buffer with fanout of 5+1=6 (which can be done with a high-voltage string of 8). Since there is an identical buffer for every level, the latency is identical and all the bits arrive at the same time.
Yet this does not satisfy me because a string must have 8 relays, not 7. If the last relay is replaced with a resistor, 1/8th of the power gets wasted and this is not insignificant...
I found a much better circuit, which is explained with the simple diagram below:
![]()
Each group of 4 bitslices (wich evenly divides 16) has the same organisation (they can be mirored for convenience). Each bitslice has exactly one occurence of each color.
There are three full "long strings" of 8 Fan-In:
- 4-4
- 2-2-4
- 1-1-2-4
All these long strings have a "middle point" where the signal can be injected.
The remaining strings (1-1 and 2) can be assembled into a long string each, and it is just perfect (2-2-2-2 and 1-1-1-1-1-1-1-1) both in length and halvability.
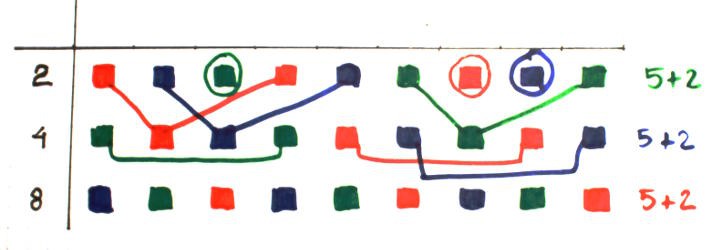
Conclusion : the balance is not perfect but still quite good:
- 4 strings of blue
- 5 strings of green
- 5 strings of red
It's certainly a bit more complicated than the initial fanout tree but no power is wasted in resistors. The fanout of 4 can be handled by 2 low-voltage CCPBRL (4 relays). I'll have to see if the CCPBRL can handle a fanout of 3, so the case of 5 can be handled with 2 and half low-level CCPBRL (5 relays and a resistor).
![]()
Finally, the layout of the bitslices is not changed : the coils of each level are wired in series (on each board) and the connector does not need to provide direct access to each and every relay with a pair of wires. This keeps the design compact.
The only requirement is to use the same pattern for the write MUX and the read MUXes, otherwise data written to one location will be read back on a different location...
For the (D)RAM address lines, a similar approach is possible. It only depends on the configuration.
- For 512 words, the rows have 3 bits (on the bitslice) and the columns have 6 bits (=64 wires on the backplane). The bitslices contain a MUX8 that uses the above pattern for the backplane.
- For 256 words, the address bits are split in half, 4 bits go to the bitslice in a different pattern. Unfortunately the highest level has a fan-in of 8, which is the maximum a long string can drive, and there are 16 of them (more than 8), requiring a 2-levels fanout tree instead of one...
A 4-deep tree is a different beast but should be possible. The total fan-in is 1+2+4+8=15, 15×16=240 relays. For an even fanout, 240/4 address bits=60 outputs per address bit, which is right under 8×8=64, so a single buffer level is required. The number has many small factors, which makes me think it's possible to make a nice, symmetrical fanout-tree.
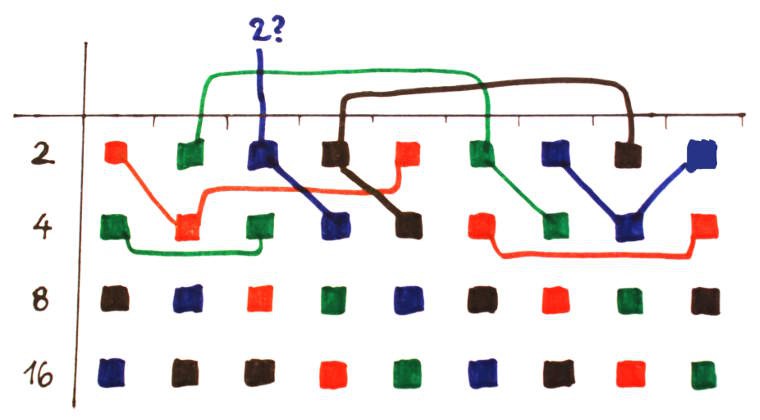
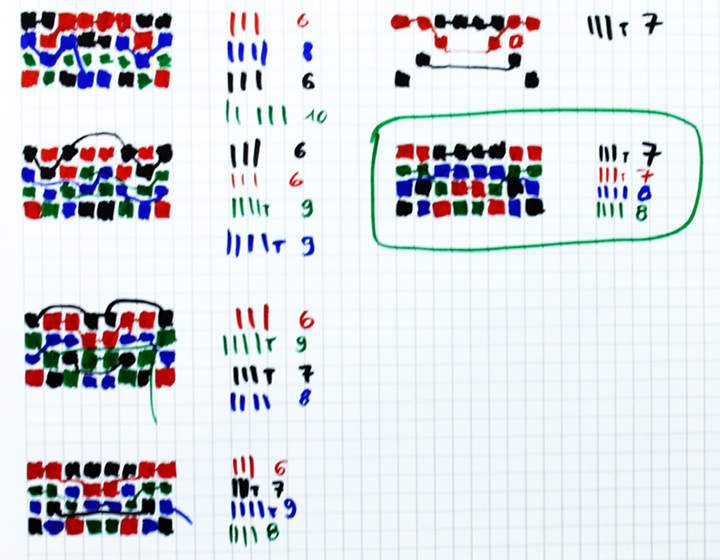
At first, I tried to play with different degrees of symmetry because I calculated that there had to be 15 strings for one half of the 16 slices.
Total fan-in: 15×16=240, 240/2=120, 120/4 address bits = 30
But 30 is not a multiple of 32, so the bits are split as 32-32-32-24 (or 4-4-4-3 strings of 8 each). The groups of 4 are inherently symmetrical but the group of 3 is a symmetry axis so I started avaluating all the possible arrangements (3) for 3 strings of 8:
![]()
Of those combinations, only one is viable : the red one touches the fanin8 signal (twice) while the others don't. It's a good starting point because the others would force the 3 other "colors" to access the FI8 input twice. Then I played with the combinations, using the red pattern as a basis.
![]()
I used a few heuristics but after the 4th attempts (bottom of left column), it appeared that the initial estimate did not work. The guidance of having one group of 6 strings "pushes" the other groups into having more strings than 8.
I relaxed the initial constraint to 7 strings (that's 3 and a half strings for 8 slices) and after a failed attempt, found one solution (in the green box). Expansion is easy with a simple duplication of the neighbours :-)
![]()
To me, it's quite beautiful and instead of having 8-8-8-6, we have a more balanced 8-8-7-7 (so only a couple resistors will waste energy).
Actually, the remaining fanout can be used for the parity DRAM bitplane.
Question : how does one handle a 17-wide fanout tree with 5 address bits ?...
-
Project split
12/04/2016 at 00:00 • 0 commentsThis project was meant to be an exploration of a design space and examination of a ruleset, not about a specific implementation.
I decided to split the project and continue the relay implementation as #YGREC16 - YG's 16bits Relay Electric Computer while I discuss here about higher-level considerations and features which will be common to other designs (such as #F-CPU and #YASEP Yet Another Small Embedded Processor )
-
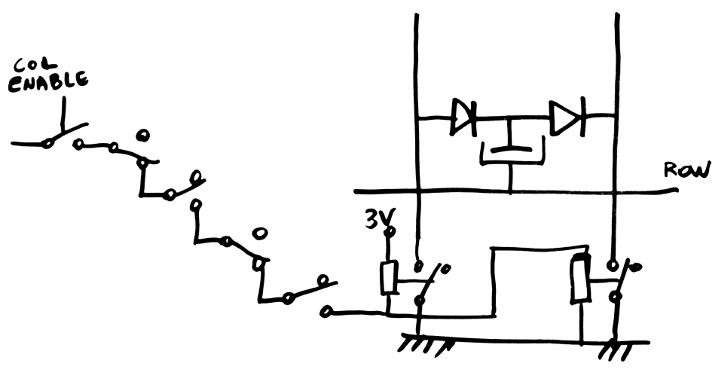
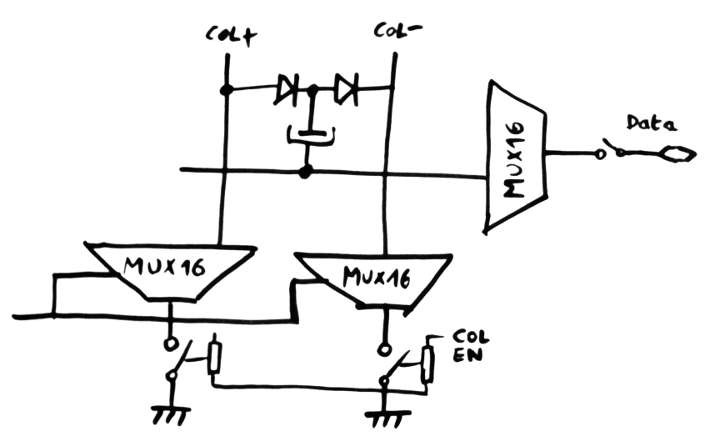
DRAM boards
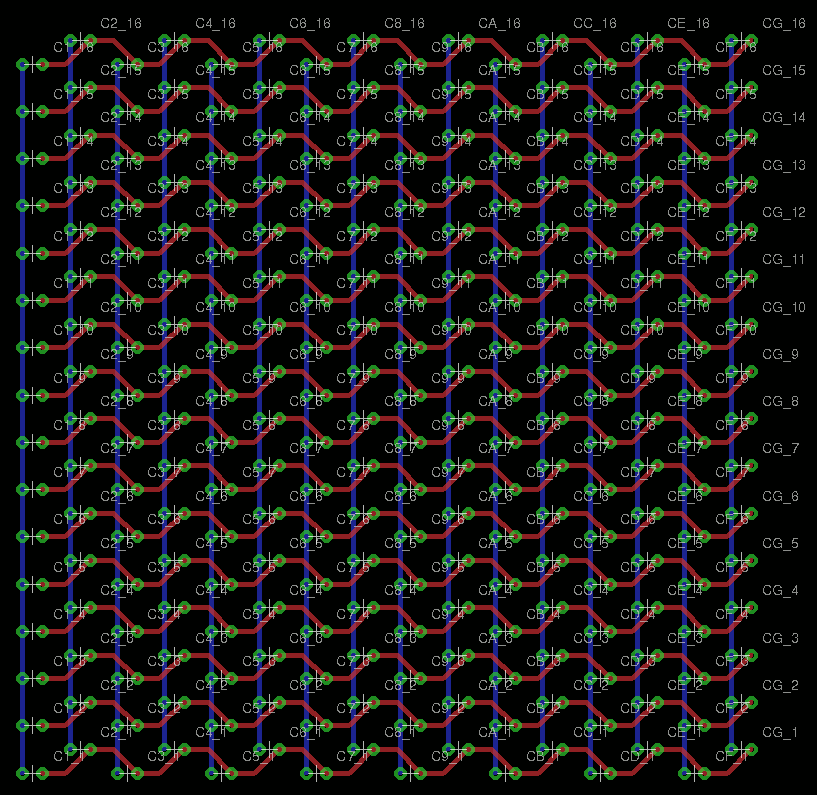
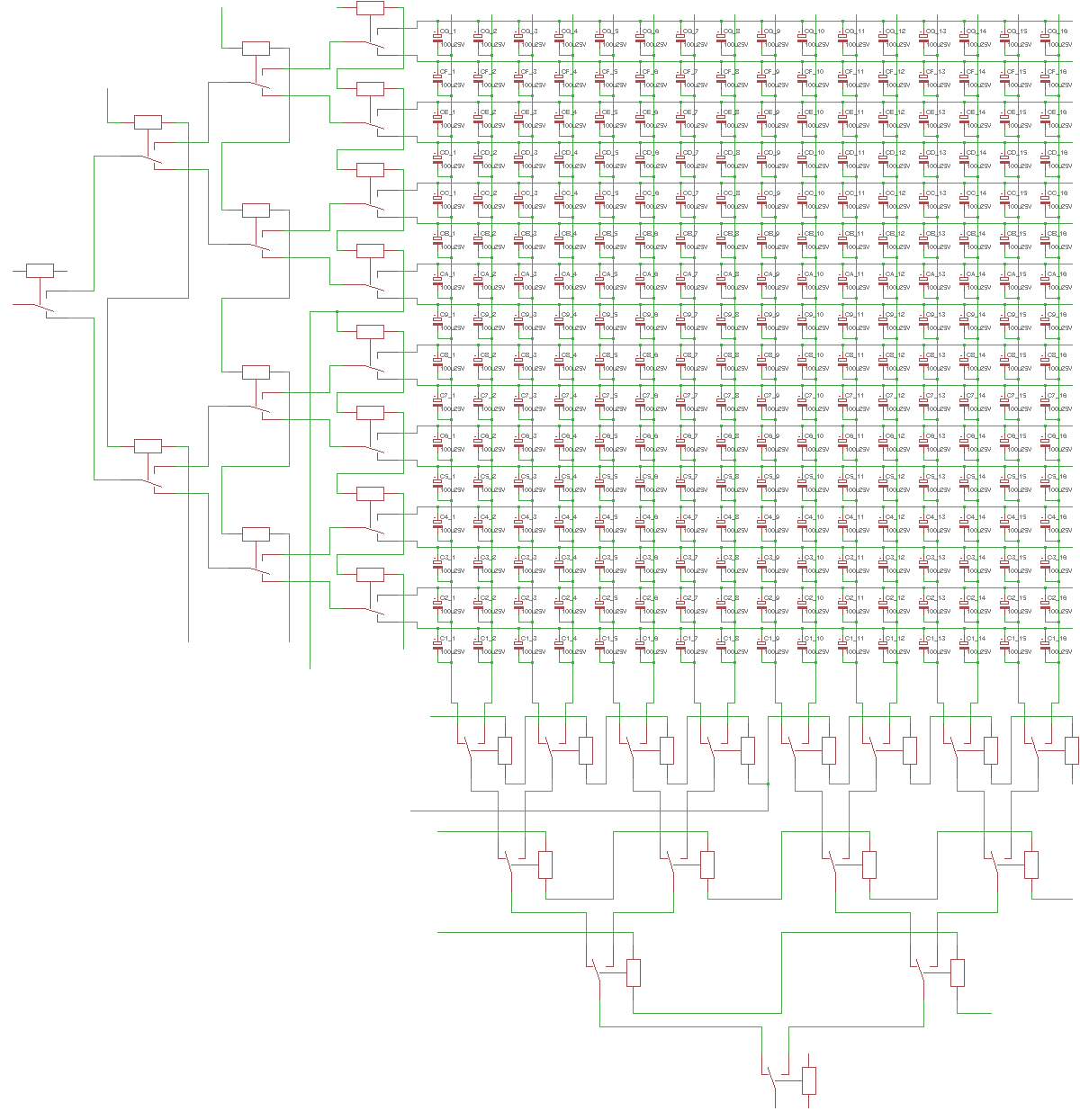
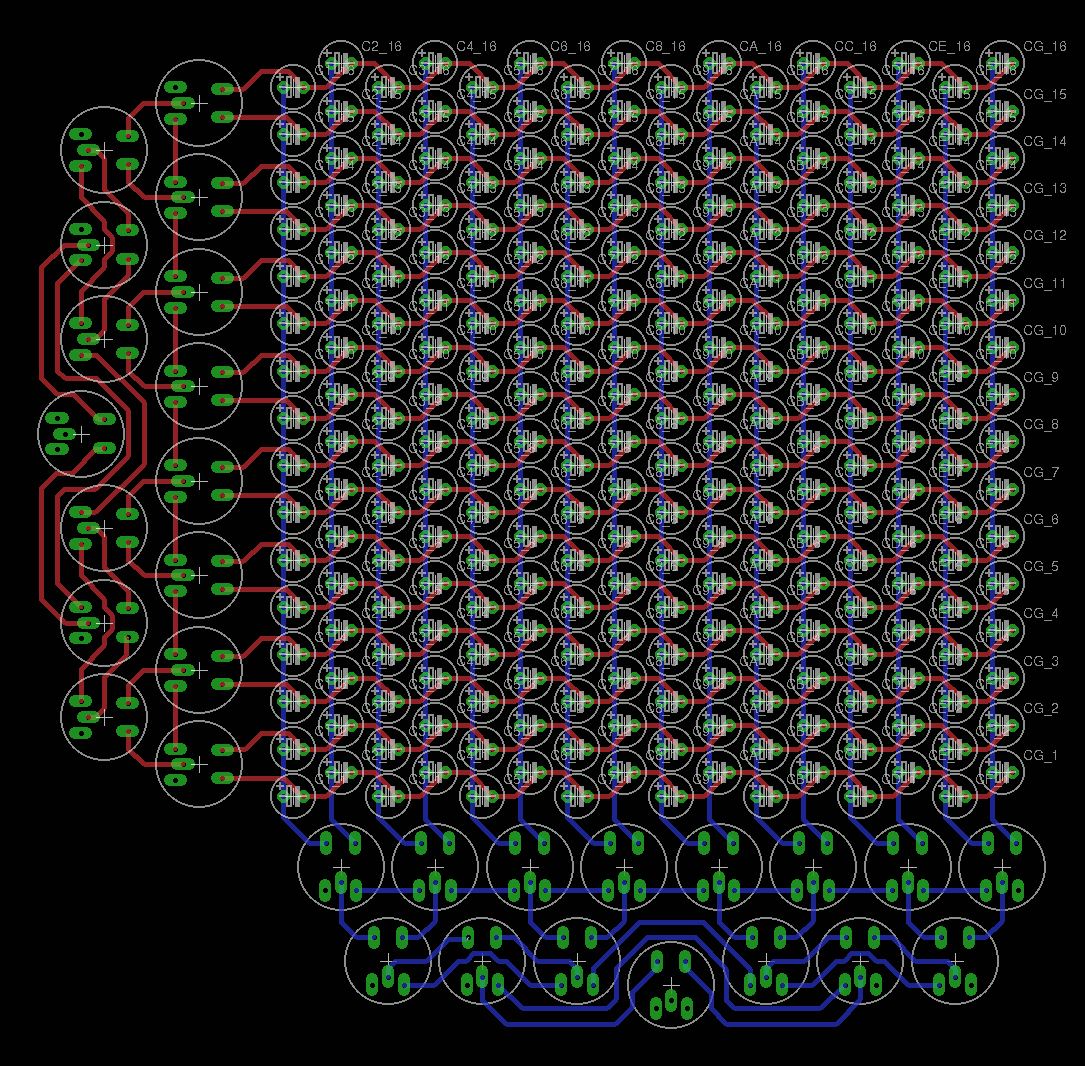
12/01/2016 at 19:48 • 0 commentsI have settled with a 16×16 capacitor array module, which I routed (with great pain) with Eagle:
![]()
With such a module, the design is more flexible so I can implement as much RAM as I need or want. I can swap modules if one is found defective. I can build as many bitplanes as required, for example for the 17th bit for parity.
The above layout uses 6mm diameter capacitor, though I also have 5mm in stock, at least only one board model is manufactured.
For the driving circuits, the best I could come up is a 256-words array. Each bitplane needs their set of relays (I tried otherwise and failed, or else I'd need tons of diodes and stuff, which makes the system more complex and probably delicate).
Each bitplane then has 15 relays for the X MUX16 and 15 for the Y DeMUX16. Plus the grounding relay, that's 31 relays per bitplane. With 17 bitplanes, that's 527 relays for 256 words... and 2.7A @12V=32W for the static power consumption.
![]()
![]()
Pretty simple, right ?
AMBAP: A Modest Bitslice Architecture Proposal
Trying to unify and simplify a minimal architecture for various implementation technologies...
 Yann Guidon / YGDES
Yann Guidon / YGDES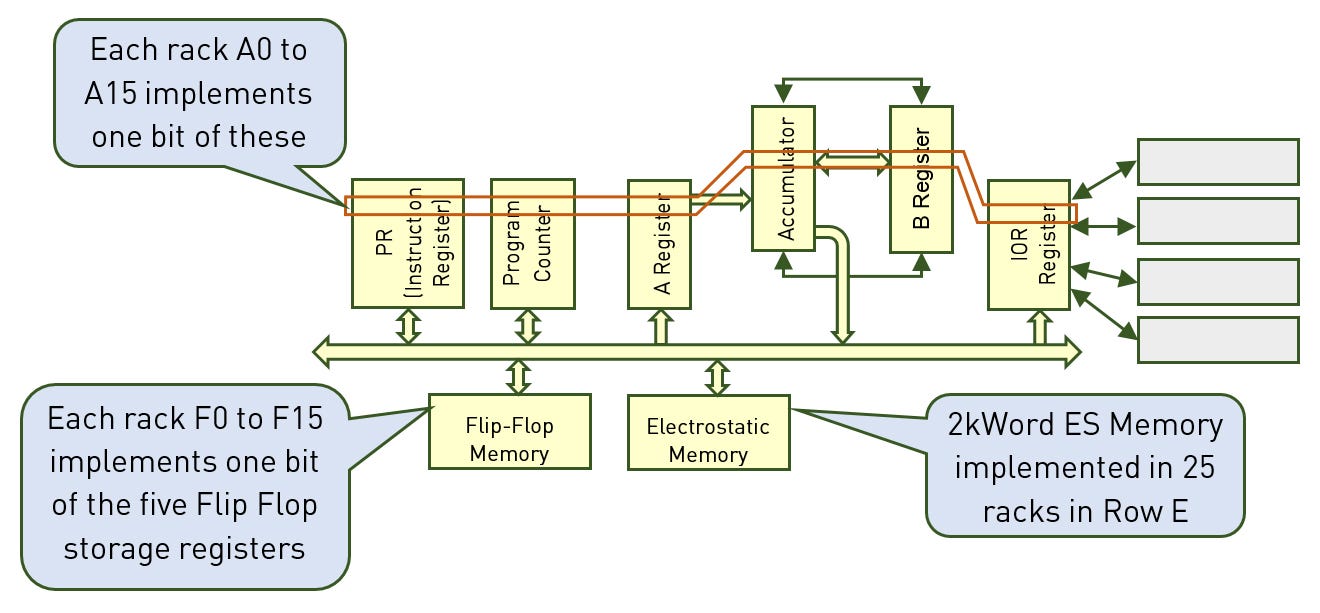


 There are:
There are: