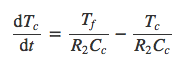MIMO kegerator

The next step in designing my "most complicated freezer closed loop control system" was to create a linear observer.

For my system model I have three temperatures I am currently measuring and I want to get rid of the temperature probe that measures the sidewall of the freezer!  Why, you might ask, would you go through this extra complicated step and decrease the reliability of your system by increasing complexity?

1.) Because I can.

2.) So I can learn.

Just to point this out:  One of my coworkers built a kegerator recently.  He purchased a ~$60 box that hangs on his wall that his freezer plugs into and has a temperature probe that he can stick either in a carboy or next to one of his kegs to control the temperature of the freezer.  It most likely uses some simple PID control algorithm.  I just want to put that out there so that everyone realizes the ridiculous level of complexity I am adding into what could be a very simple control system…

With that out of the way, the two textbooks I am referencing are:

Feedback Control Systems (Franklin, Powell), fourth edition

Control System Design, An introduction to State-Space Methods (Friedland), First Edition

I designed my linear observer using the example 7A in Friedland.  (See page 264 if interested.)  Chapter 7 in Franklin also helped as well.  I attached my math as a design file named “Linear Observer Design Sept 9 2018.pdf for those who are interested in taking a quick review.

I then proceeded back to Matlab and Simulink to see if my observer actually worked.

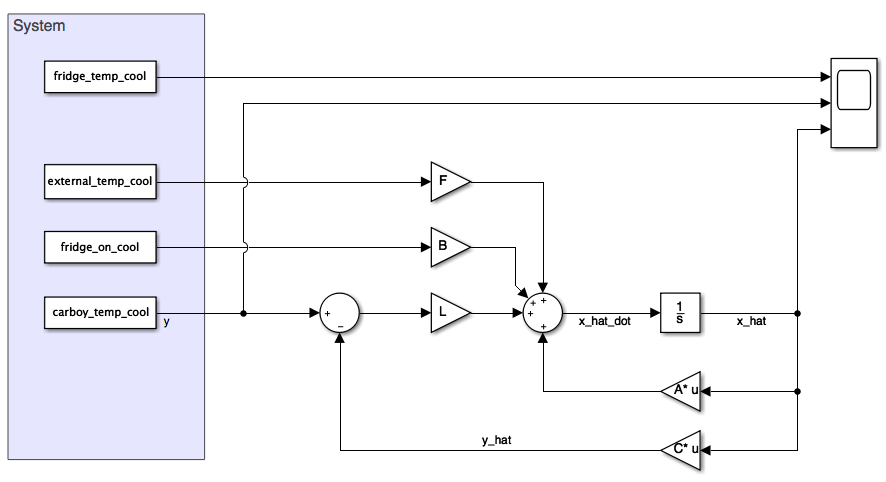
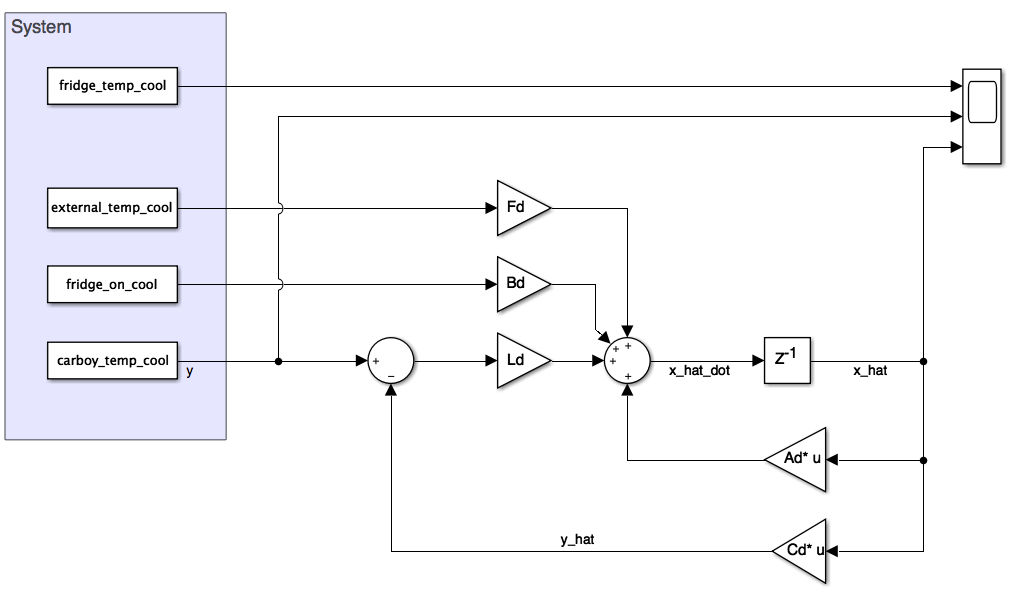
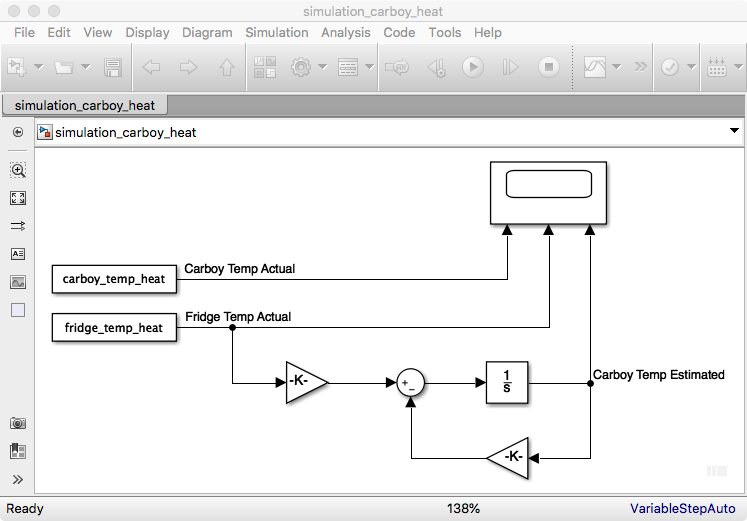
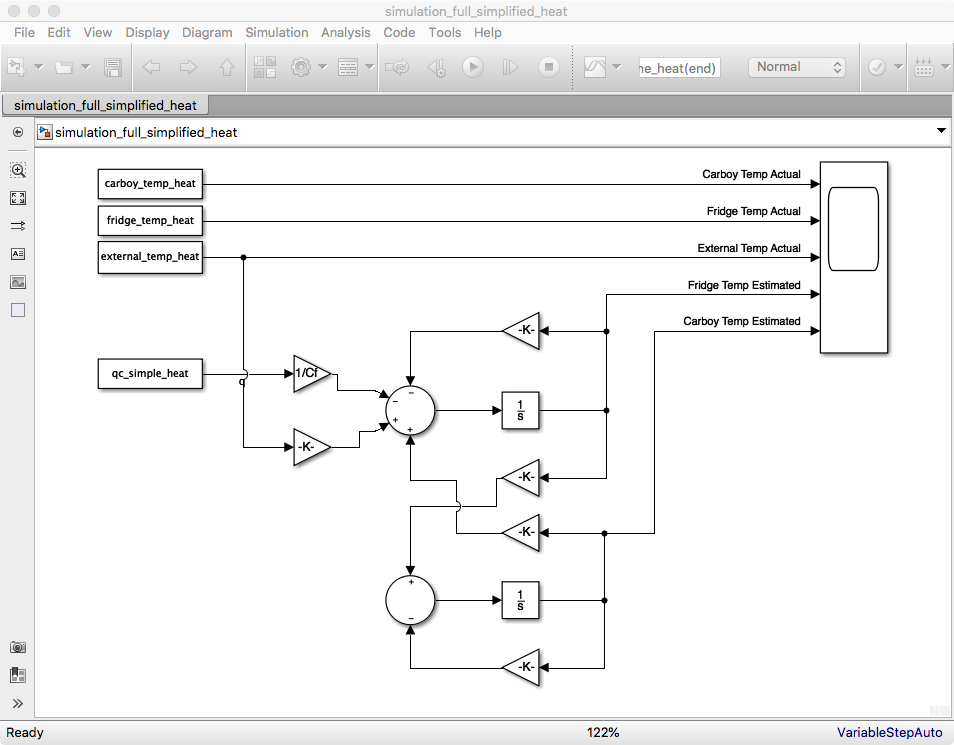
The first step was to validate operation in the continuous time domain.  I setup a quick model.  See below.

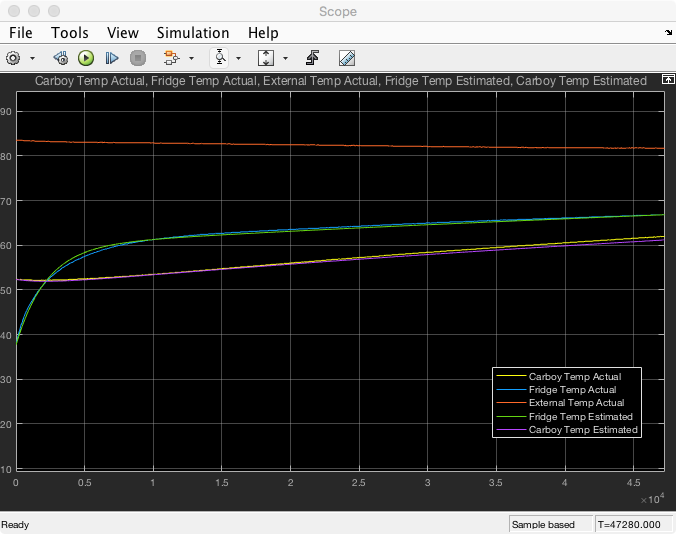
The simulation results tuned beautifully when I placed the two closed loop poles at 0.001 rad/s.

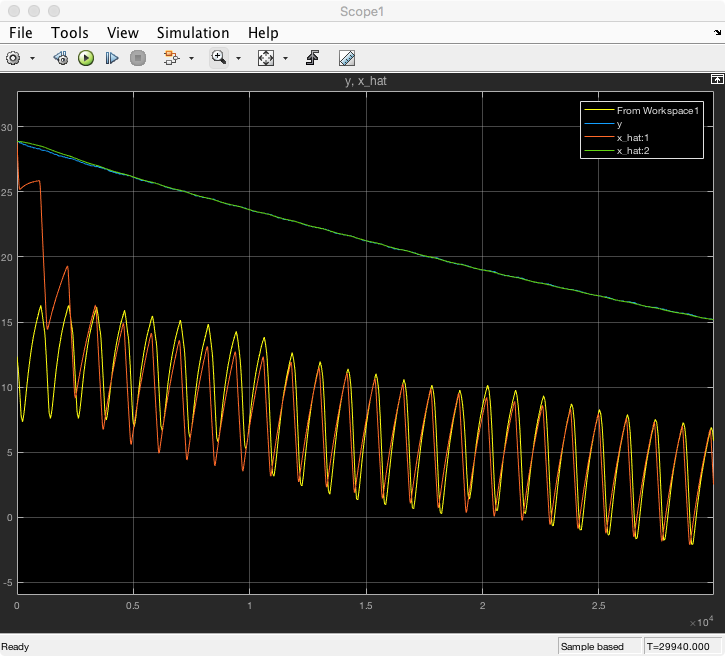
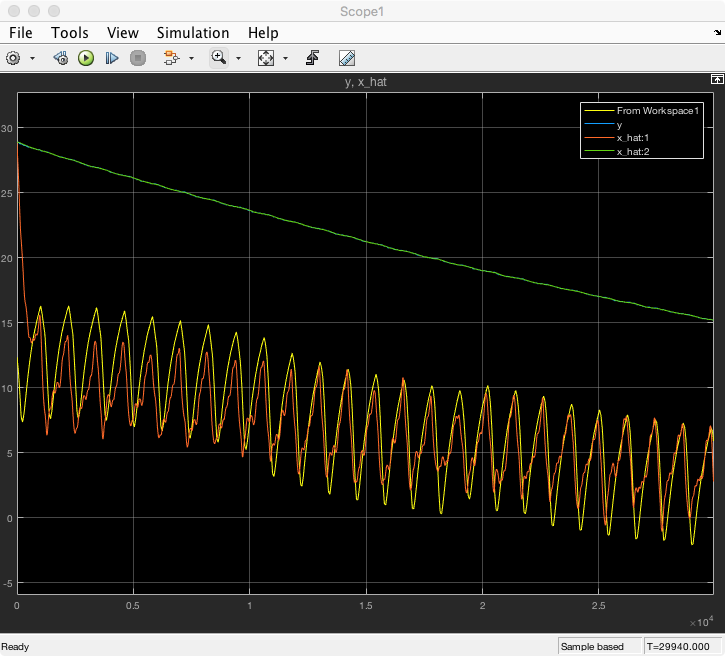
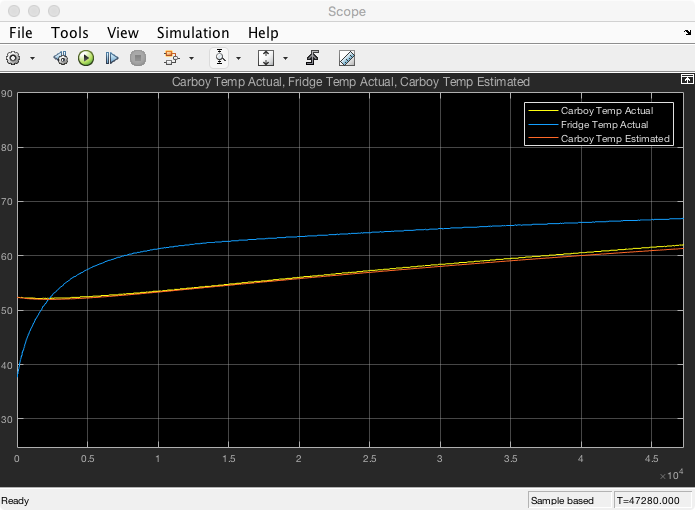
However as I moved the two poles further into the right half plane (i.e. faster response) the estimated value for the freezer wall would converge fast but started to have noticeable noise.  See below fora plot with poles at 0.005 rad/s.

Close up image below.

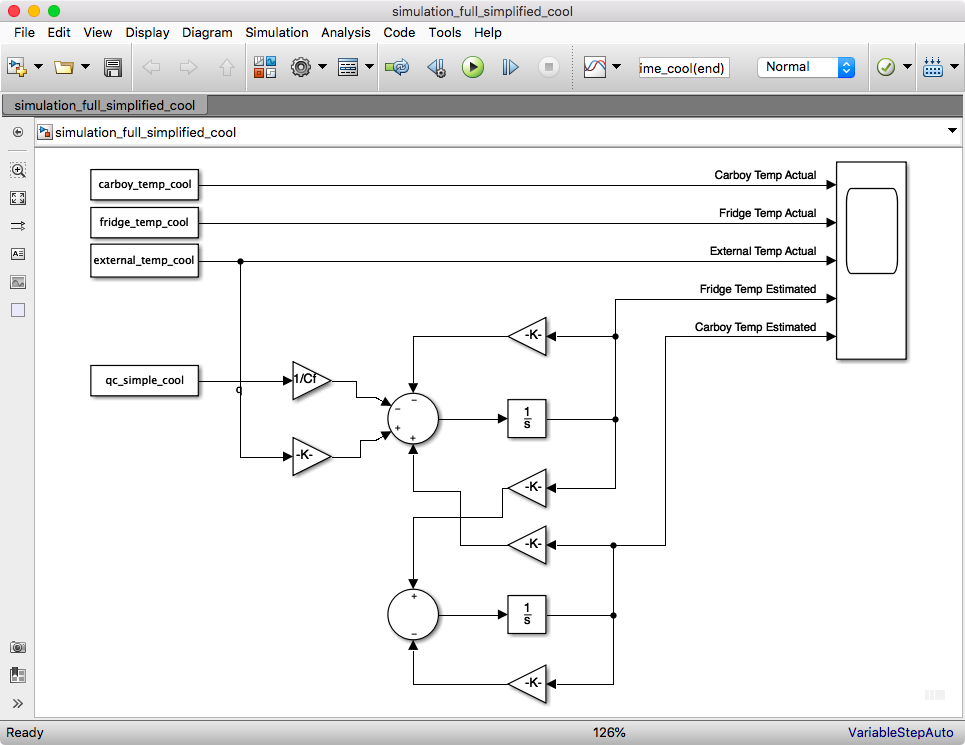
For initial system design I selected a pole at 0.001 rad/s.  I then converted by continuous time model into the digital domain.  I selected a sampling time of 1 second.  Matlab has a nice “c2d” function that I avoided.  I ended up quickly coding the conversion algorithm documented in chapter 8 (pg. 676) in Franklin and using c2d to check my work.  I then setup a new simulink model to validate that I didn’t mess anything up.  The simulink model is below.  It gave exactly the same results as the continuous time model.

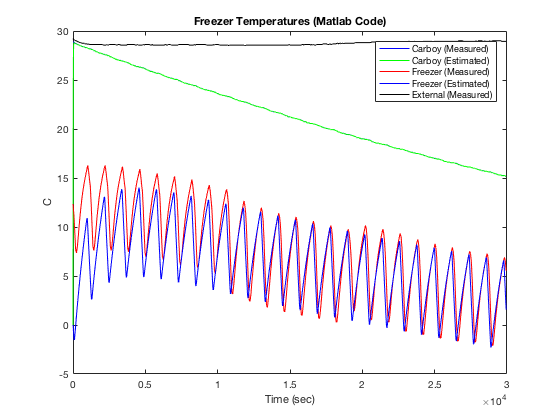
I then wrote the code for the state space algorithm in Matlab.  I did this so that I could quickly plot the results of the coded algorithm prior to coding them into the teensy controller.  I am glad I did as I quickly caught some typo errors that would have had me scratching my head.  As you will also notice it takes approximately 30 to 60 minutes for the freezer wall temperature estimate to converge to the measured value.  This is a LOT of time between troubleshooting.  Code is below for those interested.

% ----- Digital Code Verification -----
t = 0:Ts:time_cool(end);
Te = my_interp(external_temp_cool,t);
Tc = my_interp(carboy_temp_cool,t);
Tf = my_interp(fridge_temp_cool,t);
fridge_on = my_interp(fridge_on_cool,t);

Tc_e = zeros(size(t));
Tf_e = zeros(size(t));
%Tc_e(1) = Te(1);
%Tf_e(1) = Te(1);

for loop = 1:(length(t)-1)
    [Tf_e(loop+1), Tc_e(loop+1)] = observer_algorithm(Ad,Bd,Fd,Ld,Tf_e(loop),Tc_e(loop),Tc(loop+1),fridge_on(loop+1),Te(loop+1));
end

plot(t,Tc,'b');
hold on
plot(t,Tc_e,'g');
plot(t,Tf,'r');
plot(t,Tf_e,'b');
plot(t,Te,'k');
title('Freezer Temperatures (Matlab Code)');
legend('Carboy (Measured)','Carboy (Estimated)','Freezer (Measured)','Freezer (Estimated)','External (Measured)');
xlabel('Time (sec)');
ylabel('C');
hold off

The function "observer algorithm" is below.

function [Tf_e, Tc_e] = observer_algorithm(Ad, Bd, Fd, Ld, Tf_e_old, Tc_e_old, Tc, fridge_on, Te)
    a_11 = Ad(1,1); % A Matrix          0.9938
    a_12 = Ad(1,2); %                   0.0044
    a_21 = Ad(2,1); %                   0.0003067
    a_22 = Ad(2,2); %                   0.9997
    b = Bd(1);      % B Matrix          -0.4272
    f = Fd(1);      % F Matrix          0.0018
    l_Tf = Ld(2);   % Gain Matrix       0.0094
    l_Tc = Ld(1);   % Gain Matrix       0.6245

    error = Tc - Tc_e_old;
    
    Tf_e = Te*f + b*fridge_on + l_Tf*error + Tf_e_old*a_11 + Tc_e_old*a_12;
    Tc_e = l_Tc*error + Tf_e_old*a_21 + Tc_e_old*a_22; 
end

I posted the code because originally when I started designing controller algorithms in my spare time (yes, this is my hobby!) I had no idea on how to actually write the code for a digital controller.  It took me several weekends of staring at text books before it "clicked".  I wanted to share above as going from block diagrams you see in textbooks to the actual code to implement the algorithm is NOT obvious.  Or at least it wasn't to me.  

The next step was to implement the linear observer in the teensy.  I quickly found out that 1 sample a second for my interrupt was optimistic!  I currently have the teensy, reading the digital temperature sensors, computing the weight of the scale, performing calculations for the linear observer and then printing all the changing variables out over serial to the Raspberry Pi during each interrupt function.  This takes anywhere up to 2-3 seconds.  The two slowest parts of the interrupt are reading the digital temperature sensors and the serial communication to the Pi.  It is very easy to optimize this code.  Realistically an interrupt should NOT be used for performing serial communication however I previously had the interrupt running every 60 seconds when I was recording data to model the system and there was plenty of time for serial communication.

To keep the project moving I elected to change the sampling period to 10 seconds.  This is still wildly fast for the speeds at which the system dynamics in my freezer should be changing and allows me to send all the outputs from the calculations of the observer (and soon to come control algorithm) to the Pi so that I can troubleshoot the algorithms.

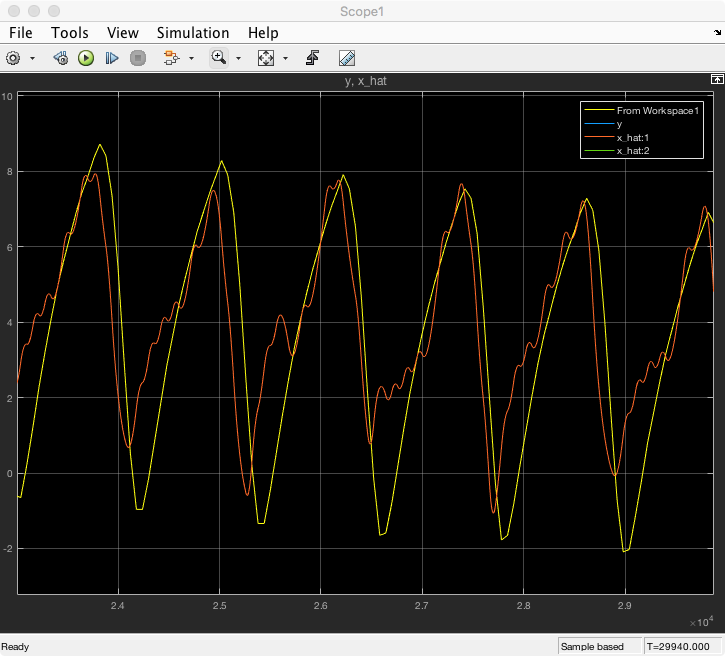
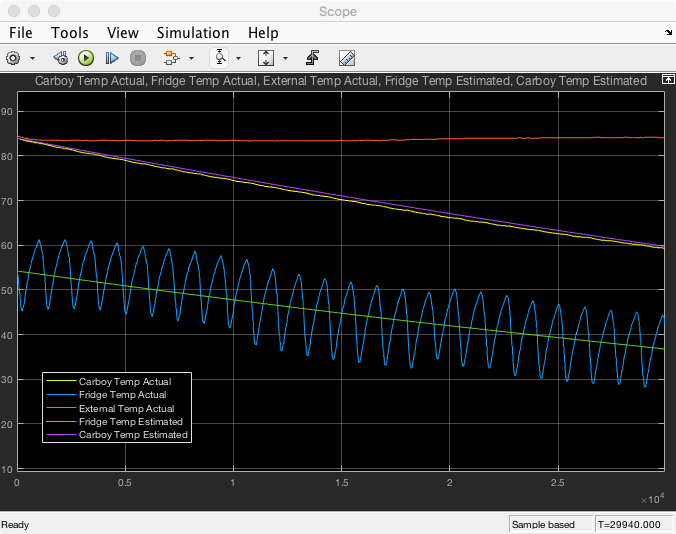
Based on the output of the linear observer results in Matlab code (not simulink) I increased the system poles to 0.005 rad/s.  I believe the reason that Simulink is having issues at 0.005 rad/s is that the signals I am using to validate the observer were sampled at a 60 second interval.  To increase the resolution for the simulink algorithms there is interpolation occurring that creates noise that is throwing off the simulation.  See below for the output from the Matlab code with poles at 0.005 rad/s.

Also interesting is that the Matlab code implementing my linear observer shows the linear observer goes unstable if I increase the closed loop observer poles much beyond 0.005 rad/s.  I believe this is due to the fact that I am only sampling every 10 seconds.  The closed loop bandwidth of 0.005 rad/s is ~0.0008 Hz.  This is about ~100 times slower than my sampling rate.  As my poles move right I am getting close to that magic point where the digital sampling rate is less than 20 times the closed loop bandwidth (i.e. 0.005 Hz).  At this point all bets are off and the system can be unstable simply because you are not sampling fast enough to approximate continuous control anymore.  Also there is noise in the sampling due to the digitization of the temperature samples.  While I know this noise is present I haven’t tried to really come to grips with how sensor noise is impacting my algorithm.  It could be impacting me more than I am aware.

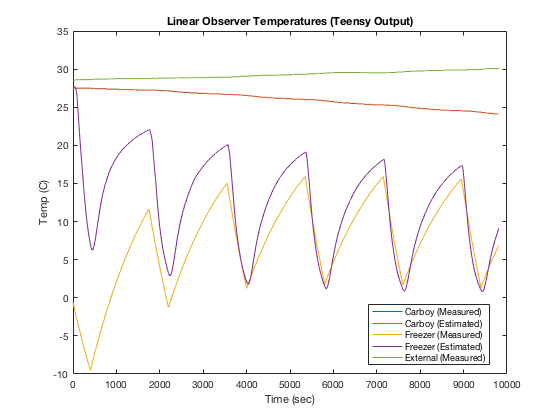
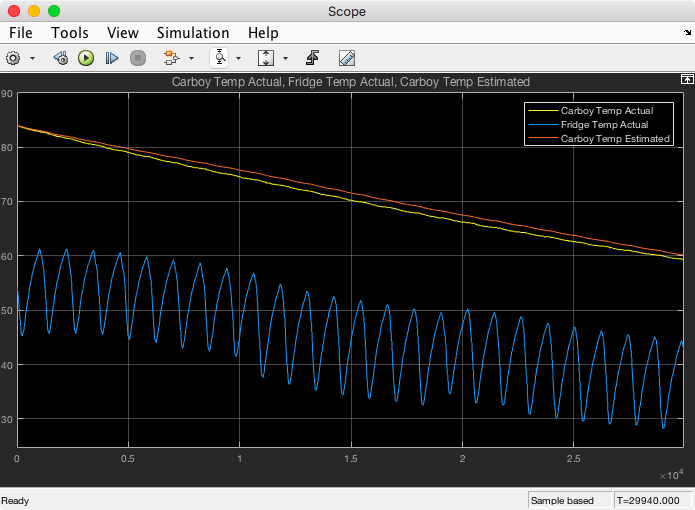
Anyway, it works!  See below for a plot of my estimator converging with the measured freezer temperature.  This is a plot of the output directly from the teensy.  (Matlab was only used to read in the values saved by the Raspberry Pi and plot the results.)  The estimate for the Carboy temperature converges very quickly.  The estimate for the freezer temperature, in this case, took about an hour.  Each cycle, where it cools and then warms is about 30 minutes.  The freezer is on for 25% of the 30 minutes. 

Stay tuned.  Next is closing the loop on controlling the freezer.  Whoo hoo!  :-)

With the freezer in the garage and the control system operating I started the next phase of the project:  system modeling.

I filled the carboy with 26.9 kg of tap water.  I then placed a temperature probe in the thermowell within the carboy, a temperature probe on the wall of the freezer and left a temperature probe out external to the freezer.

I then recorded four data files: Twice with the freezer cooling the carboy and twice allowing the carboy to warm up. 

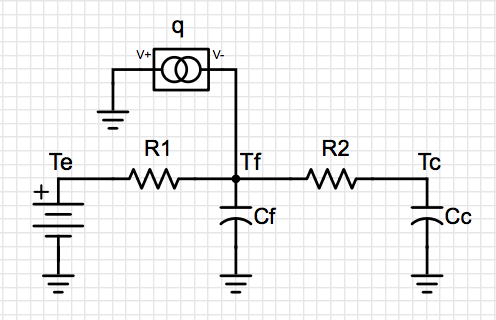
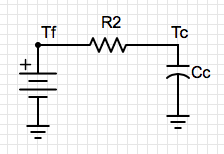
The model that I developed for the system is below.  It is an “electrical equivalent” model representing heat transfer between the ambient environment, the freezer and the carboy.  (Note the funny symbol for q is a current source pointed away from Tf to ground.)

Cc is the heat capacity of water in the carboy.

Cf is the heat capacity of the freezer.

q is the heat collected by the freezer.

R1 is the thermal resistance between the freezer and the ambient external environment.

R2 is the thermal resistance between the freezer and the carboy.

Te is the ambient external temperature.

Tf is the temperature of the freezer wall (measured from the inside of the freezer).

Tc is the internal temperature of the carboy.

The differential equations for the model are below.

By measuring Tc, Tf and Te I was able to calculate Cc, Cf, q, R1 and R2.  (I used Matlab and Simulink to run the simulations (version r2017b).  I am more than happy to upload the files for others to use if interested.  Matlab now offers a "hobby" edition of the matlab software for about $45.  Add on modules such as simulink are an additional $45.  I think they have been watching everyone migrate to Python.)

First I simulated the carboy temperature using the freezer wall temperature I measured.  This let me simplify my model to only R2 and Cc.  I assumed a Cc of ~50000 J/C using a specific heat of 4.18 kJ/(kg C).  I was then able to tune R2 so that when simulating Tc using Tf, R2 and Cc my simulated Tc match the measured Tc.  The simplified model is below.

Cc = 50000

R2 = 0.65

The simulation results and images of my simulink models are below.

As you can see the simulated Tc matches the actual measured Tc very closely.  The time axes is in seconds.

I then setup a simulink model for the larger system with Te and q as the inputs.  I then tuned the values for R1, Cf and q to align my simulation with my the measured Tc and Tf.  Results from the simulation are below.

R1 = 1.6

Cf = 5000

q = 156*pwm_percentage

It works!  It is very exciting again!  I finished all this work over the weekend and then did a little dance around the table.  I also noticed that my wife is very impressed with milestones in my projects.  She usually celebrates with some eye rolls and “that is vey nice honey” statements.  I take that as high praise indeed!

Next time update I should be able to provide feedback on development of my state space closed loop control algorithm!  (Also very exciting!)

I have successfully moved my project to the garage!  And it works. 

I wrote software for the Raspberry Pi to log temperatures and status from the teensy uC.  I have uploaded my current revisions of Teensy and the Python code I am using the Raspberry Pi.  The teensy is currently set up on an with a hard interrupt every 60 seconds and transmits temperatures, output of the scale at the bottom of the freezer and general status to the RPi for logging.  The teensy is currently programmed to turn on the freezer for five minutes out of every 20 minutes.  This is a 25% PWM cycle and is working like a charm.

I placed a carboy filled with water in the freezer and I am using the temperatures recorded to model the system.  In my next update I will add details on the mathematical model of the system and the values I have calculated.

I have been working on this project for the last month.  This first post is intended to document my progress.

I have purchased a small top open freezer and placed it in my garage.   (Make/Model:  Idylis 7.1 cu ft chest freezer)   I will be using this freezer to regulate the temperature of my keg/carboy.  I live in Texas so it is hot the majority of the time.  Initially I am planning on focusing my efforts on controlling the temperature of my freezer to cool my beer/carboy as needed.   The electronics I have designed will allow me to integrate a heating coil at a later date (i.e. in the winter!)

I purchased a small household scale and ripped out the electronics and soldered a cable to the wheatstone bridge scale elements.  (Make/Model:  Taylor 7042T)  The scale will sit in the bottom of the freezer and I will use it to calculate how much beer is in my keg as well as the specific gravity of my brew as it ferments.  To get the required resolution of the beer as it ferments I designed a unique analog circuit that implements a differential amplifier with a 12 bit digital to analog converter and 8 bit analog to digital converter to give a combined 20 bit resolution on the output of the scale.  I will update this page with information on my circuit design shortly.

I am using a Teensy as the micro controller to implement my control algorithm.  I have designed a custom interface board that allows my to plug my Teensy into the analog/digital circuitry to read my scale and four temperature sensors as well as be powered and communicate with a raspberry pi 3+.  The four temperature sensors each have a three wire digital interface.  (Make/Model:   Maxim Integrated, DS18B20+)

The Teensy will do the real time control of turning on and off the freezer to stabilize at an optimum temperature.  One of the temperature sensors will go into a thermowell that sticks down into my fermenting beer.  Another sensor will be integrated into an elastic strap that will go onto my keg once my beer is brewed.  Either of these temperature sensors will be the temperature input into my control system.  A third temperature sensor will measure the ambient temperature in my garage.  This will be the "disturbance" input.  The fourth temperature sensor will measure the ambient temperature in my project box that will be mounted on the wall and contain my electronics.  

Because I have two temperature inputs into my control system I will be able to teach myself how to implement a state space "MIMO" control algorithm.  (Super exciting!!!)  :-)  

The project box uses a din rail that I have mounted onto the metal plate in the back of a "Bussman" box.  On the din rail I have attached a 5V power supply (3A) that I am using to power my raspberry pi and Teensy micro controller and two 5V fans that circulate outside air through the project box.  I have two solid state relays that allow me to turn on and off 120V power.  (Make/Model:  Inkbird SSR-25DA)  One of the solid state relays will provide power to the freezer the other I am going to use to power a heating coil (when it gets cold outside).

That is about it for now:  The circuit to interface with the scale and temperature sensors has been designed and fabricated onto a OSHPark PCB.  The pcb has been integrated into the project box and connected to my Raspberry Pi.  I can read from all temperature sensors and the scale and turn on power to either output.

Now I need to program the thing:    My plan is to initially use the Raspberry Pi to provide a direct interface to the Teensy.  The Teensy will be programmed to do nothing other than read temperatures, the scale and turn on and off the freezer on command.  The Raspberry Pi is being programmed to act as a TCP/IP converter so that temperature/scale and freezer control can be controlled remotely from a copy of Matlab on my Mac.  I am going to use Matlab to model the thermal characteristics of the freezer and insulation so that I can get the model of my control system defined.  Once I have that I can then design my control algorithm and initially implement it in Matlab so that I can proof it and tweak it easily.

Now that progress to date and path forward have been documented I will see about uploading more pictures, schematics, and bill of material.