1. A little bit of theory

Between 291,000 and 646,000 people worldwide die from seasonal influenza-related respiratory illnesses each year. iF°EVE will change this. iF°EVE will be a life-saver like a defibrillator or a rescue helicopter. First we will take a look at the body core temperature classification:

ClassBody core temperature
Hypothermia< 35 °C
Normal36.5-37.5 °C
Fever> 38.3 °C
Hyperthermia> 40.0 °C
Hyperpyrexia> 41.5 °C


Easy to classify depending on the measured temperature only. Next we will take a look at the Naive Bayes classifiers that are commonly used in automatic medical diagnosis. There are many tutorials about the naive Bayes classifier out there, so I keep it short here.

Bayes' theorem:

\color{White} \large P \big(h|d)= \frac{P\big(d|h)\times P\big(h)}{P\big(d)} h: Hypothesis
d: Data
P(h): Probability of hypothesis h before seeing any data d
P(d|h): Probability of the data if the hypothesis h is true

The data evidence is given by

\color{White} \large P \big(d)= \sum_h P \big(d|h) \times P \big(h)where P(h|d) is the probability of hypothesis h after having seen the data d.

Generally we want the most probable hypothesis given training data. This is the maximum a posteriori hypothesis:

\color{White} \large h_{MAP}=arg~max_{h\in H} P \big(h|d)=arg~max_{h\in H} \frac{P \big(d|h)\times P\big(h)}{P\big(d)}

H: Hypothesis set or space

As the denominators P(d) are identical for all hypotheses, hMAP can be simplified:

\color{White} \large h_{MAP}=arg~max_{h\in H} P \big(d|h) \times P \big(h)If our data d has several attributes, the naïve Bayes assumption can be used. Attributes a that describe data instances are conditionally independent given the classification hypothesis:

\color{White} \large P \big(d|h)=P \big(a_{1},...,a_{T}|h) = \prod_t P \big(a_{t}|h) \color{White} \large h_{NB}=arg~max_{h\in H} P(h)\times \prod_t P \big(a_{t}|h)

Every human depending on the age catches a cold 3-15 times a year. Taking the average 9 times a year and assuming a world population of 7· 10^9, we have 63· 10^9 common cold cases a year. Around 5·10^6 people will get the flu per year. Now we can compute:

\color{White} \large P \big(Flu)= \frac{5 \times 10^{6}}{5 \times 10^{6}+63 \times 10^{9}} \approx 0.00008\color{White} \large P \big(Common~cold)= \frac{63 \times 10^{9}}{5 \times 10^{6}+63 \times 10^{9}} \approx0.99992This means only one of approx. 12500 patients with common cold/flu like symptoms has actually flu! Rests of the data are taken from here. The probability-look-up table for supervised learning looks then as follows:

ProbFluCommon cold
P(h)0.000080.99992
P(Fatigue|h)0.80.225
P(Fever|h)0.90.005
P(Chills|h)0.90.1
P(Sore throat|h)0.550.5
P(Cough|h)0.90.4
P(Headache|h)0.850.25
P(Muscle pain|h)0.6750.1
P(Sneezing|h)0.250.9

Therefore:

\color{White} \large h_{NB}=arg~ max_{h\in \big\{Common~cold,Flu\big\}} P(h)\times P(Fatigue|h) \times P(Fever|h) \times P(Chills|h) \times P(Sore~throat|h) \times P(Cough|h) \times P(Headache|h) \times P(Muscle~pain|h) \times P(Sneezing|h)Note: The probability that an event A is not occurring is given by

\color{White} \large P \big(\neg A\big) =1-P \big(A\big)Multiplying a lot of probabilities, which are between 0 and 1 by definition, can result in floating-point underflow. Since

\color{White} \large \log⁡(x\times y)=\log⁡(x)+\log⁡(y) it is better to perform all computations by summing logs of probabilities rather than multiplying probabilities. The class with highest final un-normalized log probability score is still the most probable:

\color{White} \large h_{NB}=arg~ max_{h\in H} \log \big(P(h)\big)+ \sum_t \log \big(P\big(a_{t}|h\big)\big)

2. Schematic

Below you will find the initial schematic (right click, view image to enlarge).

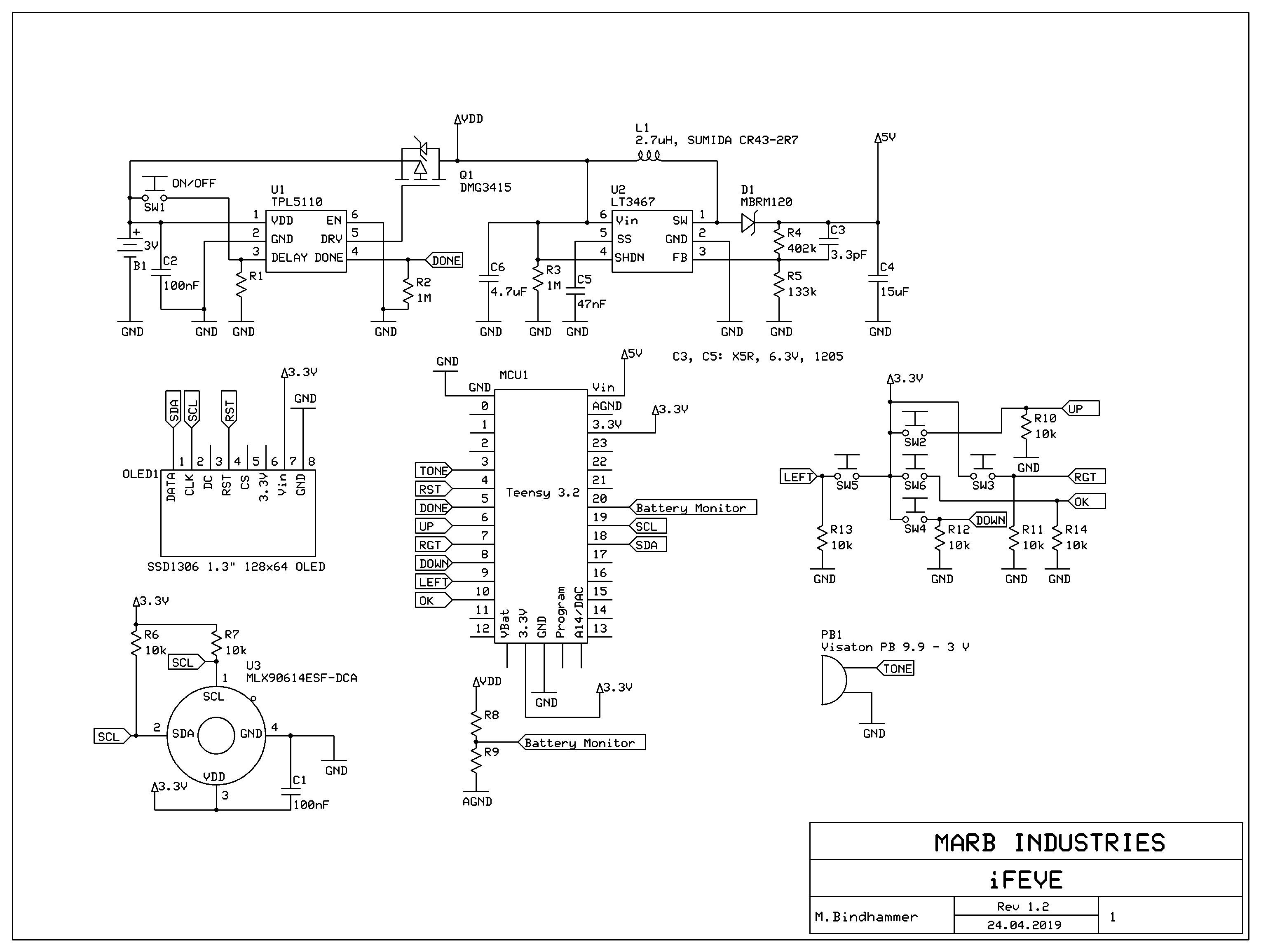
Body temperature measurement is done by the infrared thermometer MLX90614ESF-DCA. Temperature...

Read more »