Polyline Offset

Cross-Over Removal

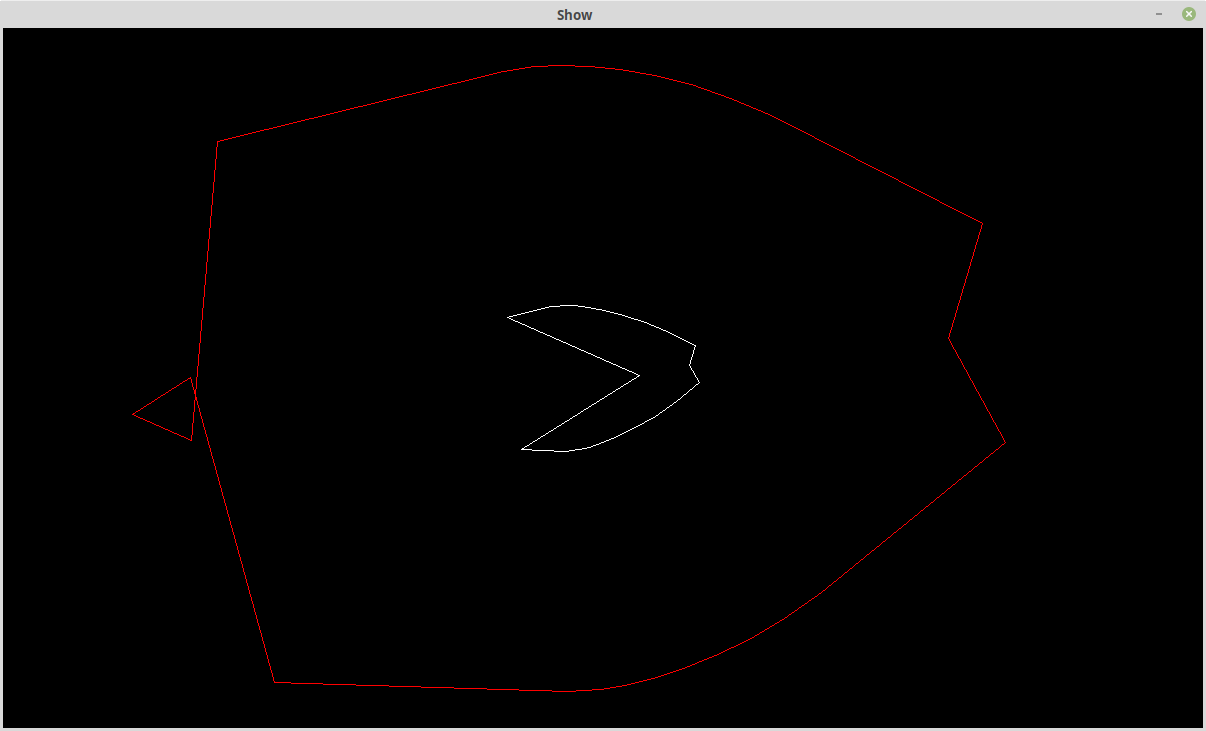
Added code to remove co-linear points (spikes) and cross-overs. While cross-over removal is rather ambiguous (i.e. which is the cross-over and which is the polyline?). Rather than get too "deep", I just decided to limit the search to only half of the polyline (by point count). Here is the expansion case, before:

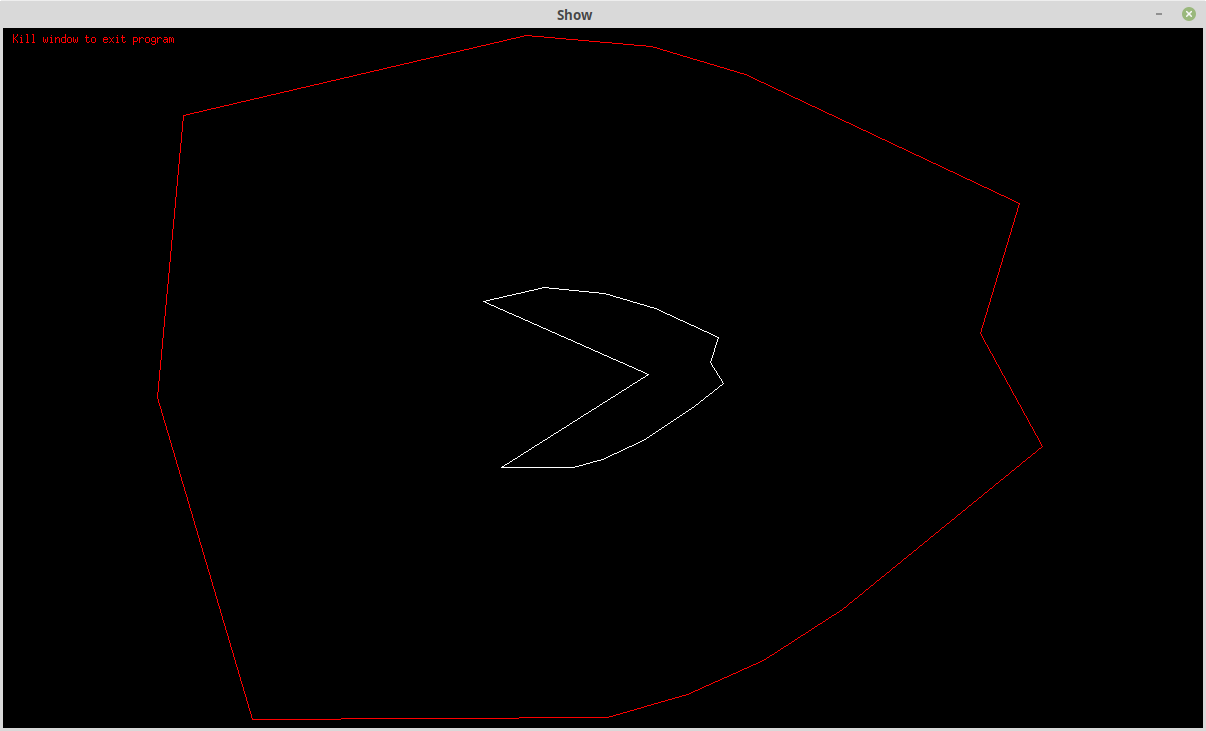
and after:

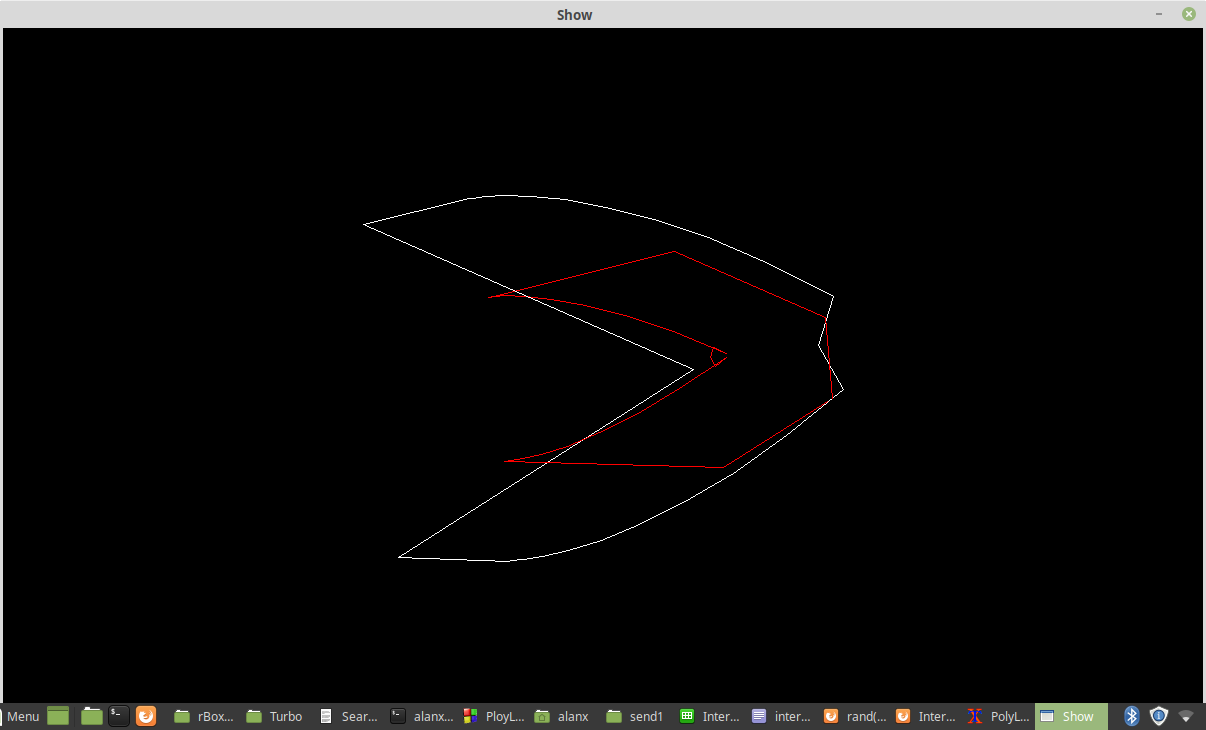
Here is the contractions case, before:

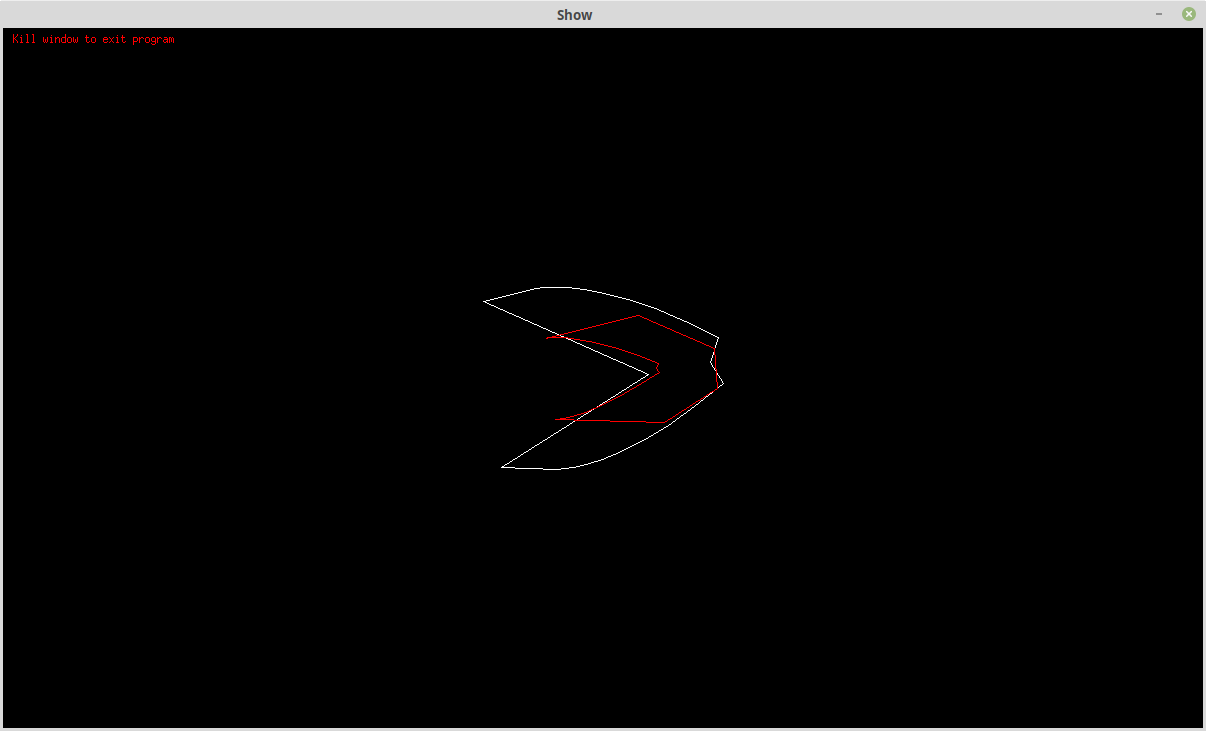
and after:

Well, that just about does it.

AlanX

Basic Code

The basic code is not too bad.

Here is my segment intersection routine:

int intersect(
  double px0,double py0,double px1,double py1,
  double px2,double py2,double px3,double py3,
  double *px,double *py) 
{
  double det,s,t;

  // Test if co-linear
  det=(px3-px2)*(py0-py1)-(px0-px1)*(py3-py2);
  if (fabs(det)>1e-12) {
    // Find ray intersection
    s=((px1-px0)*(py0-py2)-(py1-py0)*(px0-px2))/det;
    t=((px3-px2)*(py0-py2)-(py3-py2)*(px0-px2))/det;
    *px=px0+t*(px1-px0);
    *py=py0+t*(py1-py0);
    if ((s>=0.0)&&(s<=1.0)&&(t>=0.0)&&(t<=1.0)) {
      // Segment Intersection
      return 1;
    } else {
      // Ray Intersection
      return 2;
    }
  } else {
    // In my special case (for a polyline), I want the last point.
    *px=px3;
    *py=py3;
    return 0;
  }
}

The offset routine, considers the cases returned from the intersection routine:

int makeOffset(
  double x1,double y1,double xc,double yc,double x2,double y2,double Offset,
  double *xi1,double *yi1,double *xi2,double *yi2)
{
  double dx1,dy1,dl1,xo1,yo1,xc1,yc1;
  double dx2,dy2,dl2,xo2,yo2,xc2,yc2;
  double xi,yi;
  int Test;

  // Segment lengths
  dx1=xc-x1;
  dy1=yc-y1;
  dl1=sqrt(dx1*dx1+dy1*dy1);
  dx2=xc-x2;
  dy2=yc-y2;
  dl2=sqrt(dx2*dx2+dy2*dy2);
  if ((dl1>1e-12)&&(dl2>=1e-12)) {
    dx1=dx1/dl1*Offset;
    dy1=dy1/dl1*Offset;
    dx2=dx2/dl2*Offset;
    dy2=dy2/dl2*Offset;
    xo1=x1-dy1;
    yo1=y1+dx1;
    if (Offset>=0.0) {
      xc1=xc-dy1+dx1;
      yc1=yc+dx1+dy1;
      xc2=xc+dy2+dx2;
      yc2=yc-dx2+dy2;
    } else {
      xc1=xc-dy1-dx1;
      yc1=yc+dx1-dy1;
      xc2=xc+dy2-dx2;
      yc2=yc-dx2-dy2;
    }
    xo2=x2+dy2;
    yo2=y2-dx2;
    Test=intersect(xo1,yo1,xc1,yc1,xc2,yc2,xo2,yo2,&xi,&yi);
    if (Test==1) {
      // Segment Plus Offset Intercept
      *xi1=xi;
      *yi1=yi;
      *xi2=xi;
      *yi2=yi;
      return 1;
    } else if (Test==2) {
      double area=((y1-y2)*(xc-x2)-(yc-y2)*(x1-x2));
      if (((area<0)&&(Offset<0))||((area>0)&&(Offset>0))) {
        // External Ray Intercept (use truncated offsets)
        *xi1=xc1;
        *yi1=yc1;
        *xi2=xc2;
        *yi2=yc2;
        return 2;
      } else {
        // Internal Ray Intercept (use intercept)
        *xi1=xi;
        *yi1=yi;
        *xi2=xi;
        *yi2=yi;
        return 3;
      }
    } else {
      // Co-linear Intercept
      *xi1=xi;
      *yi1=yi;
      *xi2=xi;
      *yi2=yi;
      return 4;
    }
  }
  return 0;
}

One problem with the offset code is what to do with very short segments ?

My solution filter the polyline for:

• segments (points) that are nearly co-linear,
• segments that are very short.

  // Filter Points (Open Polyline)
  Test=true;
  while (Test) {
    Test=false;
    int count=0;
    for (i=0;i<=N;i++) {
      count++;
      if (count>=3) {
        double area=fabs((Y[i-1]-Y[i-2])*(X[i]-X[i-2])-(Y[i]-Y[i-2])*(X[i-1]-X[i-2]));
        double length=sqrt((Y[i]-Y[i-2])*(Y[i]-Y[i-2])+(X[i]-X[i-2])*(X[i]-X[i-2]));
        if ((length*fabs(Offset)>area*100)||(fabs(Offset)>length*10)) {
          D[i-1]=true;
          Test=true;
          count=1;
        }
      }
    }
    int j=0;
    for (i=0;i<=N;i++) {
      if (!D[i]) {
        X[j]=X[i];
        Y[j]=Y[i];
        D[j]=false;
        j++;
      }
    }
    N=j-1;
  }

Finally the make Polyline Offset code:

  // Polyline Offset
  x1=X[N-2];
  y1=Y[N-2];
  xc=X[N-1];
  yc=Y[N-1];
  x2=X[0];
  y2=Y[0];
  makeOffset(x1,y1,xc,yc,x2,y2,Offset,&xc1,&yc1,&xc0,&yc0);
  NT=0;
  XT[NT]=xc0;
  YT[NT]=yc0;
  NT++;
  for (i=0;i<N;i++) {
    i1=(i+N-1)%N;
    ic=(i+N)%N;
    i2=(i+N+1)%N;
    x1=X[i1];
    y1=Y[i1];
    xc=X[ic];
    yc=Y[ic];
    x2=X[i2];
    y2=Y[i2];

    ezx_line_2d(disp,width/2+(int)(scale*x1),height/2-(int)(scale*y1),width/2+(int)(scale*xc),height/2-(int)(scale*yc),&ezx_white,1);
    Test=makeOffset(x1,y1,xc,yc,x2,y2,Offset,&xc1,&yc1,&xc2,&yc2);
    if (Test==1) {
      // Normal Intercept
      ezx_line_2d(disp,width/2+(int)(scale*xc0),height/2-(int)(scale*yc0),width/2+(int)(scale*xc2),height/2-(int)(scale*yc2),&ezx_red,1);
      XT[NT]=xc2;
      YT[NT]=yc1;
      NT++;
    } else if (Test==2) {
      // Truncated Intercept
      ezx_line_2d(disp,width/2+(int)(scale*xc0),height/2-(int)(scale*yc0),width/2+(int)(scale*xc1),height/2-(int)(scale*yc1),&ezx_red,1);
      ezx_line_2d(disp,width/2+(int)(scale*xc1),height/2-(int)(scale*yc1),width/2+(int)(scale*xc2),height/2-(int)(scale*yc2),&ezx_red,1);
      XT[NT]=xc1;
      YT[NT]=yc1;
      NT++;
      XT[NT]=xc2;
      YT[NT]=yc2;
      NT++;
    } else if (Test==3) {
      // Ray Intercept
      ezx_line_2d(disp,width/2+(int)(scale*xc0),height/2-(int)(scale*yc0),width/2+(int)(scale*xc2),height/2-(int)(scale*yc2),&ezx_red,1);
      XT[NT]=xc2;
      YT[NT]=yc2;
      NT++;
    } else if (Test==4) {
      // Polyline Co-linear Intercept
      ezx_line_2d(disp,width/2+(int)(scale*xc0),height/2-(int)(scale*yc0),width/2+(int)(scale*xc2),height/2-(int)(scale*yc2),&ezx_red,1);
      XT[NT]=xc2;
      YT[NT]=yc2;
      NT++;
    } else {
      // General Colinear Intercept
      ezx_line_2d(disp,width/2+(int)(scale*xc0),height/2-(int)(scale*yc0),width/2+(int)(scale*xc2),height/2-(int)(scale*yc2),&ezx_red,1);
      XT[NT]=xc2;
      YT[NT]=yc2;
      NT++;
    }
    xc0=xc2;
    yc0=yc2;
  }

One problem with this code is that it uses the previous point. This can lead to an asymmetrical result.

Cross-Over Removal

Cross-over removal is the next challenge.

AlanX