Nixie Tube 170 V flyback DC-DC power converter

The capacitance added at the input and output of the converter will impact the voltage ripple.

Output capacitance

There are some different ways to choose the output capacitance. One approach is determine the voltage ripple of the converter, and solve for the capacitance needed to meet the ripple spec. From the circuit diagram in the details section, the capacitor discharges during the on state. Using the small ripple approximation that the current is about constant during this interval, the voltage ripple can be expressed as

Solving for C:

Nixie tubes don't need perfect DC, so a peak-to-peak ripple of 1 V is more than sufficient. Under the target load of 30 mA and the maximum duty cycle at 5 V input of .773, the required output capacitance is 66 nF.

Another way to pick output capacitance is by the desired load transient over/undershoot. When output current jumps, the output voltage briefly drops before the feedback loop returns things to regulation. How sharply the voltage undershoots is a function of both the output capacitance and the bandwidth of the feedback loop.

A crude way to estimate the load transient is to observe that below the crossover frequency, the feedback loop reduces the effective output impedance of the converter, and at high frequencies, the output impedance of the converter is also low because of the output capacitance. The converter's output impedance is likely at a maximum near the crossover frequency, and this can be used to estimate the magnitude of the load transient:

Skipping ahead to the results of the compensation section I'll talk about soon, I ended up picking 8 kHz as the crossover frequency. Let's say I want to keep the voltage undershoot to 1 V when the load goes from 50% to 100% (15 mA to 30 mA). The required output capacitance from this formula is 298 nF.

I ended up using the latter method and rounded this up to 2 x 220 nF capacitors with a 10 nF ceramic capacitor to handle very high frequency transients. The larger capacitors are film type for their low ESR/dissipation factor and high voltage ratings. In this capacitance, film capacitors are available using either PP or PET plastic. PP has superior dissipation factor, but I'm not sure it matters for this application, so I picked a package where I could try both.

Input capacitance

One way to size the input capacitance is to imagine the input capacitor alone supplies current to the inductor during the on-state, and gets recharged instantly when the switch turns off. How much capacitance would be needed to meet the desired ripple spec? The voltage ripple of a capacitor sourcing the average inductor current during the on period is:

I want the input voltage to drop no more than 1% or 50 mV. Using the maximum current and duty cycle conditions (Vg = 5 V, D = .773, IL = 1.4 A), then the required input capacitance is 62 µF. I rounded this up to 2 x 47 µF aluminum poly bulk capacitors. In addition, a few ceramic 10 µF or smaller caps will help reduce high frequency spikes.

Now that the controller chip has been chosen, there are a lot parts to pick based on datasheet requirements. Most of these choices are straightforward, but some, such as the choice of switching frequency, need some consideration of the limits of other parts choices, and the compensation components, which will require extensive theoretical development or some intuition coupled with experimental evaluation.

Converter design parameters

• Input voltage: 5 to 12 V
• Output voltage: 170 V
• Maximum output current: 30 mA

Switching frequency

The way I picked the switching frequency was to work backwards from the maximum inductor current ripple limit. The results in the details section rely on the idea that the average inductor current can be substituted for the time-varying result. If this assumption, called the small-ripple approximation, is no longer true, than more complicated mathematics must be applied, as is the case when the inductor current goes to zero during the switching cycle, and the converter is said to be operating in discontinuous conduction mode (DCM).

During the on-state of the switching cycle, the voltage applied from the input source ramps the current in the inductor. For an inductor, v = L (di/dt), so the slope of this ramp is v/L. The peak-to-peak ripple is this slope times the amount of time the switch is on and this voltage is applied:

Solving for the switching frequency (reciprocal of the period T):

The maximum duty cycle and current occur at the lowest input voltage (5 V). The computed duty cycle and inductor current are D=.773 and IL = 1.4 A. I'd like to keep the ripple to less than 40% of the average current, so plugging values in, the resulting switching frequency is 366 kHz. I rounded this to 350 kHz and used the timing resistor formula in the LM5155 datasheet to obtain a timing resistance of 62 kΩ.

Feedback resistors

The voltage reference on the LM5155 is an even 1 V, so I need to reduce the output voltage of 170 V to 1 V, preferably without burning much current since this converter is designed to supply 30 mA. As luck would have it, there is an E96 value combo that gives us an exact 1/170 resistor divider and draws less than 1 mA at 170 V: use a 1.69 MΩ & 10 kΩ divider.

Undervoltage lockout (UVLO)

The LM5155 has a feature to adjust the UVLO levels that shutdown the converter, with  configurable hysteresis. This isn't important for an evaluation board that will checked out on the bench, but I decided to set an on value of 4.75 V and off value of 4.6 V. The datasheet has a formula to set the resistor divider on the UVLO pin, which yields R1 (top) = 18.7 kΩ and R2 (bottom) = 8.66 kΩ - these are rounded to the closest E96 values.

Soft start

The soft start circuit in the LM5155 charges the voltage reference using a 10 µA current source into the attached external capacitor. Once the voltage on the SS pin hits 1 V, the internal voltage reference takes over, so the soft start time is determined by the time it takes to charge the capacitor to 1 V, so 10 nF gives a startup ramp time of 1 ms. I don't consider this critical for a evaluation board powered by a bench power supply, and some datasheet examples used 22 nF, so I picked this as a starting point.

Current sense network

This section relies on results from the theory of current programmed control that are not immediately obvious. An excellent reference on current programmed mode is chapter 12 of Fundamentals of Power Electronics by Erickson and Maksimović.

The LM5155 uses peak current control (also called current programmed mode) to set the duty cycle. This offers overcurrent protection and also improves the stability of the feedback loop. The inductor current is sensed by observing the voltage at a low-side shunt resistor. When the voltage level at the CS pin hits the controller's threshold, the MOSFET turns off for the rest of the switching cycle.

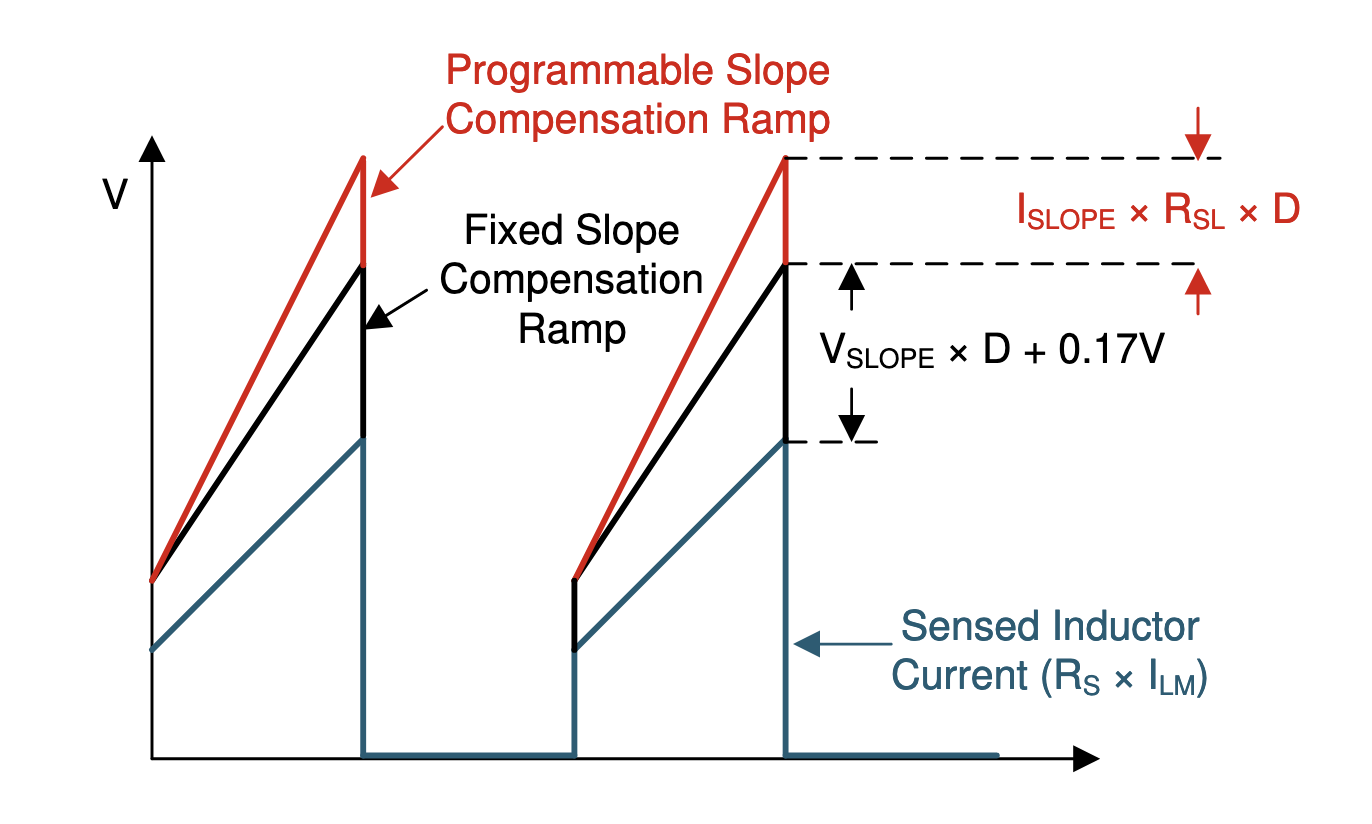
According to the control theory of the current programmed mode, there is an inherent instability when the resulting duty cycle > 1/2. To fix this problem, an artificial ramp is added to the sensed current (or equivalently, the ramp is subtracted from the threshold limit). The same result requires the slope of artificial ramp to be at least half the slope of the inductor current in the off-state. From the off-state diagram in the details section, the off-state voltage across the magnetizing inductance is -V/n, so the magnitude of the off-state current slope is V/(n*L). The requirement for the artificial ramp can be expressed like this:

Here Rs (the sensor resistor) is included since all currents are observed relative to the sense resistor. The LM5155 datasheet doesn't state the artificial ramp slope, but it gives the amplitude of the voltage ramp, which is 40 mV. As slope = rise / run, the right hand side can be replaced with the magnitude of the ramp divided by the period of a switching cycle (or multiplied by the switching frequency):

This places a limit on the sense resistor to achieve stability. Plugging in the values from the datasheet and the design so far, Rs must be less than 16 mΩ. Derating this value by 20% as recommended in the datasheet yields Rs < 14 mΩ. On the other hand, when the peak inductor current hits the threshold,

The DA2032 transformer's saturation current is 3 A, so the required sense resistor is 33 mΩ.

Is all hope lost? No! By adding a series resistor to the CS pin, additional artificial ramp can be added. An internal 30 µA current source drives a voltage ramp across this series resistance. To find the right values for the sense resistor and slope resistor, two equations must be solved simultaneously for Rs and RSL:

In the above, beta is the slope factor, which the datasheet recommends using 0.82 (recall 0.5 is the minimum for stability). Solving for the same maximum current condition yields Rs = 18 mΩ and RSL = 1 kΩ.

Additionally, the LM5155 datasheet recommends a low-pass filter on the CS pin. They state this design recommendation for the RC filter:

All this means is that when the sensed current drops to zero in the off-state, the filter should get at least 3 x the filter time constant to discharge the capacitor. Additionally, it makes sense to have R be small compared to RSL since it appears in series with it. I picked R = 20 Ω, which requires C < 11 nF at the maximum duty cycle of .773. I chose C = 4.7 nF for an extra margin.

While most parts will be chosen downstream of design decisions, several other parts will need to be chosen early and will drive other design decisions. The big parts we need to sort out first are the controller, the transformer, the MOSFET switch, and the diode.

The controller

As noted in the project brief, one reason I took up this project was to design something with the LM5155, a new boost/flyback/SEPIC controller that TI started offering in 2019. From my standpoint, it offers a number of improvements over the controller I used for a previous DCM boost controller, the LM3478. Several of the datasheet figures regarding the current-programmed mode threshold are a lot tighter on the LM5155. The soft-start feature of the LM5155 is adjustable and easy to design around. The LM5155 also supports a wider switching frequency range and very low voltage operation, though I won't be pushing either of those limits.

The transformer

Based on the formulas for the flyback converter output voltage, the turns ratio of the transformer has a big impact on the voltage conversion ratio. This is good because we can get a large conversion ratio without an excessively high duty cycle, and the LM5155 has a upper limit on the duty cycle of about 85-90%.

The transformer will also put an upper bound on the amount of output current the converter can support. From the formula on inductor current, the average inductor current is n/D' times the load current. The actual inductor current ramps up and down over the switching cycle, often significantly, so we need to pay attention to the peak current and keep the transformer core from saturating. The combination of the inductor current ripple, and the limits of the transformer will also drive the choice of a switching frequency.

There are only a few commercially available transformers that have a high turns ratio (n = 10), can support a high secondary voltage, and support decent amounts of the current. These transformers were built specifically for the LT3750 high voltage capacitor charger circuit, which is pretty close to our application, but is designed around applications where the capacitors are discharged almost instantly -- think of a camera flash. The suitable transformers I found were:

• Coilcraft DA203x series: DA2032, DA2033, DA2034
• Wurth WE-FB series: 750032050, 750032051, 750032052

For now, I want the converter to support up to a 30 mA output current, which ought to be enough to drive 10 smaller Nixie tubes with room to spare. Lower input voltage means higher currents, so the maximum current will be seen at the lowest input voltage, which I decided to put at 5 V.

Using the formulas at the end of the details section, at 5 V input and 30 mA output with n=10 turns ratio, D = 0.773 and IL = 1.32 A. If we allow up to a 50% current ripple, the peak current is 1.98 A, so for some headroom, something rated for about 3 A is good.

The DA2032 fits this spec exactly. The Wurth transformers do not list saturation current, but given the physically similar size, it's probably close to the Coilcraft part. The 750032050 has nearly identical specs to the DA2032 (price, inductance, DC resistance, and leakage inductance). The 750032051 has lower leakage inductance -- more on why this is important later -- but it's quite expensive. Unfortunately, none of these have compatible component footprints, and they are too large to place all on one board to pick and choose later, so I committed to the DA2032 since it meets the requirements and is low cost.

The MOSFET

One advantage of the flyback topology, compared to the boost converter, is that the switch doesn't need to block the full output voltage, so a lower-voltage, higher-performance part can be used. High performance, for a MOSFET, means lower on-resistance or Rds(on), and lower gate charge and capacitance (Qg). The Vds figure needs to withstand the off-state voltage of Vg + V/n, as seen in the diagram in the details section. With a maximum design input voltage of 12 V, and an output voltage of 170 V, and the 1:10 transformer, the MOSFET needs to be able to block 29 V. Some headroom is required, because between the leakage inductance of the transformer, and the output capacitance of the MOSFET, there will be ringing and overshoot when the switch turns off, unless attenuated by a snubber, and this can damage the MOSFET if the peaks exceed its Vds limit. The ringing is actually worse at lower input voltages, since it starts with the energy in the leakage inductance that is built up during the on-stage. The energy in an inductor is proportional the square of the current, which is higher at lower input voltages.

MOSFET technology continues to advance, and some of the latest and greatest switches are in Infineon's OptiMOS 6 lineup. These parts offer Rds(on) figures below 6 mΩ, and some Qg figures below 10 nC, though they are presently limited to 40 V. While it is tempting to pick the lowest Rds(on), I prefer to minimize the Qg figure at the highest Rds(on) I can tolerate, to get cleaner waveforms and have less agressive snubber circuits. For this reason, I chose the 5.9 mΩ/9.4 nC part, the BSC059N04LS6. The "BSC" is actually the larger of two packages available, but for an evaluation board, I prefer a larger part (easier to rework and probe) and there's always the option to miniaturize for a more mature board later.

The diode

While the MOSFET gets off easy, from the on-state diagram in the details section, the diode is reversed biased with a voltage of (V + n*Vg). When Vg = 12, the diode has to block 290 V! While Schottky diodes are usually the first choice in switched-mode power supplies, they are limited to lower voltages (< 200 V), so we'll need to choose a super-fast rectifier with at least a 400 V rating and deal with any consequences of diode reverse-recovery. Since the peak inductor current at the primary is about 2 A, the secondary current should not exceed 200 mA, and a 1 A rated diode should suffice. The fastest diode series I found was the ES1 series, offered by several manufacturers. The ES1G is the 400 V part, and I chose the version from ON Semi in the familiar SMA/DO-214 package.