Here is the challenge!
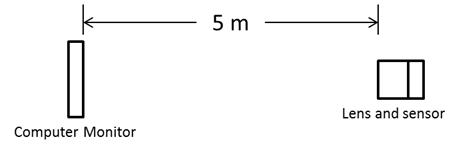
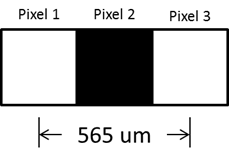
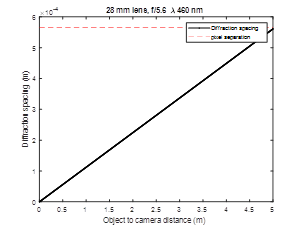
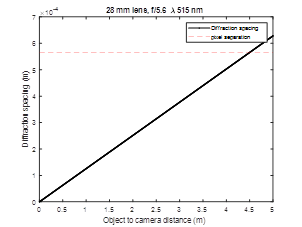
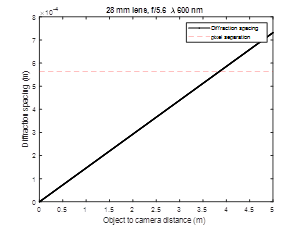
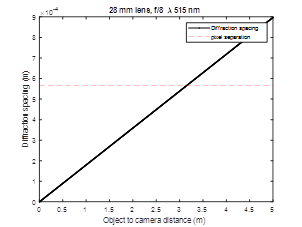
A computer monitor with a width of 0.475 m is placed at one end of room. The maximum resolution of the monitor is 1680 pixels across the width, therefor the pixel width and height are approximately 283 um. A lens and imaging sensor are placed 5 m away from the monitor, and the monitor is imaged. The lens has a fixed focal length of 28 mm lens, manual focus ring, and manual f-stops at 2.8, 4, 5.6, 8, 11 and 16. The image sensor is a Sony IMX219PQH5-C. This sensor was chosen because it has a relatively small unit cell size of 1.12 um. The experimental setup is shown below. I placed the results in the instructions sections.
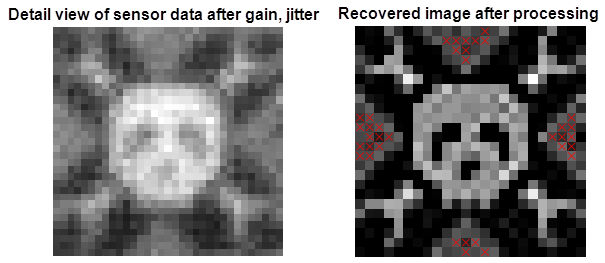
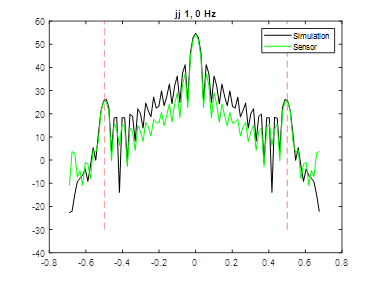
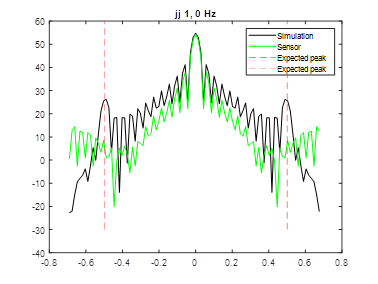
At the diffraction limit, I was able to reconstruct the image in the mean square error sense...yeah!








 Yann Guidon / YGDES
Yann Guidon / YGDES
 Christoph
Christoph
 Cloud4RPi
Cloud4RPi
 Bharbour
Bharbour