-
1Diffraction
Diffraction Limit
The angle for the diffraction limit is:
Angle = 1.22 lambda / D
(source: http://hosting.astro.cornell.edu/academics/courses/astro201/diff_limit.htm) where angle is the angle in radians, lambda is the wavelength, and D is the diameter.Figure 2 Diffraction limit angle.
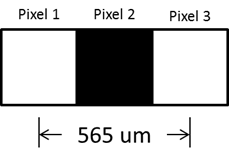
The diameter, D, is taken to be f / f_num where f is the focal length 28 mm, and f_num is the f-stop setting for the lens (2.8, 4, 5.6, 8, 11, and 16). For a computer monitor, the separation between two point sources can be as low as 2 times the pixel width, that is, approximately 565 um.
Figure 3 Computer monitor point source spacing.
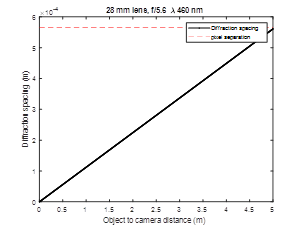
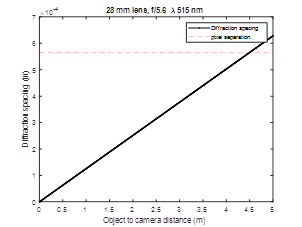
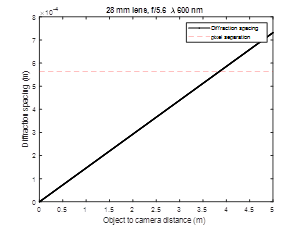
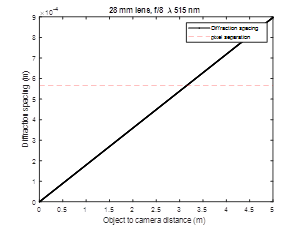
If we consider a setup where we vary the distance between the monitor and the sensor, then we can find the diffraction limit for imaging the monitor. For example, if the sensor was very close to the monitor, then the pixel spacing for the monitor could be very small. The larger the separation between the monitor and the sensor, the larger the pixel size needed to be able to capture it. The pixel spacing for the particular screen is shown as the horizontal dashed line. The wavelengths were selected based on the peak responsivity of the imaging sensor pixels, 460 nm for blue, 515 nm for green, and 600 nm for red. With a f-stop setting of 5.6, then we are very close to the diffraction limit at 5m. Since the f-stop setting is mechanical, we can expect some error in the setting. So, measurements will be presented for a setting of 5.6 and 8.
Figure 4 Diffraction limit for a f-stop setting of 5.6.Figure 5 Diffraction limit for a f-stop setting of 8.
Another way to understand the diffraction limit is by the considering the frequency response of the aperture. This response is found to be something like sinx/x (source: https://scholar.harvard.edu/files/schwartz/files/lecture19-diffraction.pdf), which means that above a certain “frequency” of pixels (or spacing of two pixels), the information at the monitor will be cut off. So, trying to go from the sensor data back to the image on the monitor will be ambiguous. The best we can do is to find an estimate of the image based on some criteria. -
2Imaging
Imaging
A few issues presented themselves with respect to imaging.
Monochromatic sensor
First, a monochromatic sensor was not available for experiments. To keep the resolution high enough at the sensor, all pixels were color gain balanced to operate as if the sensor was monochromatic. While not optimal (since each color of the image sensor would have a different response), results were satisfactory. The color gain balancing was done by including a square of “white” pixels on the screen large enough such that the response of the aperture had reached steady state at the imaging sensor.
Spatial Jitter
Given the distances involved, and the sensor mounting on the PCB, there will be some movement of the monitor relative to the sensor. To track the spatial jitter, a test pattern was placed close to the imaging area. Typical jitter was on the order of 2~3 sensor pixels, and varied during the capture since the experimental setup temperature fluctuated during the heating season.
Spatial Sampling
In order to ensure a sufficient number of sensor pixels were present for each monitor pixel, two squares with large spatial separation were present on the monitor in order to estimate the number of sensor pixels for each monitor pixel.
Monitor Standard Image
Below is a sensor view of the monitor. As mentioned above, the two squares on the outside were for determining the spatial sampling ratio. The left grid image was spatial jitter tracking. The color gain was done with the large square of white, and the image area was the area of interest for recovering images. There is a bit of illumination difference across the image (the left side is slightly darker than the right).
Spatial Sampling Jitter Image Area Color Gain Spatial Sampling
Figure 6 Raw sensor data.
Sensor noise
To determine the sensor noise, the image area on the monitor was set to a solid grey-scale value of 0.2, 0.4, 0.6, 0.8, 0.9 and 1 (where 1 is the maximum rgb value for the monitor). The color gain area was set to 1. The sensor “shutter time” parameter was set such that the color gain area digital values were below the clipping value of 1023. For each setting (0.2, 0.4, etc.), 32 sensor images were taken to determine the standard deviation of the noise. After color gain normalization, the sensor value varied from near 0 up to approximately 0.9 (0.9 and not 1 owing to a slight brightness variation in sensor illumination from one side to the other of the sensor data). The area of interest was 16 x 16 sensor pixels. Within that area, the maximum standard deviation was found to be approximately 0.04.
Figure 7 Measured standard deviation of noise.
When the image area of the screen has an image of interest (instead of a solid square), the signal varies around a sensor value of approximately 0.4. At this sensor level, the standard deviation is approximately 0.03 or 20 log10(0.4 / 0.03) = 22 dB. With a color gain monitor setting of 1.0, imaging a solid bright square without clipping is allowed. If the statistical properties of the image of interest were known, then the color gain setting could be reduced from 1.0 to something lower (and hence increase the shutter time) to raise the digital sensor values and improve the signal to noise of the measurement.
-
3Measurement of Stripe Pattern
To check the diffraction limit, a simple stripe pattern was displayed in the image area of the monitor. The stripe pattern was 101010… across each row.
Figure 8 Stripe Pattern. After color gain, and spatial jitter removal, multiple images can be averaged together (in this case 1024) to reduce the noise. Since there is a fractional relationship between the number of sensor pixels and the number of monitor pixels, it is a little difficult to directly observe the 101010… pattern in the sensor data.
Figure 9 View of sensor data after color gain and spatial jitter tracking.
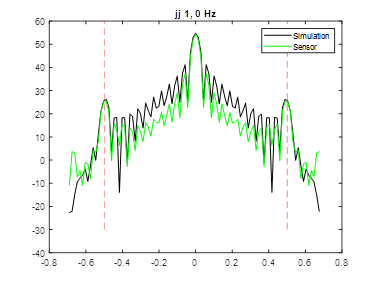
It is easier to take the 2D FFT, and observe the expected peaks. Below is the first row of the matrix obtained from taking the 2D FFT of the sensor data. The horizontal “frequency” grid is related to the monitor pixels. So, for a 101010… pattern, one would expect peaks at 0.5 and -0.5.
Figure 10 Measurement of Stripe Pattern with f-stop set to 4. Simulation of a stripe image with fractional sampling shown for reference.
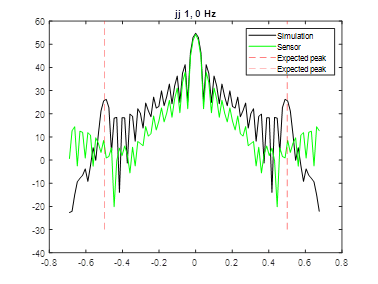
Changing the f-stop setting on the lens to 5.6 gives the image and fft2 result below. The stripe pattern is still visible in the image, and in the ff2 view, the peaks have been reduced by ~4 dB.
Figure 11 View of sensor data after color gain and spatial jitter tracking.
Figure 12 Measurement of Stripe Pattern with f-stop set to 5.6. Simulation of a stripe image with fractional sampling shown for reference.
Changing the f-stop setting on the lens to 8 gives the image and fft2 result below. The image is more or less solid, and the peaks are completely absent (even with 1024 image averaging).
Figure 13 View of sensor data after color gain and spatial jitter tracking
Figure 14 Measurement of the striped pattern at f-stop 8. Peaks are absent in the sensor data. Simulation of a stripe image with fractional sampling is shown for reference.
-
4Imaging and Reconstruction
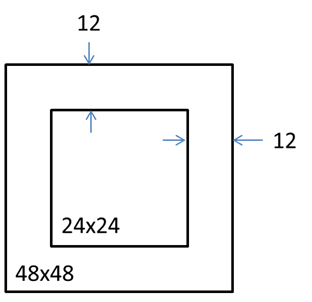
The next step is to attempt to recover the image. The image area in total is 48x48 monitor pixels. The 48x48 image is made up of a 24x24 image of interest, and a 12 pixel border of random values.
Figure 15 Image of interest with random border.
The general idea is to acquire a series of random images to train the recovery algorithm, all the while tracking the color gain, and spatial jitter. Once the training is done, then the algorithm is applied to the image of interest.
Figure 16 Original image, sensor data after gain and jitter correction (circles indicate location of image in border of random values), recovered image, error locations (apply hard decision at a level of 0.5), f-stop 5.6.
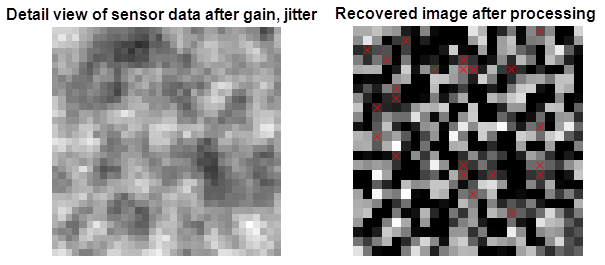
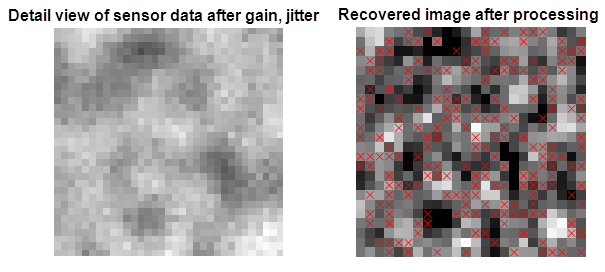
Since the monitor image is made up of 1s and 0s, the signal to noise is sufficient to capture and process the image with no averaging. Below is a detailed view of the sensor data and the recovered image for comparison. The pixels in the red circle bounds of Figure 16 are shown for the detailed view.
Figure 17 Detailed view for comparison of sensor data and after compensator (the ‘x’ symbols indicate error locations when applying a hard decision), f-stop 5.6.
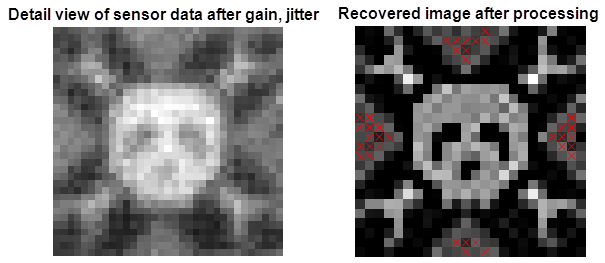
Below is a sample image (the modified logo from the Hackaday website).
Figure 18 View of processing steps and results for Hackaday logo, f-stop 5.6.
Figure 19 Detailed view of Hackaday logo recovery, f-stop 5.6.
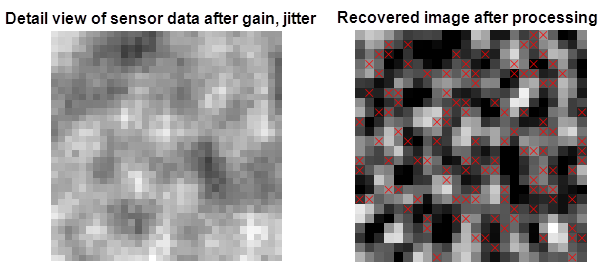
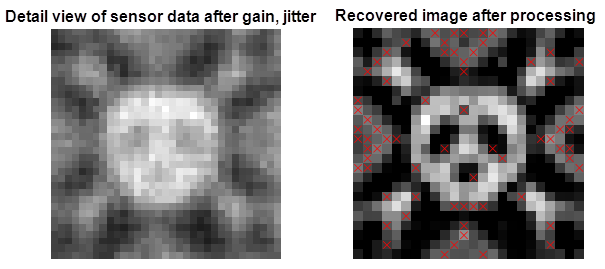
Next, moving to a f-stop of 8 heavily filters the data, but some details can still be recovered in the mean-squared sense.
Figure 20 Processing steps for the random pattern, f-stop 8.
Figure 21 Detailed view of the results for the random pattern, f-stop 8.
Figure 22 Processing steps for the Hackaday logo, f-stop 8.
Figure 23 Detailed view of the Hackaday logo, f-stop 8.
Out of interest, the processing was also done for f-stop 11.
Figure 24 Processing steps for the random image, f-stop 11.
Figure 25 Detailed view of the recovered random image, f-stop 11.
Getting Cozy with the Diffraction Limit
Do you hate the diffraction limit when you take an image of a scene? Me too! Here is a story of trying to do my best to correct it!













Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.