Background and motivation
In 2021/2022 I designed a DC electronic load that would be more capable, but also much more complex than the usual DIY solutions. However, after building a working breadboard prototype of the analog circuitry with 12 ICs including multiple precision and dual opamps, I thought that it might be better to start with a smaller project that would allow me to gain a lot of experience and write much of the non-application specific code that I could use later on for the digital part. Also, at the time I was looking for a decade resistor box to add to my lab. And this is how I started working on a programmable decade resistor, a pretty specialized tool for niche applications.
Introduction
A programmable resistor is a electronic device whose electrical resistance can be adjusted typically through digital signals. Programmable resistors are available in form of integrated circuits (often referred to as digital potentiometers) as well as stand-alone devices/expansion cards. There are many different applications, each with their own set of requirements e. g.:
- programmable gain amplifiers
- sensor emulation
- hardware-in-the-loop simulation (detailed explanation below)
- calibrators
- prototyping
Basic concept
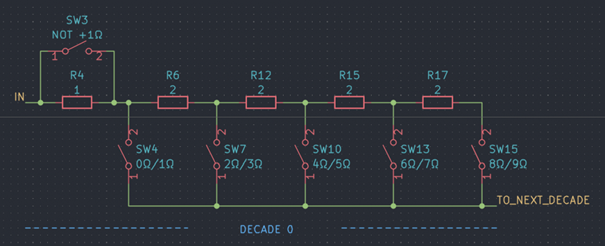
The programmable resistor closely follows the main principle of resistor decade boxes: connecting multiple devices (“decades”) in series, with each of the devices having a settable resistance of 0 Ω, 1 ⋅ 10n Ω, 2 ⋅ 10n Ω, 9 ⋅ 10n Ω, where n specifies the decade in question.
Those devices are simple resistor networks complemented by one (multi-throw) or more (single- or multi-throw) switches. While the actual topology and resistor values vary vastly, the switch(es) will always either short out or connect certain resistors or simply tap certain nodes of the resistor network. A simple implementation uses a 10-throw rotary switch to tap the nodes of a series resistor network of nine resistors.
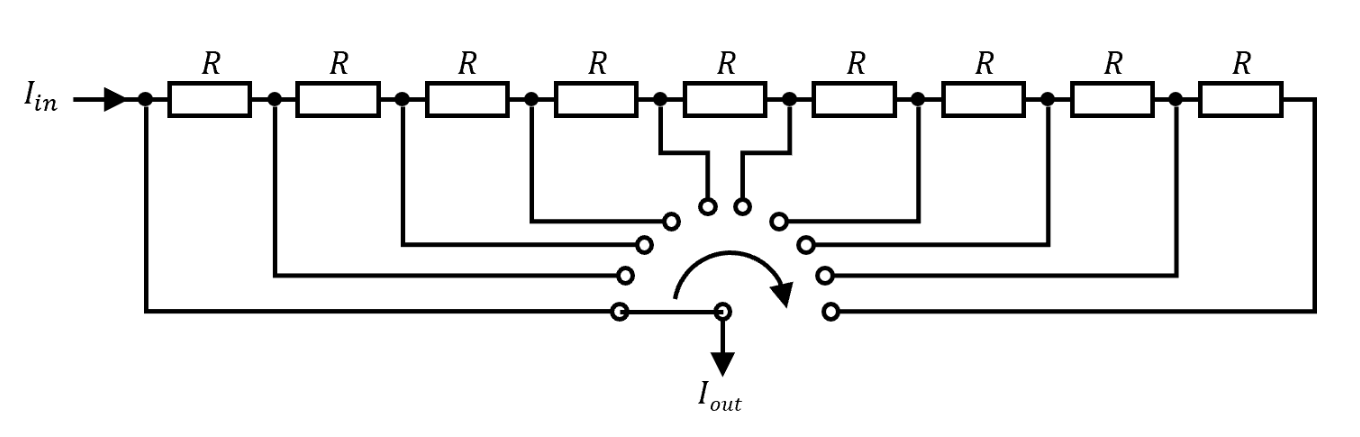
Features
| Parameter | Value / Description |
|---|---|
| Range | short circuit, 1 Ω … 999.999 kΩ, open circuit |
| Setpoint resolution | 1 Ω |
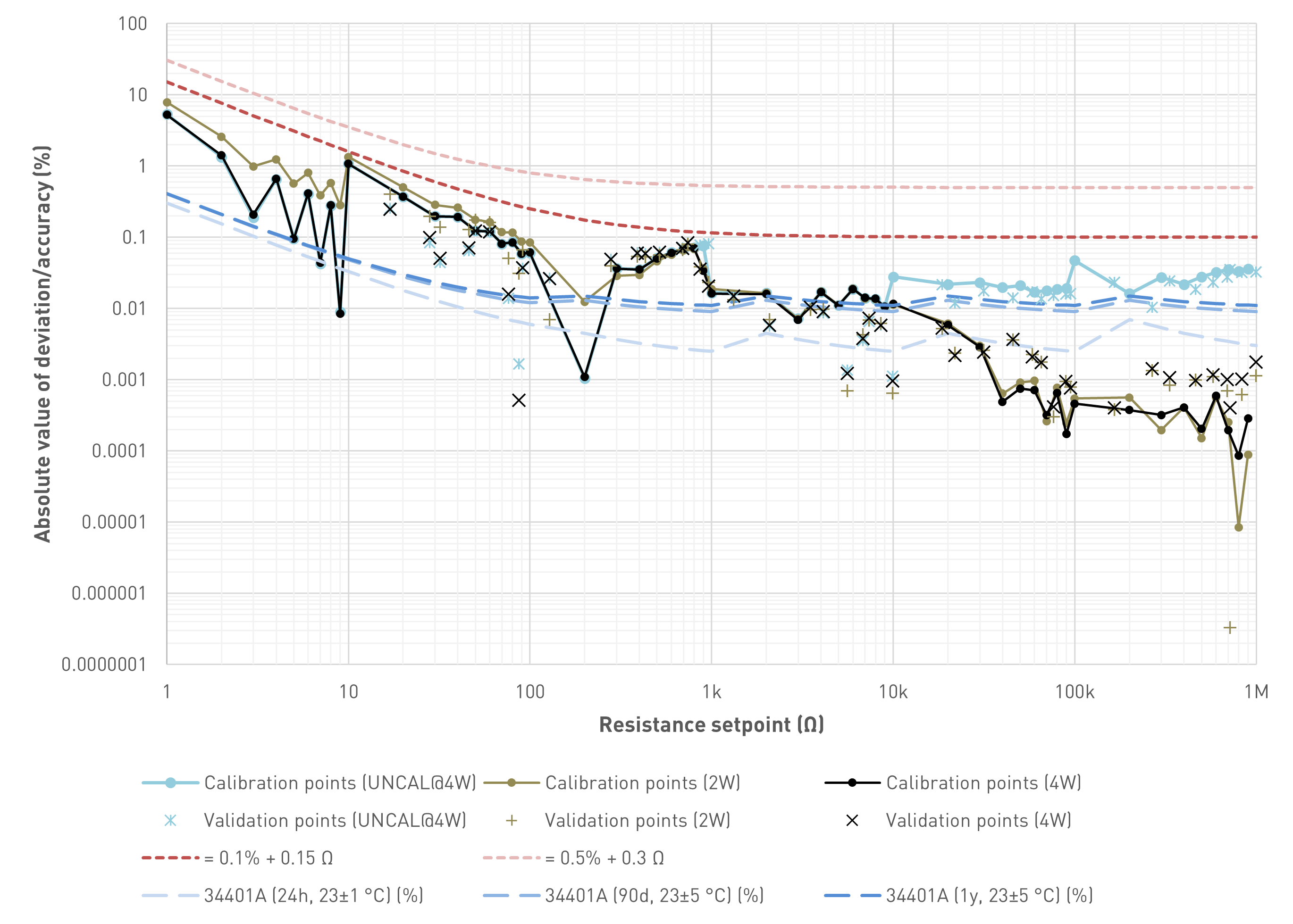
| Short-term setpoint accuracy estimate | <=±0.1% of value + 0.15 Ω (2W and 4W). The estimate is based on measurements for a limited number of calibration and validation resistance setpoints. Measurements performed with an Agilent 34401A 6.5 DMM for a single DUT. Note: This is NOT a valid strategy to get reliable/reproducible results in the sense of a specification. It's just a more or less plausible envelope based on measurements I took for my prototype. The initial goal was achieved: (much) better than ±0.5% of value + 0.3 Ω |
| Display value resolution | 6.5 digits, 5.5 digits, 4.5 digits, 3.5 digits, but not better than 1 mΩ |
| Short-term display accuracy estimate | <=±0.01% + 0.025 Ω (2W and 4W). This figure is meant to show how much the displayed resistance value (that is based on a calibration) deviates from the value shown on the DMM, the calibration has been performed with. |
| Thermal drift (estimate based on design) | <<50 ppm/K |
| Power rating | >=0.2W for decade 0 (0..9Ω), >=0.5W else Exact value depends on setpoint (shown on display) |
| Bandwidth | unspecified |
| Calibration modes | - Uncalibrated: Switches are activated according to entered setpoint, display shows setpoint - Two-wire (2W), Four-wire (4W): An internal setpoint is calculated based on the calibration values to reduce the error (effects changes for higher resistance values only) |
| Operating modes | Fixed: On trigger, no change Step: On trigger, step to trigger setpoint value Up: On trigger, increase setpoint (linearly, 1-2-3-4-5-6-7-8-9, 1-2-5, 1-3) Down: On trigger, decrease setpoint (linearly, 1-2-3-4-5-6-7-8-9, 1-2-5, 1-3) List: See list mode |
| List mode | Up to 100 values with individual dwell times - Start: on trigger; or immediately after mode selection... |
 Sebastian
Sebastian













1) Fantastic project, and very well documented too! 2) How'd you draw the block diagram that's on github? It is quite pretty :)