Surface Normals from Stereo Polarimetric Images

A single polarimetric image gives us information on the polarization angle, per pixel. With the angle of polarization we can calculate the Plane of Incidence. This plane contains the surface normal and the propagation vector of the incoming radiation. We can't calculate the surface normal from just the polarization angle / plane of incidence in a single image.

However, if you use 2 images that look at the surface from different angles, you get 2 Planes of Incidence. The intersection of these 2 planes is a single line. Because this is the only line shared between the 2 planes, and because each of the planes holds the surface normal, the surface normal must equal the intersection of the 2 planes.

It looks something like this. Given 2 cameras, red and green, we show the plane of incidence from both viewpoints. Because of how reflection works, the line between the sensor and the surface also lays in the plane of incidence, which is why this plane shows up as a line for the sensor, corresponding to the angle of polarization.

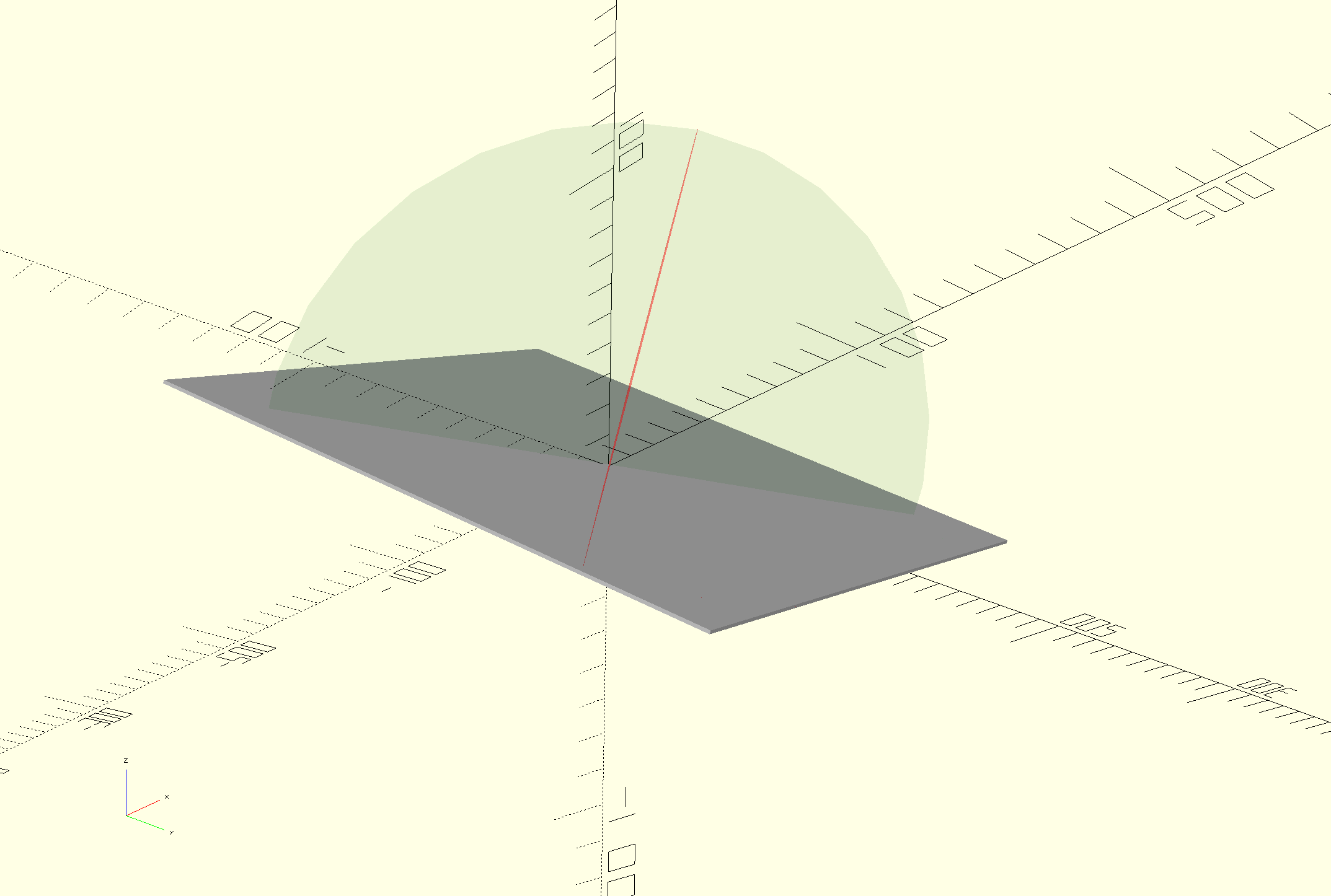
View from the red camera. Ignore the green circle, this is the plane of incidence for the green camera.

View from the green camera. Ignore the red circle, this is the plane of incidence for the red camera

Now that we have the polarization angles for both cameras, we can use the intrinsic parameters of the camera to project a ray to the pixel and calculate the plane of incidence. For both cameras we get a plane, and for each plane we calculate the normal to the plane (both of which are tangent to the surface). Finally, we take the cross product of these normals (tangents) to retrieve the surface normal.

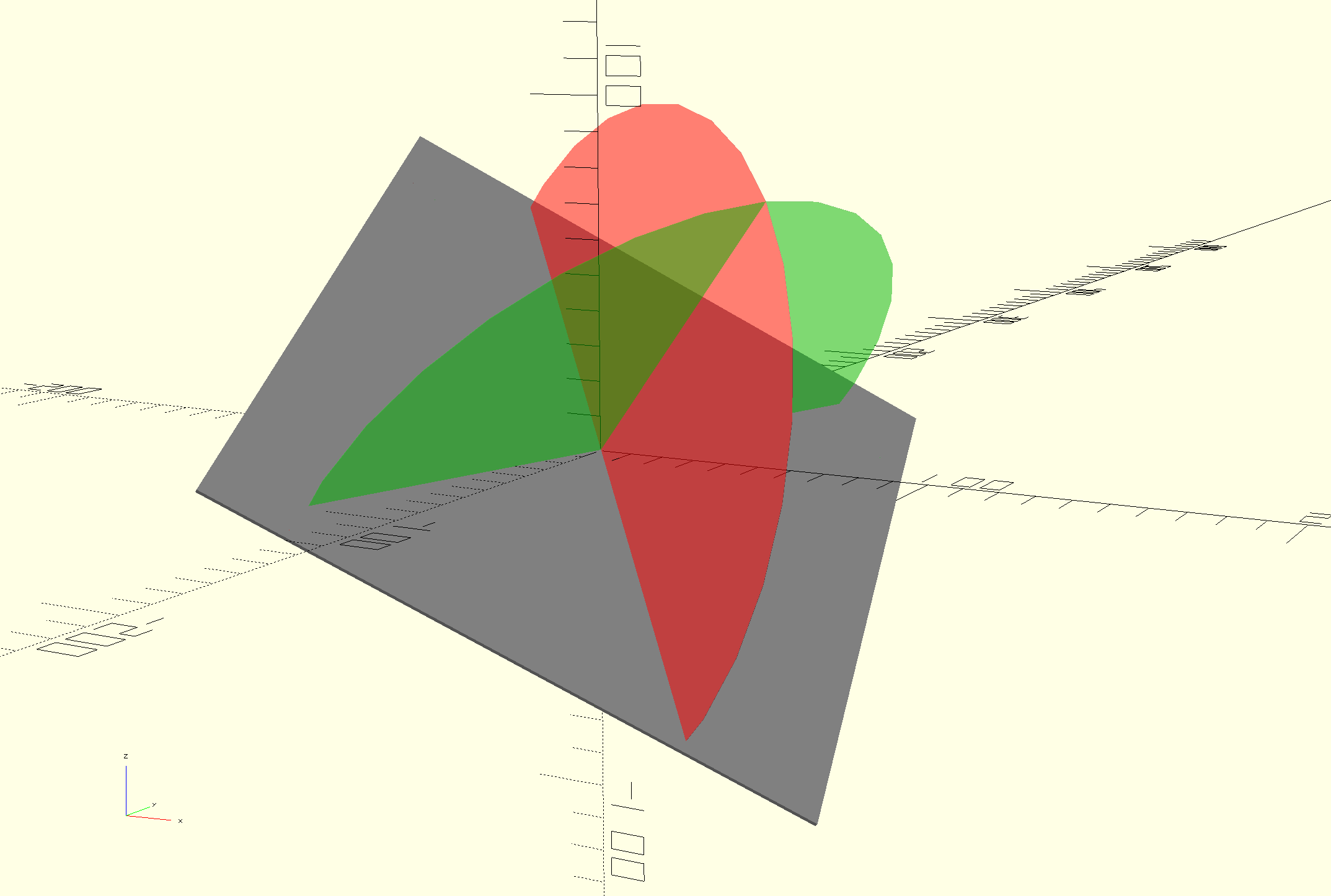
The surface normal is equal to the intersection of the 2 planes of incidence

Now, there is a caveat: when the planes of incidence become closer in terms of angle with respect to each other, opposed to (ideally) orthogonal, any noise in the signal will have a larger effect of the calculated surface normal. We offset this by using the feature of cross products that the absolute value of the vector decreases as the angle between the 2 source vectors decreases. We use this as a measure of "confidence" or "weight".