Hi all,

This update will show how we're calculating the max distance possible using this communication method. We also have changed the IR LED (again) to get a cost savings and an improvement in communications distance.

To calculate the max distance our SAO is expected to be able to communicate we, used this document from Everlight . The equation for distance is on page two as: 

This looks a bit funky but if we break it down it makes sense. dmax is the maximum distance we expect the transmission to work at. We'll be using meters in this equation. Ie is the Emitter Intensity, or a fancy word for saying how bright the LED is. This is in units of mW/sr, or how much power is needed per Steradian. A Steradian is a really weird measurement but it is essentially like a radian in a 2D circle rotated around the center point of that circle to make a 3D version of a radian. Don't worry if that doesn't make sense, it doesn't for us either. The key part is that at higher Ie, we generate more IR light for the receiver to detect. Eemin is the Receiver Irradiance, or how sensitive the receiver is to light. This is in units mW/m^2, or how much power per area we need to detect IR light. The lower the Eemin is, the more light it can detect and the less bright our IR LED needs to be. 

For our newly chosen IR LED, we need to figure out the Ie. While Digikey does give this to us in the data summary as 150mW/sr @ 100mA, we must limit our circuit to 20mA per output pin on the ATTINY85. Diving into the LED data sheet, we can find the graph below:

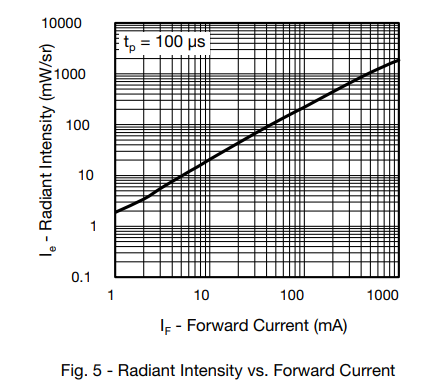
This graph shows us the relationship between the current (x-axis) and the resulting Ie (y-axis). From this, our Ie will be around 40mW/sr. Be careful about reading this graph, both the x and y axis are logarithmic, meaning they don't change as one might expect. Going diagonally on this graph greatly increase both the x-axis and y-axis. One thing to note here is the looking at the 100mA line, we see it crosses over around the 200mW/sr. Digikey was showing the min Ie of 150mW/sr in its summary and this LED may be brighter than this as that value takes into account the variance possible in this LED.

Now we need to find the Eemin for our receiver. This can be a bit tricky to find but one of the reasons we chose this specific IR Receiver is because it has the graph below that answers our questions:

This graph shows the relationship between the amount of light around the sensor (x-axis) and how sensitive the receiver is (y-axis). Be careful here, the x-axis is logarithmic while the y-axis is linear. Going to the right increase much faster than moving up the graph. One of the reasons this graph is helpful is that it specifies how bright daylight is (10 W/m^2) and what wavelength is assumed (950nm). Since daylight is the worst case scenario we expect this SAO to be used in, we can follow the 10W/m^2 line up to around 1.5mW/m^2 Eemin. Since the 950nm wavelength estimated for ambient illumination is close to our IR LED's wavelength of 940nm, we should expect this graphs relationship to hold for our setup. Note that this is our worst case sensitivity, if we're in a darker environment than daylight, the sensor will be more sensitive. This makes sense as our sensor has less light hitting it, thus less noise that may interfere with the signal. 

With all of the required values found, we can now calculate the distance as:

This isn't too bad, it's about the length of a standard bedroom. We expect that most people will use this indoors and will get more range than this. One thing to note is that while 20mA is the safe current for the ATTINY85, a single pin can technically go up to 40mA if we change the resistor. This could get us a Ie around 90mW/sr and a theoretical range of 7.746 meters in sunlight. We don't recommend this but if anyone does try this, let us know how it works.

Now that we know the distance, we need to find the new resistor value for our LED. We used Kirchhoff's current and voltage laws to calculate the resistor size for the LED with a supply voltage of 3.3V, forward current of 20mA, and the LED having a forward voltage (how much voltage the LED "uses" when lighting up) of 1.35V. I say using Kirchhoff's laws, but Digikey's LED in series calculator is faster than doing it by hand. We do need to be careful here though as the ATTINY85 does not output a constant 3.3V per unit of current. It actually outputs around 2.25V at 20mA as seen in the graph below:

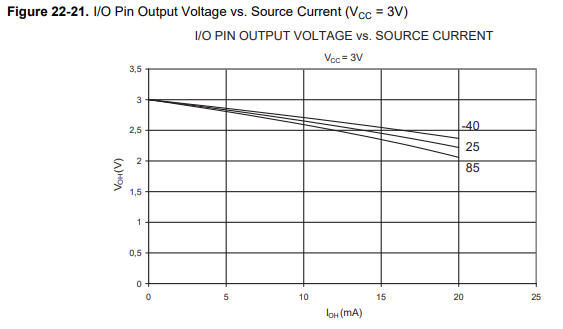
Putting all of these values in gets us around 97.5 Ohms, giving us the new circuit diagram and parts list below:

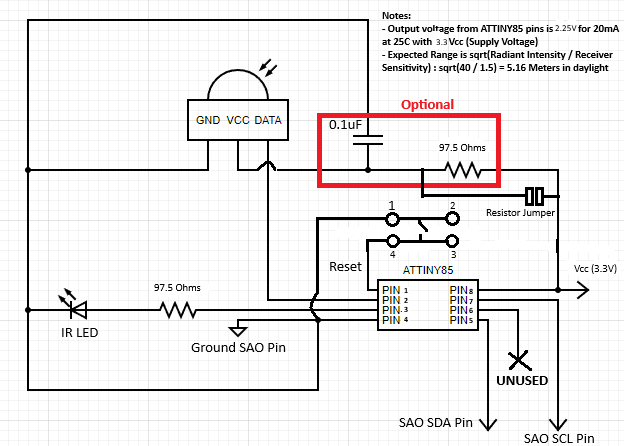
Parts List:

• https://www.digikey.com/en/products/detail/microchip-technology/ATTINY85-20PU/735469
• https://www.digikey.com/en/products/detail/vishay-semiconductor-opto-division/TSOP58238/4695679
• https://www.digikey.com/en/products/detail/vishay-semiconductor-opto-division/TSAL6102UL/20379899
• https://www.digikey.com/en/products/detail/kemet/C320C104K5R5TA7303/3726160
• https://www.digikey.com/en/products/detail/yageo/MFR-25FBF52-97R6/12793
• https://www.digikey.com/en/products/detail/cui-devices/TS02-66-50-BK-260-LCR-D/15634249