I'm working on PRNGs these days.
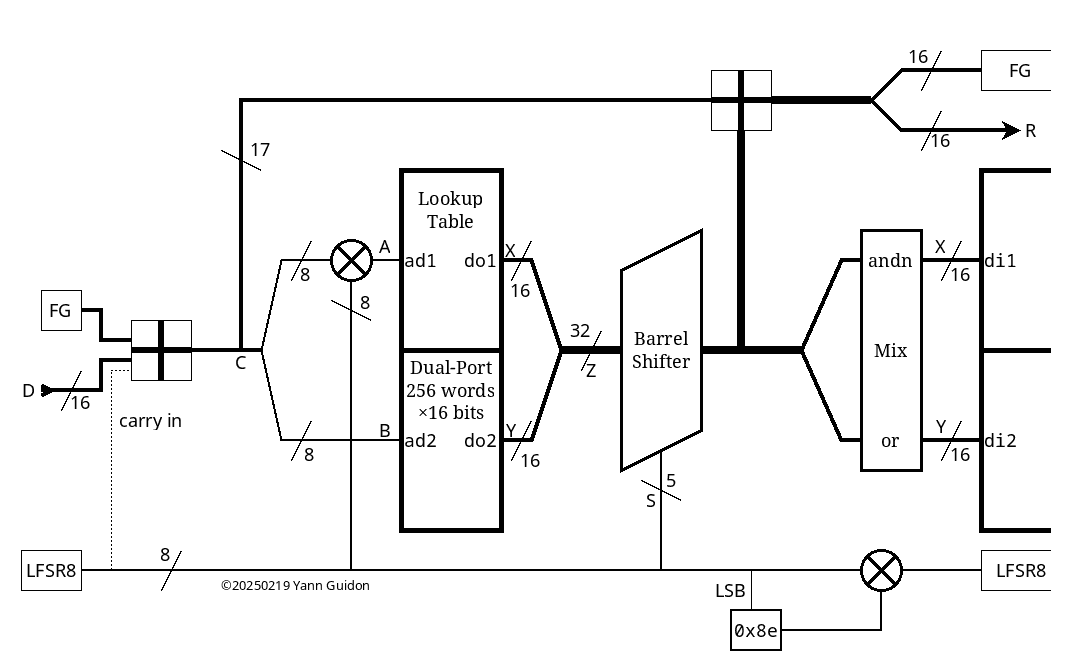
I have made a replacement for the POSIX rand() and srand() functions (see log a POSIXy rand() ) using a mixed structure: a basic 32-bit LFSR PRNG has its LSB mixed with a PEAC 16x2 scrambler, outputting 16 bits (15 due to POSIX) with little effort and 65 bits of internal state. I want to make it even smoother and the best way is to add another scrambler with a very different structure. Naturally I remembered the RC4 stream cypher and a table-based system looks interesting, with its very large state and apparent simplicity. Though I'm not doing a cypher and I have forgotten the details. And memory accesses are expensive, particularly 16bit ones.
Anyway, a 256-byte table is nice but my algo works with 16 bits at once so a sort of "parallel RC4" would be required. I don't want to have to deal with key initialisation so let's just borrow the SBoxes of AES : one is forward, the other is reverse, let's put them in parallel as they are reciprocal permutations. They must be pretty good, I assume.
So with this system, I parallelize two table lookups, which is "good" for modern microprocessors, and the state is extended to 512 bytes, a bit like RC4A. But wait : if one has to swap values, then BOTH tables should be accessed by the same two indices. So the pair of tables is turned into a double-width, dual-port LUT (but I can do that with a FPGA, no biggie). This leads to a new structure that provides 2×16=32 bits per dual access: now the table works as an expansion table!
The extra 16 bits can be reused :
- as extra parameters for the "swap" which is now a 32-bit rotation / circular shift
- as offsets for the address inputs
With this extra feedback, the system becomes almost self-sufficient and can output a reasonable stream when fed with a constant (or short cyclical) value. Using a rotation instead of a swap is another "nice touch" that upsets the usual balance of a permutation, yet preserves the total number of set bits.
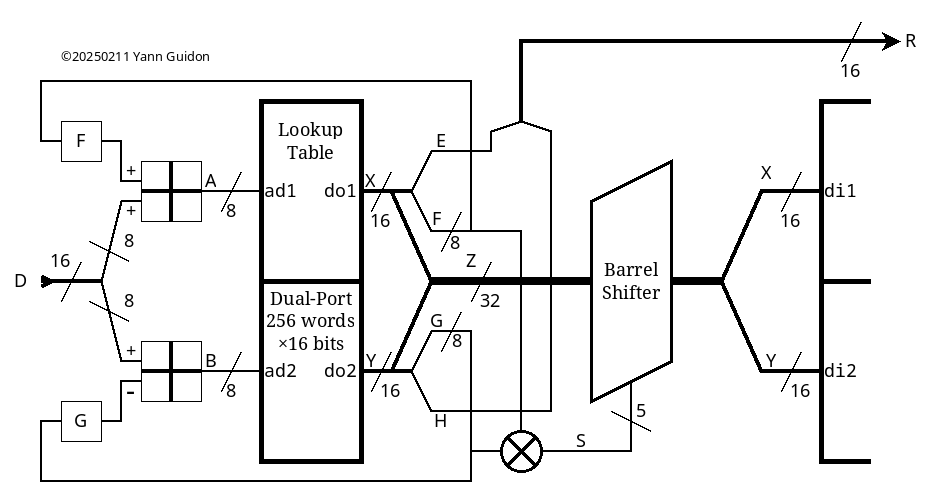
Even though the LUT starts with a pair of AES SBoxes which are permutations, the goal is only to fill the table with a well-behaved array with as many 1s as 0s. The rotation keeps that balance but the system does not rely on the table being a perfect permutation. In some degenerate cases, the entry should have at least a few bits set, no 0xFFFFFFFF or 0x00000000, that's all.
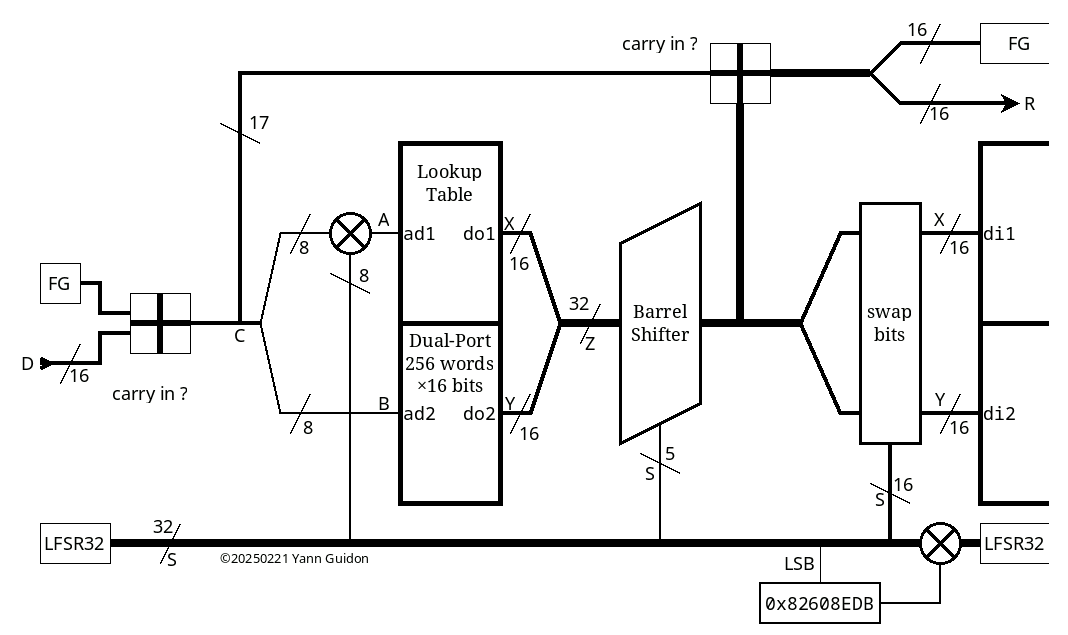
This is not cryptographically secure though, and the primary design assumption was that the input provided a half-decent entropy source (think LFSR or congruential PRNG). But with a careful design (the method to offset the address bits), it can become autonomous.
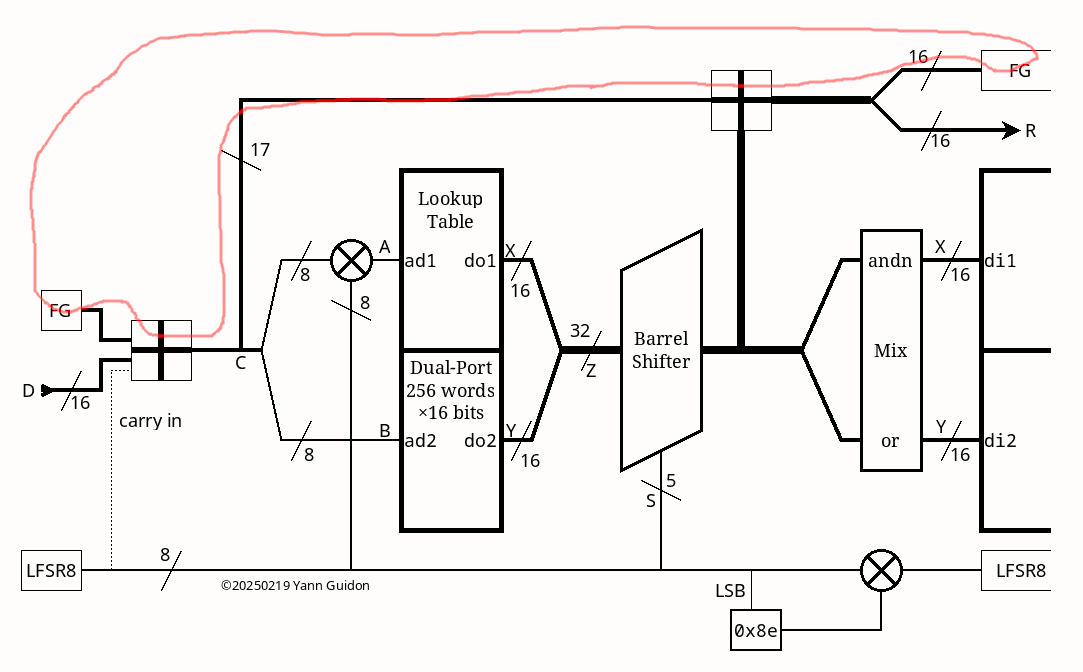
Looking back at RC4, this new algo can compete on throughput (only one read and one write per byte) though it certainly has glaring loopholes (and the code has many word casts). Yet it's still "good enough" for a semi-decent PRNG and the implementation in FPGA is a breeze.
I'm sure enhancements will appear, as I have identified a point or two to adjust...
.
-o-O-0-O-o-
Logs:
1. First log, second stage.
2. Startup
3. v2
4. v3
5. Initialisation
6. ARX
7. v4
8. 3:2 compression
9. Initialisation: the ugly
10. Entropic principles
11. v4.2
12. Feedback
13. so long v4.3, welcome v4.4
14. ...
15. ...
16. ...
17. ...
18. ...
19. ...
 Yann Guidon / YGDES
Yann Guidon / YGDES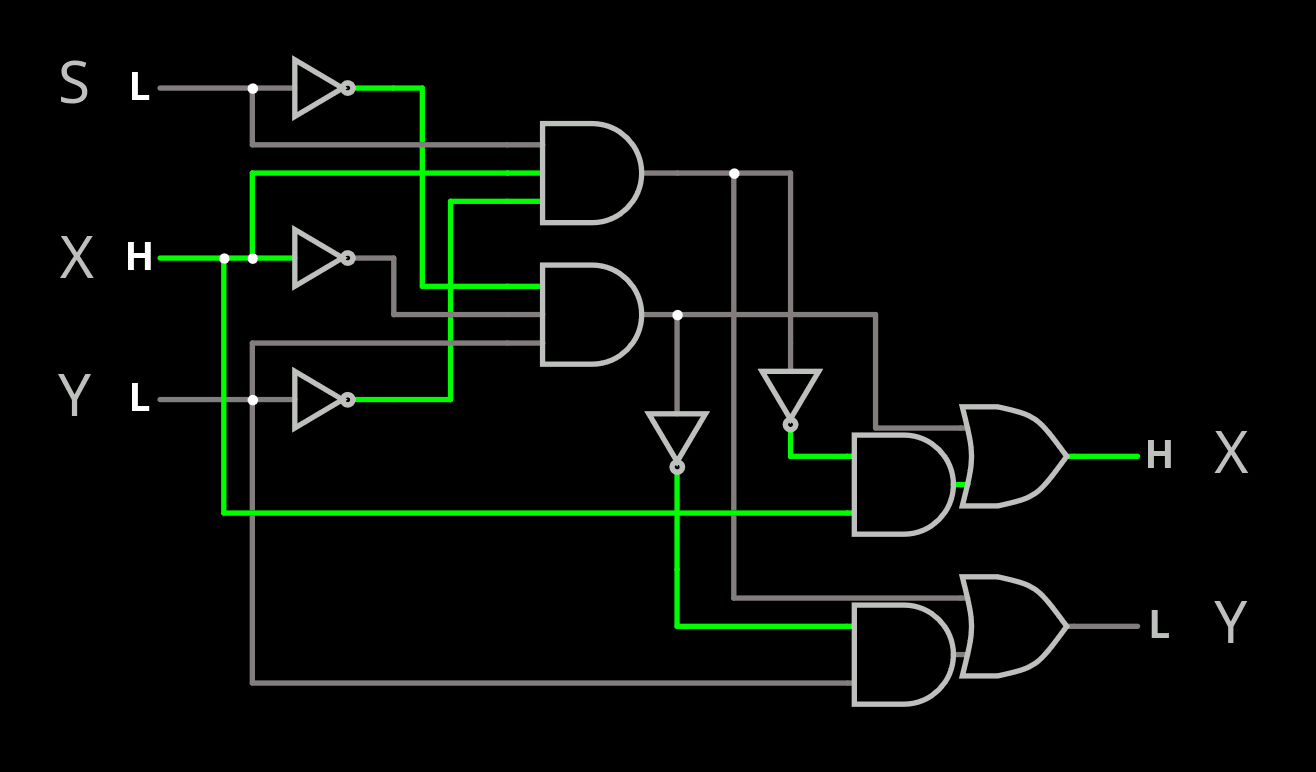



C(n,k) = n! / k!×(n-k)!