low-field MRI

Further updates have moved to another build log:

https://hackaday.io/project/12352-low-field-mri-continued

With the recent success of the OpenCT2, I'm back thinking about the coded aperture MRI again. David was also in Antarctica for a while for his radio astronomy graduate work, but he's been back and we've been chatting about MRI things lately.

The two issues: Coil Winding, and a USB ADC

When the project went on the backburner, I'd hit two stumbling blocks that seemed like good solutions would have to present themselves for before things could progress:

1. Coil Winding: It's much, much more difficult to wind radio coils than it looks. My attempts to do this by hand ended in tears (and very sore fingers).
2. High Speed, High Resolution, Long Capture ADC: It's apparently very challenging to find a high speed (100ksps+, ideally 1 msps+) high resolution (14-16bit) USB analog to digital converter peripheral that can also stream at least several seconds worth of data. Most have very small sample buffers (approximately a few thousand samples)
   

Coil Winding Machine

Just like a prerequisite for becoming a jedi is building your own lightsaber, it seems like a prerequisite for being interested in radio is building your own coil winding machine. Radio coil winding seems like a somewhat lost art (I'm sure if this was a century ago, I'd know a dozen folks who were expert coil winders), but youtube has no shortage of videos of folks who have put together their own machines. It seems that one can also purchase manual coil winders fairly easily, but they tend to look ancient, and like one could come up with an automated design in a few evenings of work.

Being somewhat at the mercy of inspiration, a seemingly simple design suddenly came to me, and after a quick trip to the hardware store for some threaded rod, and by the end of the evening I had cobbled together some leftover Makerslide and Misumi aluminum extrusion into this:

The above half-complete winder allowed was just enough to wind a single-layer coil hundreds of times faster than I'd done it by hand (and nearly perfectly), convincing me that I was onto something.

After another evening slaving over a warm laser cutter, the coil winder emerged:

The different components, drawn from leftover pieces of projects, are the following:

Rotational/Winding Stage (right side):

• NEMA17 Stepper with plenty of torque to draw the wire from the spool (from Inventables, I believe)
• Coil Wedges: Two laser-cut wedges that are tightened around the coil form to hold it in place. I cut these to look like step drills, so the coil would be positioned relatively straight, and there'd be at least a millimeter or two of area to bite onto.
• 5/16 threaded rod, M8 coupler, and large washers/wingnuts (hardware store/ebay)
• Laser cut NEMA17/threaded rod holder that mounts to the aluminum extrusion.

Linear Stage (middle):

• Makerslide linear rail and carriage (from Inventables)
• Plastic syringe and tips intended for solder paste (from Zeph Paste), zip-tied onto the carriage
• 5/16 threaded rod, NEMA14 motor, M8 coupler
• 3D printed carriage/nut holder from the OpenCT2 project
• Laser cut NEMA1/threaded rod holde

Spool Holder (left):

• Heavy wire spool (for tension)
• 5/16 rod, two laser cut holders.

Control:

• Arduino Uno with Motor Shield
• Modified OpenCT2 motion control firmware, with added commands on the serial console for coil winding and keeping track of the number of winds!

The dimensions of the long aluminum extrusion pieces are about 50cm, and the short ones holding each component are about 10-12cm high. The aluminum extrusion makes it easy to resize for larger/small coils, and to move in the tip of the liner stage very close to the coil form during setup.

Winding Coils

Following Bradley Worley's great proton precession magnetometer (PyPPM) project, I decided a good place to start would be replicating his (or a similar) proton precession magnetometer, then experimenting with it under different non-uniform field conditions to see how viable the coded field technique may be. About 10 years ago Stefan and Richard Hollos published a book called Signals from the Subatomic World that also describes building a proton procession magnetometer. Both serve as good introductions and have conceptually similar hardware (even if the specifics are different).

Bradley had success with his version 1 coil, which is a single coil containing 4 layers of 158 turns each (632 turns total). I decided this was a good coil to start with (since I've never successfully wound a coil before), and then I'd work towards winding more sophisticated coils. Bradley specifies using a version 2 "humbucker" coil (two identical but counterwound coils) to cancel out much of the 60Hz environmental noise, which is easily visible on his great first raw plots. The Hollas PPM sensor coil also uses a humbucker arrangement, with similar specifications to Bradley's single coil (4 layers @ 138 turns/layer). The raw data in Chapter 7 of their book looks substantially noisier than Bradley's, but they were doing this a long while ago, and it's not clear whether they were subtracting baseline measurements, which should clean up the data a great deal.

My first multilayer coil (the 4 layer, 158 turn/layer, 638 turns total) turned out much better than I was expecting. The current coil winder doesn't include anything to smooth out the very occasional tiny bump or bend in the wire, so some layers have one or two more winds than others, but the overall packing density was very good, and the coil has a total of 638 counterclockwise winds. Another coil counterwound (to make the humbucker arrangement) will make for a good first set of coils for initial tests, I hope.

To keep the coil windings in place, I used some super glue, then covered the coil in electrical tape -- but next time I'd like to try something better. The superglue didn't bond well to the wire, and the electrical tape obscures observing the beautiful windings!

Analog to Digital Converter

An Earth's field proton precession magnetometer nominally weakly oscillates at 2khz, making an ADC with a sampling frequency above 20Khz adequite. The Hollas PPM uses a 12-bit ADC, where Bradley's uses a 16-bit ADC. Here, because we're interested in trying to spatially resolve the signal using potentially a wide range of frequencies, the requirements are higher. The Nyquist rate for resolving protons in a 1 milliTesla field, which is only about 20 times as large as the Earth's field, is about 84kHz. A 1 megasample/second ADC would give a Nyquist rate equivalent to about a 10 milliTesla field, which seems like it would give some room for experimentation. Intuitively I have no sense of how much frequency range will be required, with it likely relating to a bunch of factors, and so it will likely be best determined empirically through some experimentation.

It's been oddly difficult to find an analog to digital converter that has the following specifications:

• 1 megasample per second or greater (but 100kSps would be okay to start, too)
• 14 to 16-bit resolution
• Ability to record several seconds of data
• Ability to stream the data through an easy-to-use API

I have investigated the specifications for every USB digital storage oscilloscope or DAC that I could find, and while many have substantially higher sample frequencies or sufficient resolution, most attractive solutions (like the Analog Discovery Kit) appear to have not been designed to acquire data for long, and suffer from an extremely low sample memory.

I don't have a great solution for this, but I've thought about starting with a USB soundcard capable of sampling at 16-bit/192Ksps to begin. I've also picked up an Arty FPGA board to tinker with, which includes a fast ADC and a large amount of memory that could be used to store samples -- but creating a high-resolution long-memory FPGA oscilloscope would be quite an undertaking, and I'd rather make my mistakes cheaply and find an off-the-shelf solution. Suggestions are welcome!

As always, thanks for reading!

Let's have a look at the first test rig for measuring magnetic fields over a 3D volume.

I confess that I've been thinking about this for a few weeks, and it's been a fun (and sometimes frustrating) design process. We'd like to accurately map the magnetic field intensity and direction at each location in a small volume -- say a 10cm cube. Normally if you'd like to move something through a volume (say, like a 3D printer extruder), you'd put together three perpendicular linear axes, mount your tool or sensor, and that would be it.

But here, getting accurate readings is very important -- this will ultimately be used to measure the first coded fields, and the accuracy of those field measurements will determine the quality of our reconstructions, and in the extreme case, whether the technique will work at all. And it just so happens that most of the things linear axes are made out of -- stepper motors, lead screws, nuts, and other hardware, are magnetic. So we'll have to think a little unconventionally, and figure out a way to make a scanning system that keeps these components somewhat distant from the scanning volume.

The Z and rotational axes

The base for the rotational stage is mounted on two M8 nylon lead screws that transfer linear motion, and move the whole stage up and down in Z. The base has three 1/4 inch aluminum slides with nylon bushings at 120 degree angles, and there are also three stationary 1/4-20 threaded rods up the length of the machine that help keep everything rigid.

I really like how the rotational (theta) axis worked out -- I had some MLX (2.03mm pitch) timing belts left over from another project, and ended up (after several attempts) being able to successfully laser cut a giant ~5 inch timing pulley (with about 185 teeth) that easily rotates, and also serves as a platform for the radial (rho) stage that we'll see below.

A critical aspect of this stage is that, to make it useful for further testing (of the code coils, or even primary coil), it has to have a large open area in the center where stationary coils could be mounted from the bottom. This complicated the design a bit, but it ends up working out pretty well, and just the Z and rotational axes could very easily serve as the platform for a tiny CT scanner (or other interesting projects that need to rotate around a stationary sample).

Two NEMA14 motors power the Z axis, and are coupled to the nylon lead screws using flexible aluminum couplers.

I like to try and include extra holes and mount patterns on the things that I design so that I can elegantly mount wires or other things as it develops without cutting a new part. Here I've included mount patterns for a Raspberry Pi and Arduino Uno on either side of the bottom of the base.

The lid on the top fits perfectly. Ideally under here there'll be a scanning magnetometer, and an extra stage.

These next few pictures are looking top-down (without the lid). It was such a wonderful angle to photograph, I've included three pictures! I think these are some of my favorite photos that I've had the change to take recently.

Now let's have a look at the radial (rho) stage, that physically translates the magnetometer from the center of the polar circle, outward along a radial line.

Radial (rho) stage (including the magnetometer)

The radial stage definitely looks unusual, but it's what my brain settled upon after thinking of many more complicated ideas. The idea here, again, is to keep all of the moving metal parts as far away from the magnetometer as possible, while still being able to transfer precise linear motion to the magnetometer.

Looking down from the top of the stage, we can see the magnetometer itself (an HMC5883L breakout board from Sparkfun), which has to move from the center of the circle all the way to one side (the right side, in this orientation). It's mounted on a tiny linear stage, and instead of a belt or screw, it uses a cable to transfer linear motion. I've seen this before in some old pen plotters that I took apart years ago, and it really seemed to fit this niche. An elastic band (left side) provides tension to return the axis to the center when the cable isn't actively being pulled.

Kind of silly, but the string that I used at first broke after only about 100 cycles, and I needed to find something around the house that could serve as a more durable replacement. I ended up substituting in some satin dental floss, which causes the machine to smell very pleasantly minty when operating! :)

Here's the underside of the radial (rho) axis. Since this axis moves in several directions relative to the rest of the machine, and contains the sensitive magnetometer, everything is made out of nonmetalic materials. The machine screws and bushings are nylon, and the linear rails are made out of 1/4 inch delrin rods. The tiny carriage that holds the magnetometer is just four pieces of MDF sandwiched together, with press-fit slots for the bushings, captive t-slot nuts for the magnetometer to mount to, and cutouts to securely hang onto the elastic and cable, er, I mean dental floss...

The range of motion (about 4cm, currently) is so short for the radial axis, that we can get away with using a servo motor instead of a stepper, and save an extra stepper controller. This also provides reasonably accurate absolute positioning without the need for a homing endstop or external encoder.

The servo is mounted towards the bottom of this axis (which is about 20cm tall), to keep it as far away from the magnetometer as possible.

And here's the whole thing, indexed up in Z about 4cm. Time to give it a try! I connected it up to an Arduino, and wrote a quick sketch in Processing to visualize the magnetometer field strength at a given location. The Z axis still isn't perfect and has a bit of a ~5mm wobble (it will likely require a third lead screw for stabilization), so I just captured one 2D circular slice of the cylindrical volume, pictured below.

Here we have the very first rough magnetic field image from the machine! This is a baseline image, so the fields are just from Earth's field, as well as whatever the machine itself generates. The variation is surprisingly low -- dark represents the lowest measured field (about 40uT), and light represents the highest field (about 52uT). Samples were taken every 10 degrees in theta, and about every 2mm in rho, so this represents a circle that's about 6cm in diameter, and is the average of about 64 samples per point, which got the variation down to about 0.1uT, which translates into a frequency variation of only 4Hz in the frequency domain! For orientation, the lighter area is centered towards the area of the machine that has two lead screws closer together, where as the dark is centered around the single lead screw.

There's still plenty to do with this rig to characterize the measurements and determine it's accuracy, but it's certainly exciting to see some initial data from the machine.

Thanks for reading!

Let's have a look at a first pass at making a simulator for the coded field MRI.

Simulating an instrument is a helpful way to understand the design, how different elements interact, how the instrument behaves in the presence of noise, and identify any issues early on to help inform your design decisions. I have some experience with this from my first postdoc in designing an adaptive coded-aperture spectral imager, and so I've started putting together a simulator for the coded field MRI to help understand the design considerations, and what kind of performance one might expect with such a system with specific design decisions. The high-level and very powerful MATLAB numerical simulation suite is the standard tool for constructing these simulations, but in the spirit of open source I'll be using GNU Octave, an open-source effort at cloning much of MATLAB's functionality.

Some folks like to design all of the individual components of a system and then piece them all together at the end. I prefer to have a simple but modular system up and running end-to-end so that I can see how each new component affects the system, and get a better intuition of how things work. Here I've put together a very simple simulation that is idealized and doesn't yet incorporate many important physical phenomena, and so we'll progressively add them in over the course of the project as we get a better appreciation for them.

The basic questions that we might have at the beginning of this project are:

• How accurately do I have to measure the magnetic field of the code to arrive at accurate reconstructions?
• How many measurements will it take to reconstruct an image? How many different codes? (and, ultimately, how long will each slice (or volume) take to measure?)
• What is the relationship between the number of measurements and reconstruction quality?
• How does noise affect the reconstruction quality?
• How does the range of magnetic field intensities in the code field affect the number of measurements?
• How small will the magnetic resonance signal be? How sensitive would a receiver have to be to pick it up?
• What frequency range will the receiver have to be sensitive at, and what sampling rate will it have to have?

and many others. Here we'll begin to find answers to some of these.

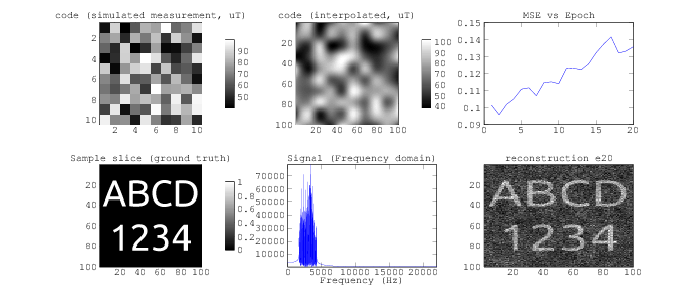
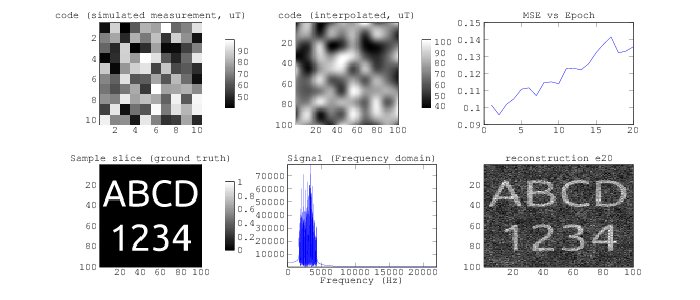
Let's orient to the simulator (above).

• Code (measured) (top left): Here we have a low-resolution simulation of the coded field, as measured from the magnetometer. This simulated code field is measured at a 10x10 resolution (to help ground this, you could think of it as 10cm x 10cm), and each "pixel" of this code is currently randomly generated to be between a certain range (say 40uT to 55uT). In practice, this will likely need to be much closer to a 1mm resolution, but it's helpful for visualizing. Random codes likely aren't physically realizable with whatever configuration of code field gradient coils we end up putting together, but random codes are popular in coded aperture imaging, so we'll start here.
• Code (interpolated) (top center): Here we make the assumption that the code intensity is slowly varying over distances that are smaller than the the measured code, and interpolate the measured code to a higher resolution to get a better map of the field intensities over our simulated sample.
• Sample (bottom left): Our simulated sample -- here just two dimensional, and a test pattern. In reality this would be the fruit, appendage, or other sample that you're trying to measure.
• Signal (bottom center): The simulated signal generated by the sample given the code field, after one magnetic resonance pulse (ie. placing the sample in a ~1T field, then quenching the field so that it quickly collapses down to the code field, and recording the signal produced). This signal is in the frequency domain.
• Reconstruction (bottom right): Our reconstruction of the sample, after a given number of measurements.

The simulator also includes a graph of the error in the reconstruction over time (top right), but I'm not sure that the metric I'm using now is well fit for this task, so we'll ignore it for now.

Before looking at some initial results, let's get an idea of the process, to help ground the ideas in the last post.

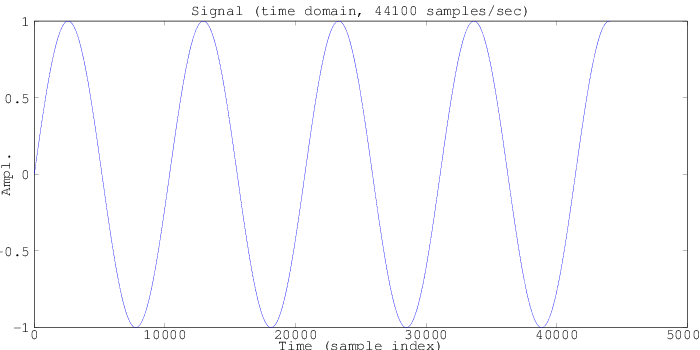
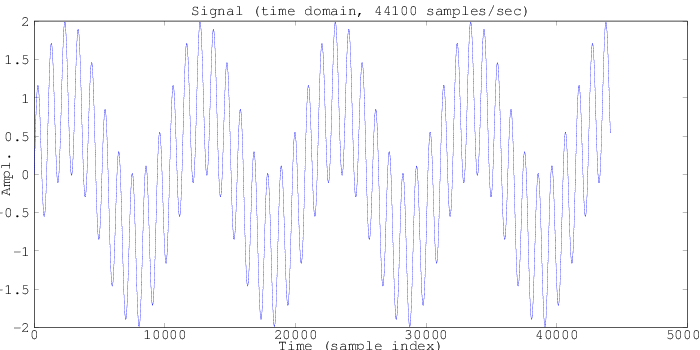
The magnetic resonance process from the proton precession magnetometer protocol causes the nuclei in a given spatial area to precess at a frequency determined by the magnetic field strength at their location. Assuming that the magnetic field strength is perfectly uniform, the signal might look something like this (above) -- a signal at one frequency. Note that physically has an exponential decay in it (the T2 relaxation), but here we're going to start with something exceedingly simple that doesn't decay, and add in a decay model later.

Now imagine instead of listening from only a single spatial location, we listen from two -- each having a different (but completely uniform) magnetic field strength. The signal might look something like this (above), with two frequencies -- one from each spatial location.

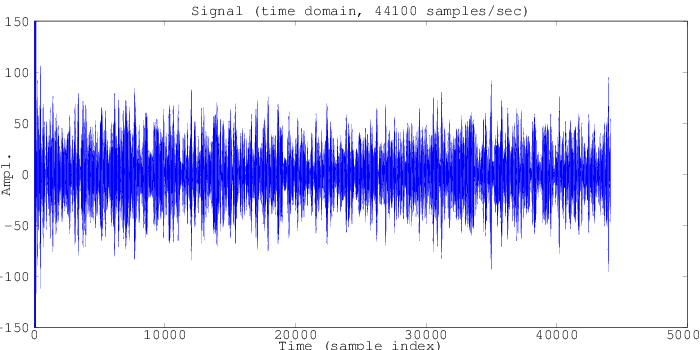
Extending this further to the 100x100 (10,000) points modeled in this simulation, we can see an absolute cacophony of 10,000 spatial locations all broadcasting their magnetic resonance signals at once. Here we'll switch to the frequency domain, where it's a little easier to make out the structure of this signal.

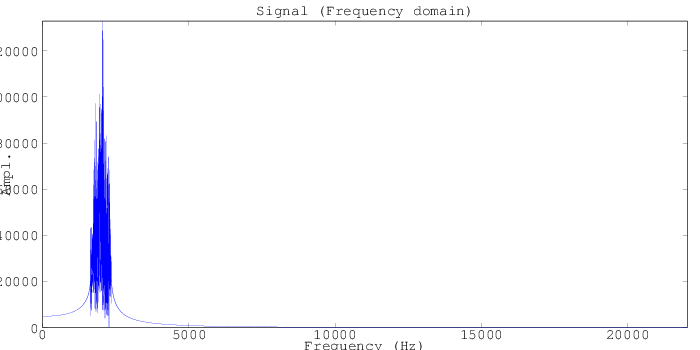
Here on the frequency domain plot we can see a large set of signals over a short band of frequencies around 2kHz, corresponding to random code intensities between 40uT and 55uT. Here, each frequency represents somewhere between one to a small number of spatial locations, and the amplitude represents the sum of the "signal" (say, the amount of water at a given location, represented by the intensity of the sample image).

Now, with a knowledge of what our code looks like, we can start to back out what the original sample looked like -- and that reconstruction will get better as we include more and more measurements with different codes.

Here's a first simulation, with the original sample (left), as well as the code (center) and reconstruction (right) as we progress from 1 to 20 measurements. At first the reconstruction is terrible, and looks very little like the sample -- but as we accumulate many measurements from different codes, the reconstruction starts to resemble the sample. This is because each code is full of ambiguities -- since the magnetic field intensity at a given spatial location could be the same as the intensity at another spatial location, the signal at a given frequency can't be accurately attributed to a given spatial location. One code might pool together spatial locations A and B into one frequency, so we can't tell how much came from A and how much came from B. But the next code might pool A and C into one frequency, and the next one A and D, and so on, and so after many measurements with many different (and known) combinations, we can start to back out what the signal from location A, and all the other locations, must look like.

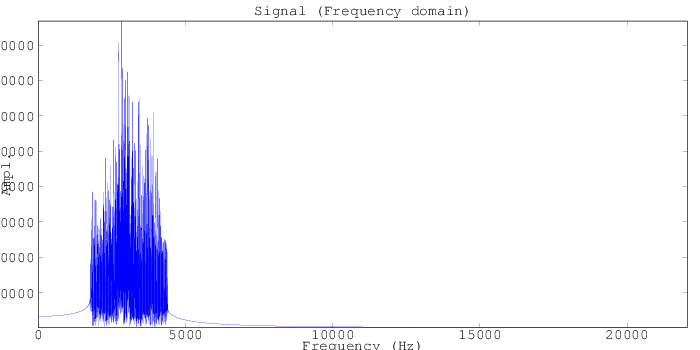
The last simulation was using only a very narrow range of magnetic field intensities in the code (40uT to 55uT), and so it had to pack a lot of information into a small band of frequencies. Let's increase the code range to between 40uT and 100uT (we're still in fridge magnet territory on these intensities), and see how this helps out our reconstruction. Above we can see that now our signal spans from between about 2kHz to 4kHz, which is still able to be well-sampled using our simulated sampling frequency of 44.1kHz (audio sampling rates).

This reconstruction definitely looks a lot better! By 20 measurements we can clearly make out this slice, although it's still a little noisy. For comparison, here are the reconstructions from the two simulations after 20 measurements:

Just for fun, I found two slices online from actual MRIs of produce, and put them into the simulator. The first is an orange with lots of signal, simulated with codes from 40uT to 150uT, out to 20 measurements. The reconstruction looks pretty good! Though the fine structure in the peel and between the orange slices would likely take many more measurements to recover.

And while the test pattern and orange have lots of simulated signal, let's try this apple, whose amplitude is much less intense in most areas. Here we simulate with codes from 40uT to 100uT, but out to 100 measurements (or 5 times longer than the other simulations). This one definitely takes longer to reconstruct, but it does an okay job with the general structure after about 30 measurements, and picks up some of the finer structure and contrasts closer to 90 measurements.

The beginnings of the simulator are starting to take shape, and while these numbers will move around a lot as the simulation becomes more accurate (particularly with the addition of noise, the properties of a radio receiver, and more physically realistic codes that include field orientation), it's encouraging to have and end-to-end system, and begin to get an appreciation for the coded field system along with some very preliminary results.

Thanks for reading!

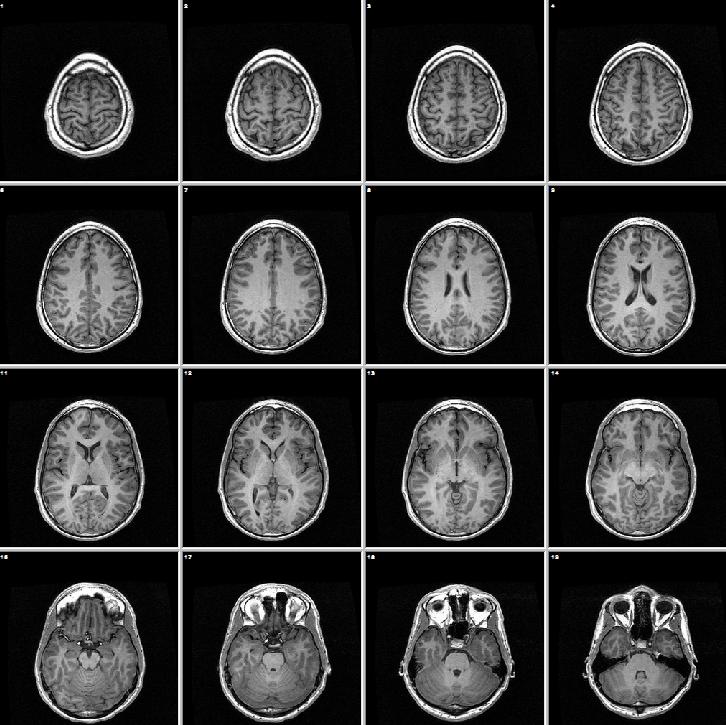
I happen to think that magnetic resonance imagers, or MRIs, are one of the most incredible machines that humans have built -- right along side spacecraft and large hadron colliders. MRIs are volumetric imagers, which means that they can scan inside objects and produce very accurate three dimensional renderings of where certain protons are, like the protons in the two hydrogen atoms that make up each water molecule.

I confess that I didn't have a full appreciation for just how incredible MRIs are before taking an Advanced Brain Imaging class in graduate school, about six or seven years ago. Before hand I was largely only familiar with the common structural images that MRIs take, like the ones of my brain (above) often for diagnostic medical imaging like locating tumors or characterizing trauma. In cognitive neuroscience, we also made use of functional magnetic resonance imaging (fMRI), which is able to help identify the brain regions that are active when someone is completing particular tasks by measuring areas where there is increased blood oxygenation (the so-called BOLD signal). But it turns out that MRIs are capable of many more incredible methods of imaging. Magnetic Resonance Angiography can map the blood vessels in the body, Diffusion Tensor Imaging (DTI) can help image the neural connections in the brain, Magnetic Resonance Spectral Imaging can measure metabolic changes in tissue, to name only a few of the incredible techniques available. Even with all these incredible techniques, the structural images are still beautiful, and I really enjoy seeing structural scans of everyday objects, like these scans of fruits.

Magnetic Resonance Imaging (MRI) and Computed Tomography (CT)

Ever since taking that Advanced Brain Imaging class I've been thinking about how one might go about constructing their own MRI. It's not an easy task (we'll see why in a moment), but first let's look at a related imaging technique -- computed tomography (or CT) scanning. CT scanners are essentially x-ray scanners that are rotated 360 degrees around an object, and using reconstruction techniques like filtered backprojection, one can back out 3D information from a large number of 2D absorption images taken at a large number of different angles around an object.

A little over a year ago I built a prototype desktop CT scanner, using a 10uCi Barium-133 radioisotope check source as a source for x-rays, and a modified extra sensitive Radiation Watch Type 5 high-energy particle detector to sense these low-energy x-rays. The first images of produce were really exciting for a first pass at a home built scanner, like the bell pepper below:

Unfortunately, these images took a good deal of time to acquire, because of the low intensity of the source. At about 90 seconds of sample time per pixel, a ~20x20 image took all night (about 10 hours) to acquire, so doing this at 1 degree increments would mean it would take an impractically long amount of time -- about 2 months -- to collect enough data for a 3D reconstruction. This is using the most intense radioisotope source that's legally allowed to be purchased, with a detector paired to be particularly sensitive to it's emissions. To speed this up you could add parallel detectors for a linear gain (ie. 10 detectors would reduce the scan time by a factor of 10, to 1 hour per slice), or increase the intensity of the source by using an x-ray tube. As a scientist it's important to be incredibly responsible, and one's health is just to precious to place in genuine danger with such things (not to mention the legal issues that undoubtedly exist). That leaves few options for CT scanning -- either find another wavelength, or decrease the source-detector distance, and construct a bank of tens of detectors to reduce the scan time to something on the order of a day. I'd thought about doing exactly this (the prototype is sitting beside me!), but really I'm at the mercy of inspiration, and what really inspires my volumetric imaging interests is the idea of figuring out a way to build an inexpensive desktop MRI.

The basics of Nuclear Magnetic Resonance (NMR)

Prefacing this by saying that I'm only an interested amateur and not an expert on MRIs or NMRs, so you'll have to forgive the vast oversimplification, but the MRI can be though of as an imaging extension to a nuclear magnetic resonance spectrometer. Nuclear magnetic resonance suggests that we can think of different nuceli as atomic-sized magnets. When in the presence of an external magnetic field, some portion of those nuclei tend to align to be in the same direction as that external magnetic field. When in this state, they become susceptible to absorbing and emitting ratio waves under certain conditions, and an NMR (and MRI) capitalizes on this by placing an object in a large magnetic field so that some portion of its nuclei will align to that field, broadcasting specific patterns of ratio waves into the sample, then listening to the radio waves that return. These radio waves can describe the atomic makeup of the sample (spectroscopy), the location of different parts of the sample (imaging), or the magnetic field intensity in the sample (magnetometry).

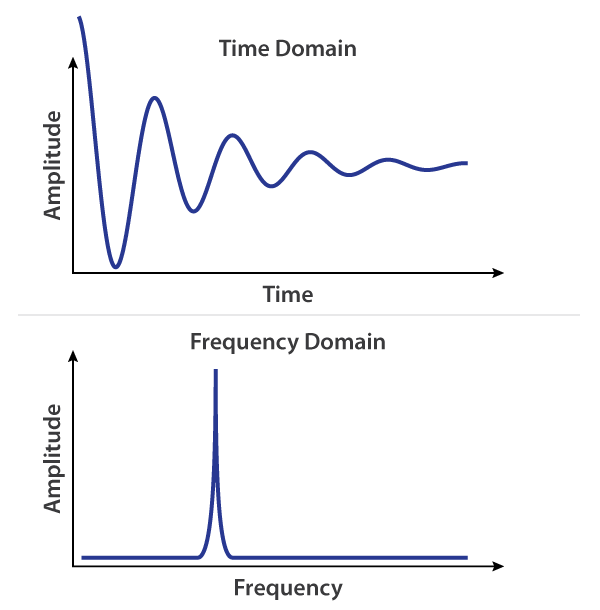
The simplest case, that I've animated below, is the Proton Precession Magnetometer (see the great PyPPM by Bradley Worley, or Signals from the Subatomic World on Amazon, for much more detailed information). Here the compass needle represents the orientation of the magnetic field of a nuclei, which starts out aligned with the orientation of a low-intensity ambient field, here the ~40 microTesla (uT) field generated by Earth's iron core. If the nuclei is then exposed to a much larger external field, say from a large electromagnet, it will shift and align it's orientation to that much larger field. If that larger field is then switched off, the nuclei will re-align to the Earth's field, slowly precessing back and forth until it has realigned to the lower field. This motion is defined by an exponentially decaying sinusoidal wave, whose frequency is defined by the Lamour Frequency, and can be picked up by an external antenna near the sample. The frequency varies with the strength of the magnetic field -- for Earth's low intensity field the frequency is only about 2kHz (audio frequencies), where as for a 1 to 3 Tesla medical MRI scanner, these frequencies are in the 40-100MHz range.

From the perspective of our receiver, we would observe the following exponentially decaying sinusoidal signal, and it's frequency, which can tell us the precise magnetic field intensity that the sample is in. The frequency variation (ie. the width of the peak in the frequency graph) can determine how homogeneous -- or how much intensity variation -- there is in the magnetic field. Traditionally, the more homogeneous the field, the more resolution one can get out of their instrument -- spectral resolution in the case of the NMR, and spatial resolution in the case of the MRI.

Because of the complexity of pulse sequences and the field homogeneity requirements, we're keeping things simple and aiming for creating (essentially) an imaging proton procession magnetometer, with a pulsed main field.

Extending NMR into an imaging technique

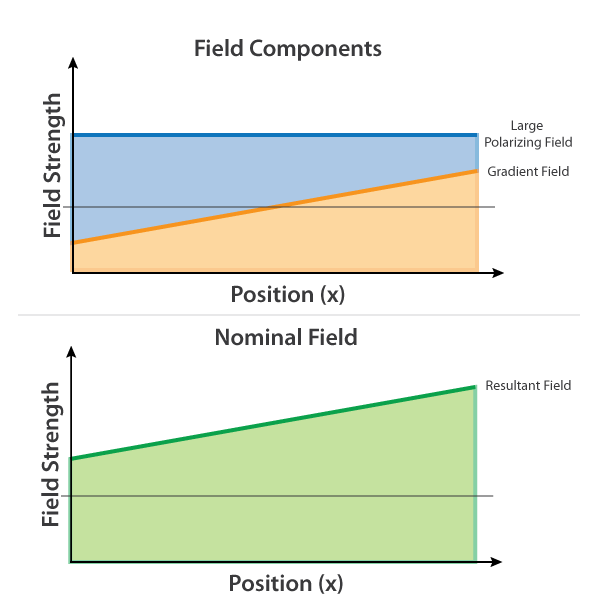
The frequency that a given sample will oscillate at depends on the intensity of the magnetic field that it's experiencing, and MRIs make use of this by introducing a slight gradient in a large main field. Where the large main field (say 1 Tesla) coming from a superconducting magnet is in blue, a much smaller gradient field (orange) emitted from a gradient coil introduces a very slight variation into the field, resulting in the sample experiencing the field in green.

Because different parts along the length of the sample experience slightly different fields, the frequency that they emit at will be of slightly different frequency. Knowing the field intensity and gradient very precisely ahead of time allows us to back out exactly what location a signal at a given frequency came from. If a large signal occurs at that frequency, we plot the pixel as (say) dark to indicate the presence of signal, and if no signal occurs, we plot it light to indicate the absence of signal.

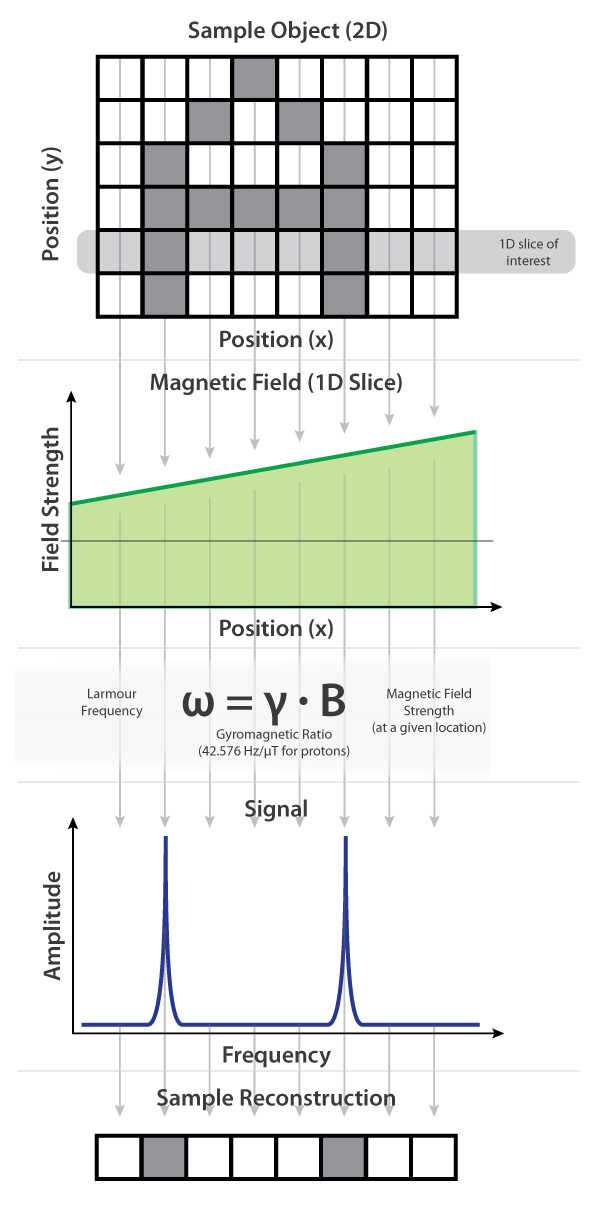
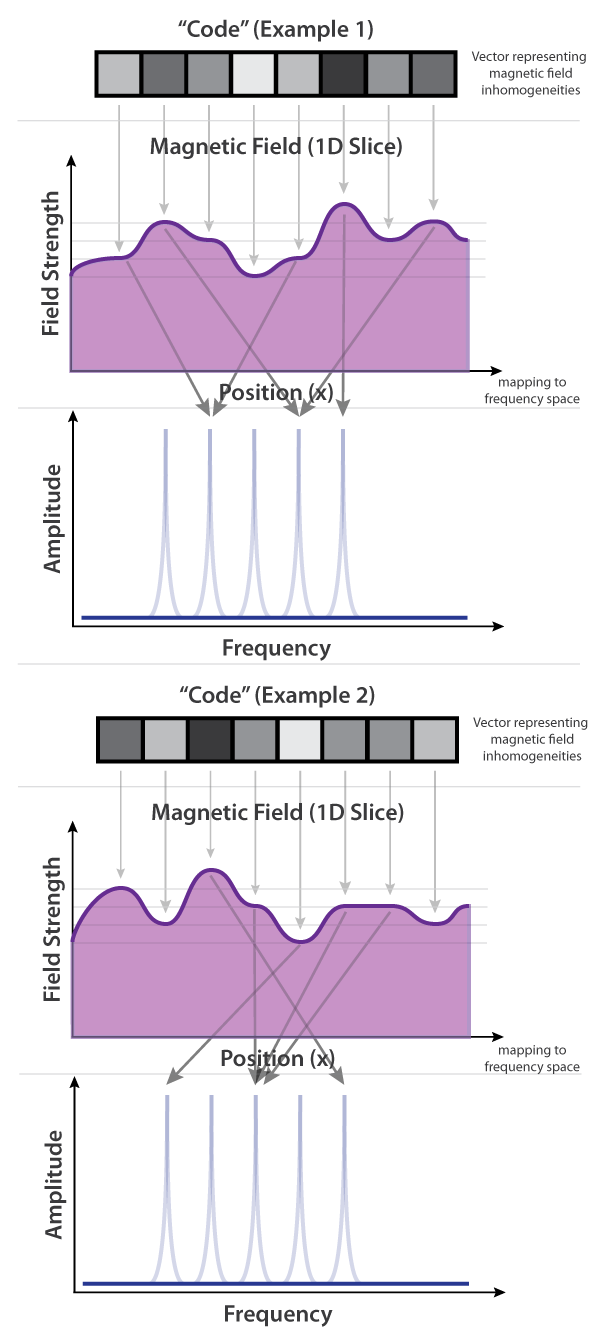
To help ground this in a 1D case, the figure below shows a single 1D slice of the letter "A" being spatially coded using a gradient field, the two locations where there is sample (x=2 and x=6) each transmitting at specific frequencies defined by the Larmour Frequency of the field intensity at their respective locations, and the reconstruction that can be generated by remapping the intensity of the signal at a given frequency back into spatial data.

Coded Aperture (or, "Coded Field")

The trouble with all of this is that superconducting magnets are fantastically expensive, and out of reach for building ones own MRI. NMRs can make use of large electromagnets that have much higher field inhomogeneities, but in order to do this they physically spin the sample around within the field so that the sample receives the "average" field intensity, but that doesn't translate well to spatial imaging.

A few years ago I did my first postdoctoral fellowship in computational sensing focusing on something called coded-aperture spectroscopy. Coded aperture spectroscopy doesn't have a good online tutorial that I can link to, but the heart of the technique is that instead of making a spectrometer that looks like a camera (where it's detector would make a high-fidelity representation of a spectrum), it places a special filter somewhere in the imaging plane so that the image on the detector looks nothing like the spectra, but the signal has been manipulated so that different kinds of inference are much easier.

In the extreme case, a linear CMOS sensor in a traditional spectrometer might be replaced with a single pixel photodetector in a coded aperture system, so that the entire spectrometer outputs only a single number per measurement cycle. At first this sounds crazy, but by changing the filter pattern on the coded aperture, you can actually target the spectrometer to do certain kinds of tasks extremely quickly (like spectral classification -- or identifying which chemicals are in a sample), and in many cases this can be done in orders of magnitude more noise than a traditional spectrometer. It's really an incredible technique.

An imaging analog to this is the Rice Single Pixel Camera, which contains only a single photodetector, but is able to take images through the use of an adaptive coded aperture. In the case of the single pixel camera (and the spectral imagers that I worked on), the coded aperture is usually implemented using a micromirror array, like those used in modern DLP projectors. By taking a variable number of measurements with different codes, one can back out what the original signal looked like, or use the signal for some specific purpose (like a spectral classification task, in the case of spectroscopy, or image identification, in the case of imaging). Surprisingly, a lot of work has been done with random codes, which work reasonably well for some tasks -- but you can also design the codes using various techniques, and this ultimately reduces the amount of measurements that you need to take for your task.

The interesting thing about considering MRI with an inhomogeneous (to a degree) electromagnet, is that it starts to conceptually look very similar to coded aperture spectroscopy and imaging. And as long as you can measure the field inhomogeneities over the sample region of the instrument (the 3D "code", in the form of magnetic field intensities and orientations) to a reasonable degree, and manipulate them, then I believe you can use the same coded aperture techniques to back out spatial data when using an electromagnet.

An example

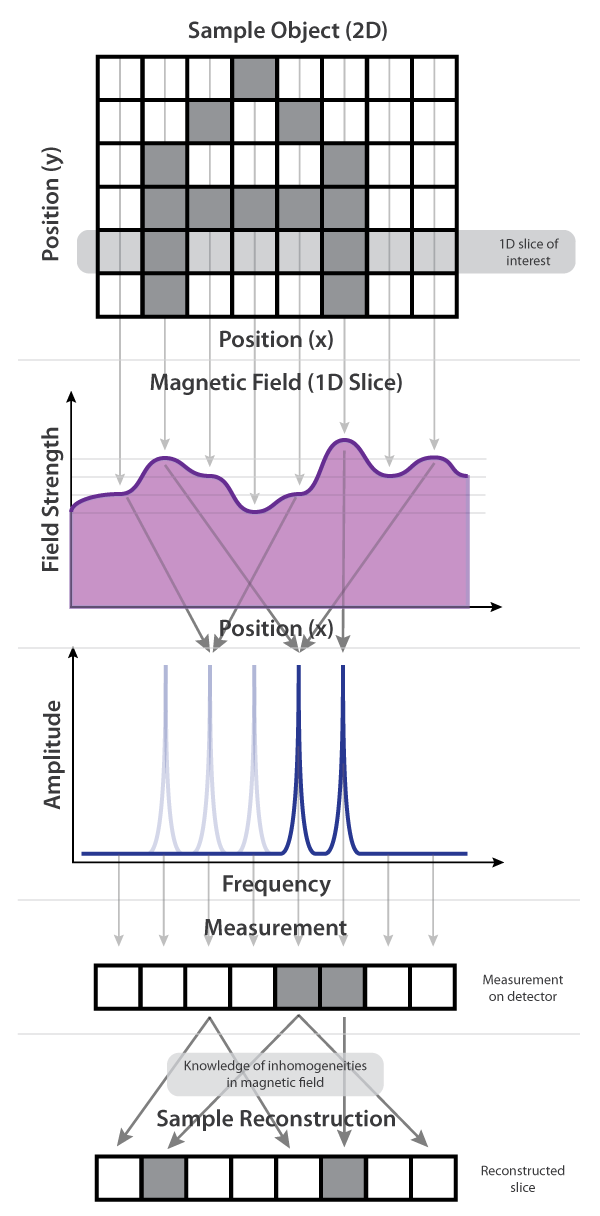
Returning to our example from above, we can substitute in an inhomogeneous but known field (purple) instead of the very precise gradient field from above (green). Now, instead of there being a linear correspondence between spatial location (x) and frequency, the mapping is more complex. In this simple example, spatial location x=1 now maps to the second frequency bin, location x=2 maps to the fourth frequency bin, and because the field intensity is the same at different locations, multiple spatial locations pool their signal into the same frequency bin. So the measurement that we take (the signal in frequency space) looks nothing like the high-fidelity representation of the slice of interest that it used to -- instead we have to add in an extra step that uses our knowledge of the field inhomogeneities (the "code") to back out what the original slice looks like.

And because multiple spatial locations may share the same frequency bin (for a given code), we have to measure the same slice using a number of different codes to properly reconstruct the original slice. Generally the more codes that are used, the more accurate the final reconstruction will be -- although instead of using random patterns on the codes, you can design the codes using different techniques to decrease the number of measurements that are needed (relative to random codes) for a given reconstruction accuracy.

Below are two examples of codes -- the first one is the same as we just saw (above), and the second one is another random code with a different spatial mapping. We can also approximately represent these codes as discretized 1D images, as below, where the field intensity of the code at a given spatial location is represented by the intensity of the pixel at that spatial location (here, darker means a more intense field).

And these are only two examples -- in practice we'll likely need tens or hundreds of different coded field configurations in order to arrive at an accurate reconstruction of the sample.

And so, the idea here is that we essentially try and trade off having an extremely homogeneous magnetic field with having an imprecise, variable, and extremely well characterized inhomogeneous field. We trade a great deal of cost for added complexity and time -- the requirement to have a "code coil" configuration in place of gradient coils, the requirement to characterize our fields (which will take a good deal of time in a calibration step prior to scanning, and will likely have to be recalibrated with some frequency), and the requirement that we have to take many more measurements to reconstruct the sample. We also won't be able to do most of the things that an MRI can do, except for structural imaging, and at a higher noise level than the million-dollar medical systems currently in use today. But the benefit, if it works and we can build it, is having an inexpensive desktop magnetic resonance imager, and even a few cubic inches of scanning volume with reasonable spatial resolution would be incredible.

Measuring magnetic fields in space (or, making a magnetic camera)

In order for this technique to work, we need to have a very good representation of the magnetic field intensity of the "code" field over the entire volume of the machine. This is an unusual problem -- normally you might want to know the field intensity and direction at a specific location (like with the magnetometers used for inertial measurement units, or compasses in phones), but aside from sprinkling iron filings on a sheet of paper, or some of that neat magnetic field film, there aren't traditionally many options -- and those are both 2D methods! Here we need to sample the entire 3D scanning volume of our field, and measure both the field intensity and direction very accurately.

When initially calibrating NMRs and MRIs, a probe with many magnetometers layed out in a specific spatial arrangement is typically used to characterizing the field. Here we essentially need something very similar, only something that's intended to be used very frequently, and something that's mounted on an x/y/z axis so that it can quickly, automatically, and accurately characterize the fields within the scanning volume.

I admit that I don't fully appreciate what that will look like yet, because it's not entirely clear what the best configuration of code/gradient coils and such will look like -- but the idea of making a magnetic camera excited me enough a few months ago that I decided to make a quick sketch (in hardware), designed this experiment board and sent it off:

The board is an 8x8 array of the popular Honeywell HMC5883L 3-axis magnetometers that are very commonly used in the maker community (and for which a breakout board is available from Sparkfun). I chose the HMC5883L because they're very small (3x3mm), have the largest range I could find (+/-8000uT), and required a minimum of external components -- enough that I could get the packing efficiency to a 1cm grid on the camera board.

The HMC5883L communicates over I2C, and one of the issues with this is that all the sensors share the same address -- so I had to add in a bank of I2C multiplexers to be able to individually address each magnetometer. The benefit to this is that the entire array can be interfaced with using only 3.3V, GND, and two I2C pins, SDA/SCL.

To initially test the design, I populated only the central 16 magnetometers in a 4x4 array, and made a plastic enclosure without any ferrous metals nearby.

The board ended up working very well, and showed that the signals could be multiplexed in this fashion. A quick Arduino and Processing sketch showed that data was coming off, but a 1 cm grid is much too tiny to see interesting features -- it needs a mechanical scanning rig to scan the board in the x, y (+/-1cm), and z (+/- many cm) to generate images at a 1mm or lower resolution.

Unfortunately the story turns south here -- my hand stenciling abilities are not fantastic, and I don't have access to a proper stencil printer. The stencils that I use from OSHStencils are fantastic for the price, but they are quick to warn that Kapton stencils may not be ideal for very small pitched footprints (like the footprints for these magnetometers). I've found that the kapton stencils have worked well enough in the past even for these parts, but I'd never tried to align a stencil and uniformly deposit paste on a 10x14cm board covered with 200 tiny pitched magnetometers and 0402 capacitors. Still, against all warnings and inflated by my success with the 4x4 version, I gave it a try.

At first glance the stenciling looked okay, but on closer inspection many of the magnetometers had too much paste, and have very small bridges under them. I manually fixed about a dozen before admitting defeat, admiring the beautiful $200 coaster, and deciding that for an initial proof-of-concept, scanning a single magnetometer will likely be fine, it will just take 64 times as long. Once we figure out the final geometry, we can design a parallel detector, and ideally design it in such a way that we can make our mistakes cheaply when assembling it.

And so, onward.

About Us

I'm Peter Jansen, a Postdoctoral Research Fellow in artificial intelligence at the University of Arizona, where I work to try to teach computers how to learn and infer with concepts and language. I have an interdisciplinary background in cognitive artificial intelligence, computational neuroscience, astrophysics, optics, sensing, and signal processing. As the founder of the Open Source Science Tricorder project and a number of other open projects, I work to further science educational outreach and ground science education through sensing.

David Lesser, pictured here tinkering with a radio astronomy setup in a tent on a beautiful day at the south pole in Antartica, is an extremely talented and creative PhD candidate in radio astronomy at the University of Arizona. David has a great deal of expertise in designing (and using) electronics, radio equipment, and other such things that involve long wavelengths. He also knows his way around a machine shop, is much less frightened of an angle grinder than I am, and was once able to snag me some duct tape from a telescope machine shop when my radiator sprung a leak on top of Kitt Peak. Not that it's been held together by duct tape since then, or anything.

We both have a good set of common making skills, combined with a bunch of specific complementary expertise in radio, electronics, machining, fabrication, computational sensing, and simulation that make me at least 20% confident that we'll be able to put this together and make it work.

Thanks for reading!