-
Identification of a damped PT2 system
04/04/2018 at 22:24 • 3 commentsIntroduction
The identification of the system parameters from a real dynamical system is often required for model control or simulations. In many cases the dynamical system is a PT2 system with the transfer function H(s).
In case of D<1 the system is underdamped and there exists a simple way to extract the parameters k, D and wn from the step-response of the system (see PT2-System Wikipedia (german)).
In case of D>1 up to now i do not have found any simple solution to do that job and this article describes a simple method to determine the two time constans T1 and T2 of the transfer function
Method to get T1 and T2 with the measured step-response
1. Capture the step-response y(t) and normalize it
Capture the step-response y(t) and normalize so that you get the step-response with an unit-step input signal (step from 0 to 1).
![]()
2. Determine steady-state gain k
You can measure the gain k in steady-state (in the example above k=2).
3. Measure t25 and t75
Measure the timestamps where the step-response y(t) reaches 25% and 75% of the steady-state value.
4. Calculate the time-constants T1 and T2
Now calculate the time-constants of the transfer function H(s) with the following method
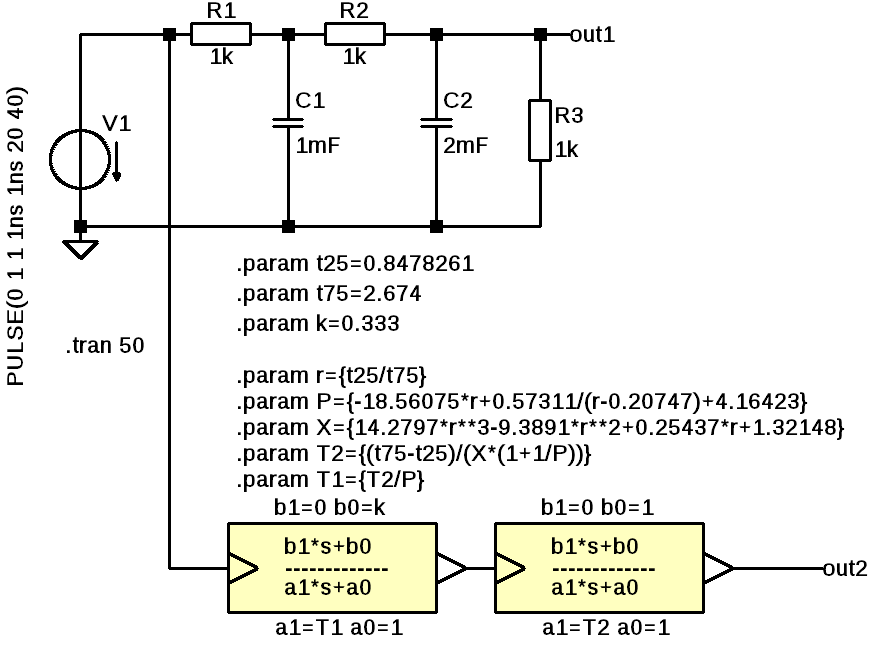
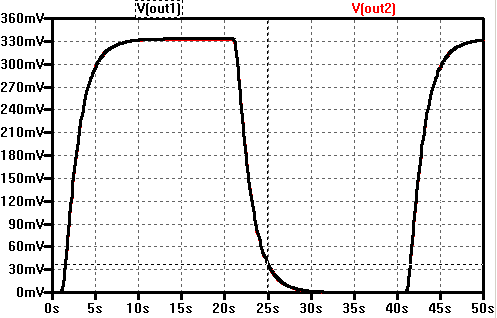
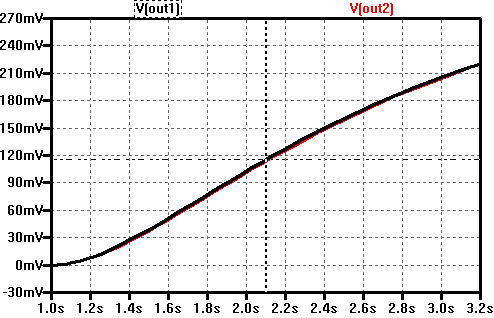
Example with ltSpice
Following example demonstrates the functionality of this approach. The step-response of a passive RC filter of 2nd order was simulated, k, t25 and t75 measured with the cursors, then T1 und T2 were calculated using ltSpice parameters and then the step-response of the analog circuit was compared with the identified transfer function H(s).
![]()
![]()
![]()
Conclusion
Many times i identified T1 and T2 of overdamped PT2 systems by fast try and error or some numerical methods. But the results were bad or it was a huge effort to get good results.
The method presented in this article allows now to determine transfer function with two simple measurements and returns the both time-constants with a high accuracy.
Feel free to test this method and give me some feedback of your experience.
I used the computer algebra system maxima to do the derivation of this equations with numerical methods (not analytical).
My Pages
Projects I Like & Follow
Share this profile
ShareBits
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
 weingaunity
weingaunity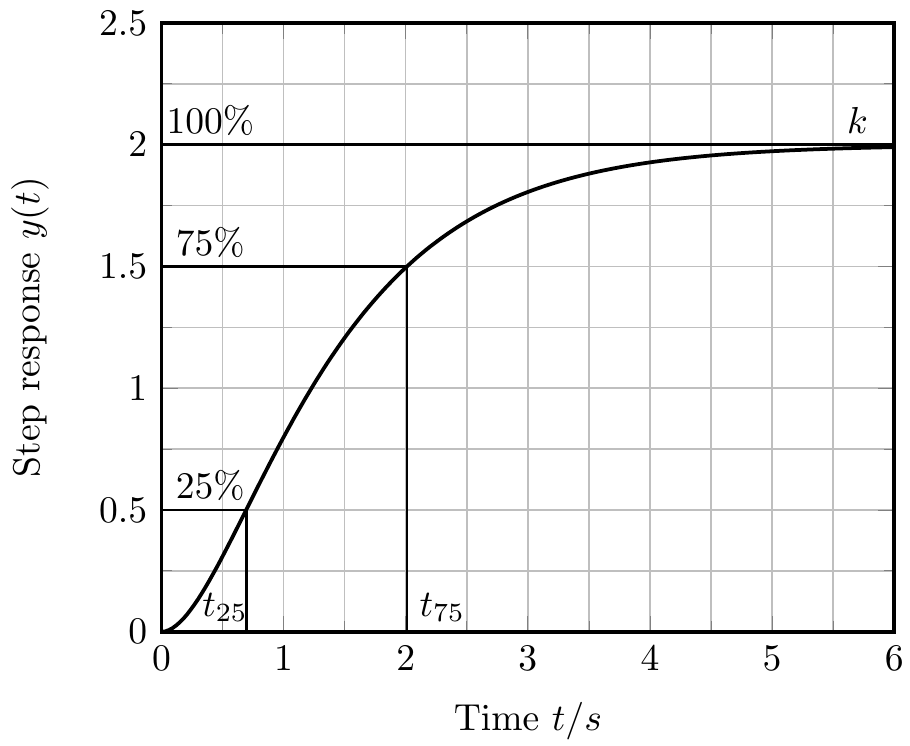
 Maarten Janssen
Maarten Janssen Chris Gervang
Chris Gervang thetazzbot
thetazzbot Arduino Enigma
Arduino Enigma CaptMcAllister
CaptMcAllister Trey German
Trey German Davor
Davor Aleksi Suomalainen
Aleksi Suomalainen Andy Lee
Andy Lee bobricius
bobricius Edgaras Art
Edgaras Art jeff
jeff shane kirkbride
shane kirkbride Kenneth Zaborny
Kenneth Zaborny martin
martin Troy Cundy
Troy Cundy Qasim Dove
Qasim Dove