Ternary Computing Menagerie

Okay, It's been a looooooong time since I added anything, but I'd like to make it up by finally publishing something that I have been working on, quite literally, for years. I have just added a file to the project that fully describes all of the ins and outs of a workable balanced ternary floating point data type. It is presented in the form of a standards document. If you've ever read an IEEE standards document, you've got the right idea.

It doesn't tell you how to build a floating point unit or library, it tells you what a floating point unit or library would need to do. That might not seem like much, but it encompasses a level of detail that required years of work and many revisions to perfect (fingers crossed). The document says version 3.1, (two major re-designs before publishing it) but I was taking notes, doing research and generally sorting out the basics long before version 1 of the document.

Anyways, it's finally done and I'm rather proud of it. I've already got some basic proof of concept work done on an FPU (very preliminary) and I'm sure I'll publish that stuff somewhere along the line.

I'm just about finished with floating point for a while. Instead I think I'll develop some work I started a long while back on a balanced ternary algebra. I'd kind of like to have a fully developed algebra that could be used to work out minimization of truth tables. In other words, using math alone to determine the most efficient hardware design to achieve a specified truth table. I already have a good chunk of it, but I think I'm still missing some basic axiom. We'll see how it goes.

I’ve experimented a bit more with parity checking balanced ternary values. As mentioned in an earlier post, the behavior is quite similar to binary parity checking. But the fact that each trit is capable of arriving incorrectly in two different ways (either incremented or decremented) causes some interesting effects.

Let’s say that a 9-trit word is transmitted, along with a single parity trit. This gives us 10 trits on the receiving end. We’ll call the original 9 trits ‘data trits’, the transmitted parity trit is the ‘parity trit’ and the calculated check trit on the receiving side will be called the ‘check trit’. If all 10 transmitted trits are received without any alteration, the check trit will be a 0. If one of the data trits is incremented, the check trit is a +. If one of the data trits is decremented, then the check trit is a -. However, if the parity trit itself is altered during transmission, the result is the opposite. If the parity trit is incremented, the check trit is a -. If the parity trit is decremented, the check trit is a +.

This phenomena is interesting, but not useful by itself since you don’t know which type of error caused the check trit to be non-zero. It may be of use in arrangements using multiple parity trits such as SECDED (Single Error Correction, Double Error Detection) schemes.

Huffman Encoding (and decoding) is very commonly used compression algorithm. It is often used in conjunction with other compression techniques but can also be used by itself. The idea is to count up each time a digit pattern (such as a bytes, 16-bit words, 32-bit words, etc.) appears in a file and then rank each pattern by how common it is. For example, if you had a file where the byte 01001100 appeared more frequently than 01001111, then the first would have a higher “score”.

After ranking the digit patterns, you assign the most commonly used bytes (or words, Unicode values, etc.) a short code-word and you assign the least commonly used bytes longer code-words. Because the bytes are being assigned code-words of differing length, this is called a variable-length encoding algorithm. The result of applying the Huffman algorithm to a file can be stored as a binary tree to aid in decoding.

The decoder on the receiving end will not know where a code-word begins or ends. To handle this, the assignment of code-words must adhere to a rule known as the prefix property. This means that no code-word may appear as the prefix to another code-word. For example: If a byte is assigned the code-word “0”, then no other code-word can begin with “0” since the first one would be the prefix of it. If a byte were assigned the code-word “110”, then “11001” would be an invalid code-word because it is prefixed by “110”, but “101100” would be valid since “110” is contained inside, not at the beginning. Sharing prefixes is okay, such as “1110” and “1111”. Both start with “111”, but as long as “111” isn’t itself a code-word the prefix property is not violated.

To adapt this to a balanced ternary system, we would use a ternary tree rather than a binary tree. There is also one additional step that is not necessary in a binary tree. Just before starting the tree you must check to see if the number of items is odd or even. More on this later.

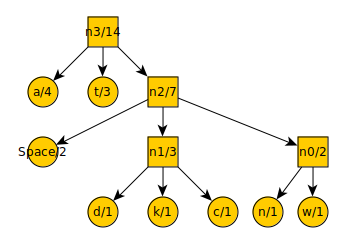
Let’s assume you are encoding a plain text file with the words “attack at dawn.” and want to compress it based on letter frequency. First, count up the letters, spaces, and punctuation:

a = 4

t = 3

c = 1

k = 1

space = 2

d = 1

w = 1

n = 1

period = 1

Then arrange them from least to greatest:

period = 1

n = 1

w = 1

d = 1

k = 1

c = 1

space = 2

t = 3

a = 4

Now is where you would check to see if the number of items is even or odd. There are nine items making it odd. In this case, the next step is to remove three items from the list and begin the tree from the bottom up. However, if the number of items on the list was even, you would only remove two items from the list. This is only done the first time when you are beginning the tree. Every other time you remove items from the list and add them to the tree, you do so in sets of three.

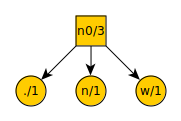
The number of items is odd, so remove the three lowest valued items from the list. There are several options that are equally low, so lets arbitrarily pick period, n, and w. These become leaf nodes with a new node above them. Each node is denoted with what symbol it represents and its frequency in the text being compressed. We then add the new node n0 to the list.

Our list now looks like this:

d = 1

k = 1

c = 1

space = 2

n0 = 3

t = 3

a = 4

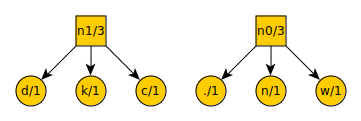
We repeat the procedure of removing the three lowest value items from the list, placing a new node over them, and putting the new node on the list. Our ternary tree now looks like this:

And our new list looks like this:

space = 2

n0 = 3

n1 = 3

t = 3

a = 4

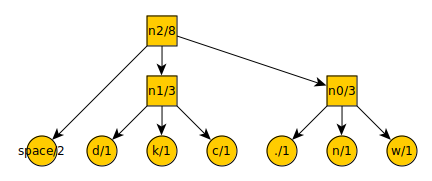
After another iteration…

The list now contains:

t = 3

a = 4

n2 = 8

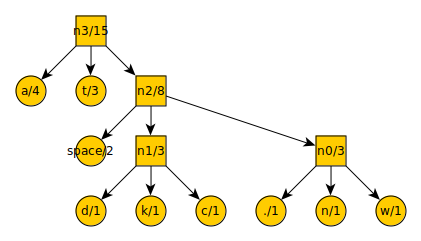
And finally:

By starting at the top, you can count every leftward motion as a -, each downward motion as a 0, and each rightward motion as a +. This gives you the code-word for each symbol. The symbol “a” is encoded into the code-word “-”. The symbol “n” is encoded into the code-word “++0”.

Let’s say that the message had been “Attack at dawn”. The period at the end is omitted, so now there are an even number of items on the list:

n = 1

w = 1

d = 1

k = 1

c = 1

space = 2

t = 3

a = 4

We would only remove two items from the list, place a new node over them, and add that node to the list. Here is the tree:

And here is the new list:

d = 1

k = 1

c = 1

n0 = 2

space = 2

t = 3

a = 4

Notice that n0 has a value of only 2 in this instance. In the previous example it had a value of 3.

We now remove the three lowest value items from the list (the removal of two items is only done the first time). Here is the tree:

And here is the new list:

n0 = 2

space = 2

n1 = 3

t = 3

a = 4

The tree after another iteration:

And the new list:

t = 3

a = 4

n2 = 7

Remove the final items from the list and add them to the tree:

If we assume that each letter took 6 trits (which is just a bit more data than 8 binary digits), the total message would have been 84 trits long. The new compressed message reads as: -00-+++++0+--0+-++--++0++-. This is only 26 trits, a savings of 31%. If the difference between letter frequencies had been more pronounced, the savings would be greater.

To decode, the sender only needs to provide the encoded message and the ternary tree data structure. With these, the decoding program can correctly recover the original message by taking the trit-stream and following it down the tree. Every time it hits a leaf node, it returns the value stored in that node and starts over at the root node with the rest of the trit-stream.

Because the ternary tree has to be provided along with the compressed message, you lose a little bit of your savings to the space taken up by the tree data structure. However, this does not necessarily need to be the case. If the sender and receiver have previously agreed on a ternary tree in advance, based on prior knowledge about which symbols are likely to be common then the tree doesn’t need to be sent. Unfortunately, it also means that the tree won’t be perfect for any given message and therefore optimal compression won’t be achieved.

In the final analysis, there is little difference between binary and balanced ternary in how the algorithm behaves. Nevertheless, it was good to sort out little details like the necessary check for evenness or oddness.

 When data is transmitted along a bus, serial interface, RF link, etc. it is common practice to do some form of error checking and correcting. This is also true of data being stored such as in RAM or in non-volatile storage. The simplest of these techniques is called parity checking and it simply detects if a transmission error has occurred, but cannot correct a detected error. Further, the commonplace implementation can only detect one incorrect bit for a given set of bits transmitted. If there is more than one error in a given set of bits, it may or may not detect the errors.

In binary systems this is normally done by XOR’ing each pair of bits and then XOR’ing those bits, and so on until you have one bit at the end. This results in a bit that is a 1 if there is an odd number of 1’s in the group and 0 if there is an even number of 1’s. This is called odd parity. If you want an even parity bit, just change the last XOR into an XNOR.

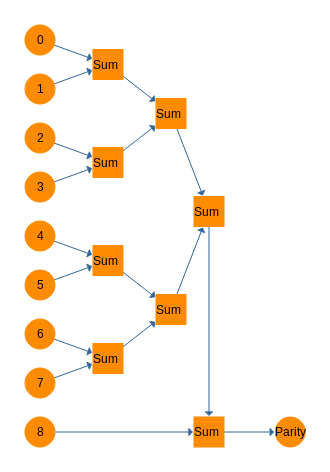
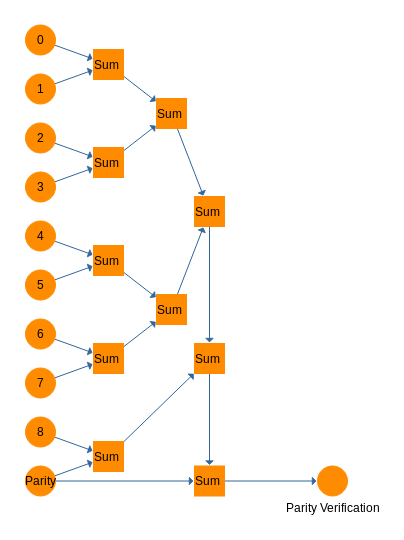
In balanced ternary, the Sum gate performs this function admirably, though the behavior of the parity trit is different. Simply cascade all of the input bits through a series of Sum gates and you end up with a parity trit. On the receiving side, do the exact same thing with all of the trits including the parity trit. Use the output of the Sum cascades and sum that with the incoming parity trit again. If this circuit outputs a 0, no errors were detected. If it outputs a - or a +, an error has been detected. Below is a diagram for a parity calculator and then a parity checker.

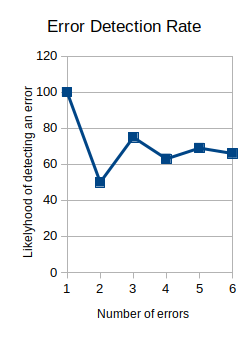
This subject brings up some interesting ideas regarding ternary errors and error correction. Consider that each trit can be wrong in two different ways instead of just one as in a binary system. Also, the parity trit can transmit data about the nature of the error by being either - or +. I haven't explored that yet, but it looks like it would be a valuable thing to know. Finally, a very interesting phenomena related to multi-trit errors. In the above ternary system, the ternary parity trit has a variable likelihood of detecting a multi-trit error. As the number of errors increases, the likelihood of detecting them oscillates up and down, narrowing each time until it finally converges on 66% or 2/3rds. I'm not sure it's useful, but it's interesting.

In this post I will describe what I consider the most important thing I've learned about balanced ternary computing thus far. A fast balanced ternary adder/subtracter.

Thus far, my research has not turned up anybody who has designed a balanced ternary adder other than the ripple-carry variety. This is fine for demonstration or testing of higher level functions, but the lack of a *fast* adder/subtracter was a total deal-breaker in terms of making balanced ternary anything other than an interesting curiosity. A ripple-carry adder has a time complexity of O(n) while a carry-lookahead adder is O(log n).

As near as I can tell, nobody has figured out how to build a balanced ternary carry-lookahead adder, meaning that we were stuck with ripple-carry adders; essentially the stone-age. I spent months of my free time bashing my head against this problem because I knew that the lack of of an O(log n) or better adder unit meant there was no point in doing any other research on the subject. Dr. Jones at the University of Iowa did figure out a carry-lookahead adder for unbalanced ternary (0,1,2) but his efforts to work one out for balanced ternary did not result in a functional design (though his work did clarify the problem quite a bit).

Ultimately, I gave up on carry-lookahead and focused my attention on a lesser-known design, the carry-select adder. A carry-select adder works by computing each possible carry-out simultaneously and passing these “carry candidates” to a multiplexer. The incoming carry from the previous digit “selects” the appropriate multiplexer input to pass along. Because the possible carry-outs from every bit position are calculated and ready before the carry-in from the previous digit arrives, each additional digit only adds a single gate delay due to the multiplexer. This type of adder has O(log n) time complexity, but takes more logic gates to build than a carry-lookahead does. These digits are put into groups with each group taking a carry-in and producing a final carry-out for the group. That group carry-out is passed on to the next group.

In a binary system, the carry-select adder requires two separate sets of logic to calculate the two possible carry candidates and the two possible sum candidates. Add two multiplexers to this and the circuit for each digit ends up being around twice the number of gates as a ripple-carry adder would need. In a ternary system, there are three possible carry candidates and three possible sum candidates, making a carry-select adder around three times size of a balanced ternary ripple-carry adder. Fortunately there are some tricks that can be used to reduce this a bit, but the end result is still pretty big.

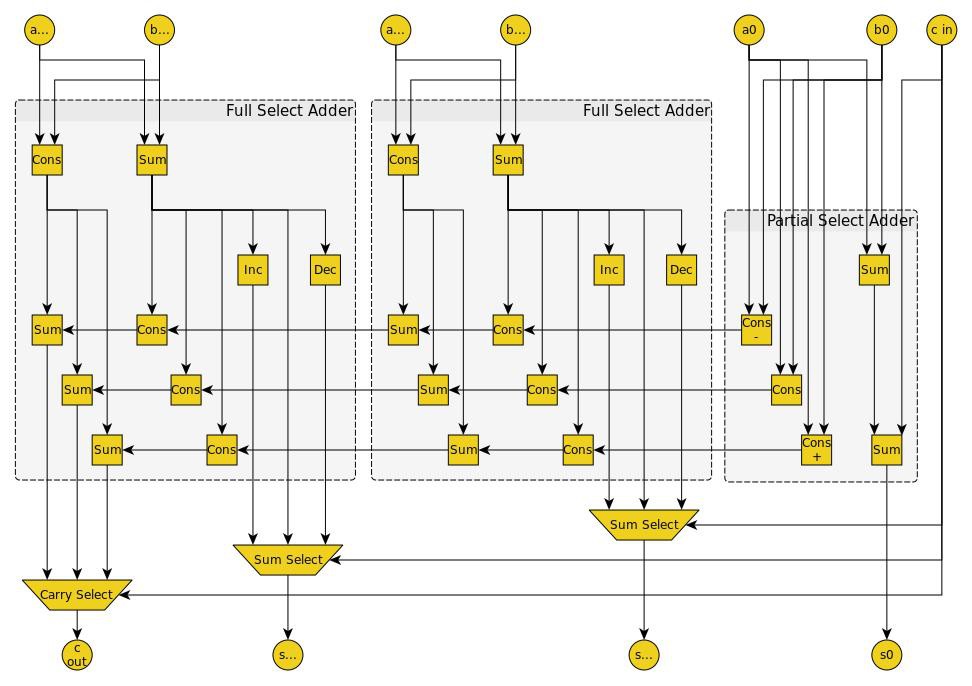
My balanced ternary carry-select adder is composed of two types of adder circuits. They are the partial select adder and the full select adder. Each group is composed of one partial select adder in the least significant position and as many full select adders as needed to fill out the group.

As you can see below, the partial select adder takes a carry-in and produces a sum and three carry candidates. No multiplexer is required in the partial select adder. A full select adder takes three carry candidates and produces three sum candidates and three more carry candidates. It passes the sum candidates to a multiplexer. Any full select adder that is not in the most significant position of the group passes its three carry candidates to the next full select adder. If it is in the most significant position, it passes the carry candidates to a multiplexer. All multiplexers in the group are selected by the single carry-in for the group.

The only gates used in these adder units are sum, consensus, increment, decrement, multiplexers, and two new ones, the minus consensus, and plus consensus. The minus consensus can be created by passing the output of a consensus gate through a monadic C gate(-00), and the plus consensus by passing the output through an R gate (00+). There may be simpler ways to make them, but that works.

As a note on gate-delays; I am just working out a rough count of delays. Obviously some gates require the signal pass through more transistors than other gates so the time to propagate a signal is not identical from gate to gate. Those kinds of details and the trade-offs between space complexity vs. time complexity vs. power consumption vs… are better left to the implementation at the silicon layer. For my purposes, I’m just interested in getting a O(log n) adder/subtracter design that works.

If you count it out, the above three-trit carry-select group has six gate-delays from the first set of carry candidates in the partial select adder, to the final carry-select multiplexer at the end. However, the carry-in is already at the carry-select multiplexer and waiting for the group carry-out candidates to propagate down to it. This is the key to why the carry-select adder is faster than O(n).

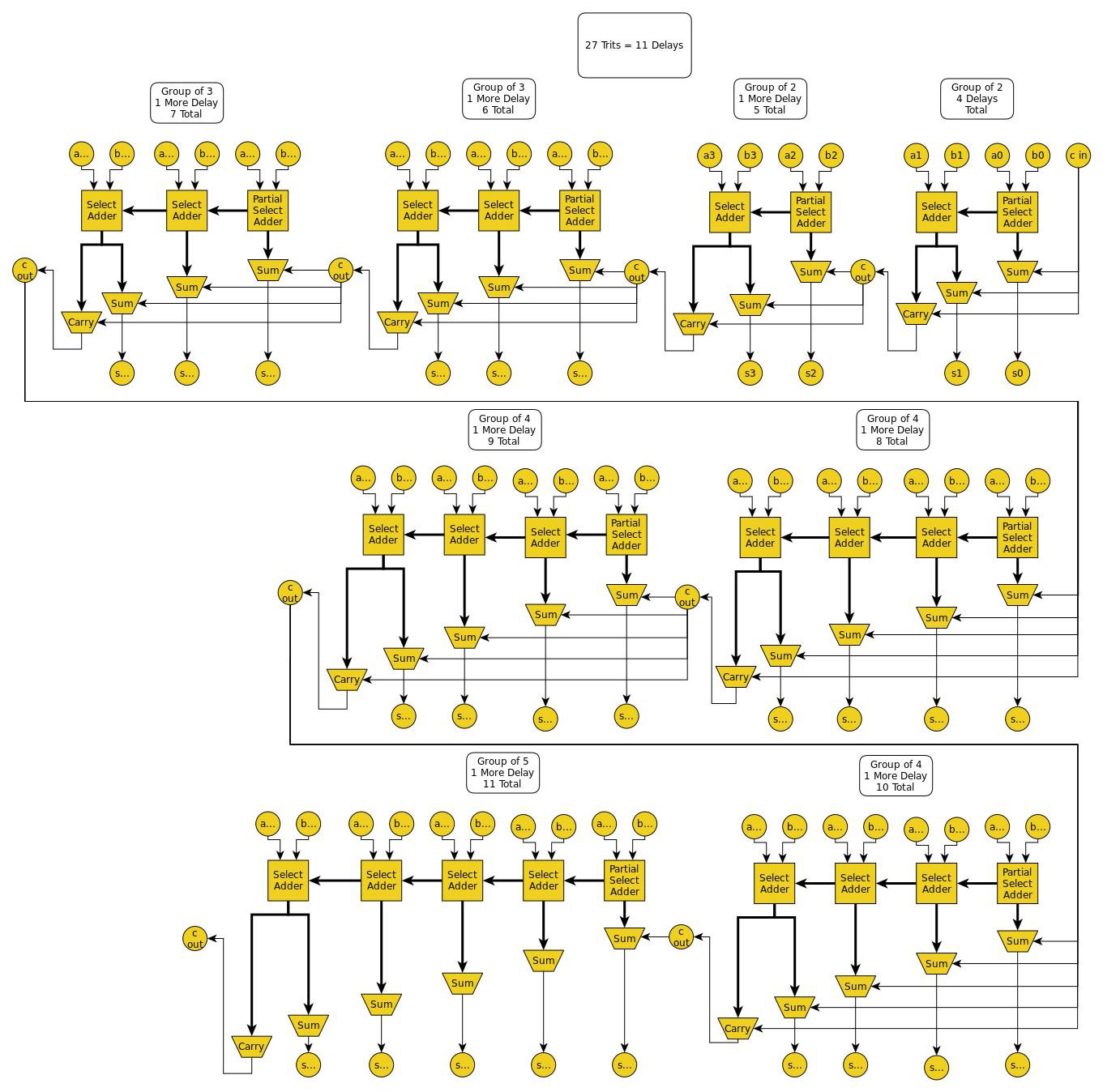
Following is a 27-trit carry-select adder that takes advantage of that to compute 27-trits with only 11 gate-delays. Each group is calculating its internal sum candidates and carry candidates and getting them ready just in time for the carry from the previous group to arrive and select the correct candidates.

Voila!

Balanced ternary shift operations have different results than binary shift operations for four reasons:
1) The value of each digit position is a power of three rather than a power of two.
2) The values that can be shifted out could be a -1, 0, or 1 instead of just a 0 or 1.
3) All balanced ternary numbers are signed (except 0, technically).
4) The sign trit is not necessarily the most significant trit of the number. Thus, both left shifts and right shifts may or may not alter the sign of the number.

On most binary architectures there are three shift operations and four circular shifts. The three ordinary shifts are the right logical shift, the right arithmetic shift, and the left shift.

In a left shift, each bit is shifted one position to the left. A zero take the place of the least significant bit and the most significant bit is lost. In some cases the MSB may be preserved in the carry flag of the status register.

A right logical shift is the same operation, but the shift is to the right. A zero takes the place of the most significant bit and the least significant bit is lost. It is proper to use for unsigned numbers. In most cases the LSB is not preserved in the carry flag of the status register.

A right arithmetic shift is a little different in that the least significant trit is lost, but the new most significant trit is copied over from the existing most significant trit so that it does not change. This is so that the sign of a signed number remains the same after a right shift. In some cases the LSB may be preserved in the carry flag of the status register.

In balanced ternary, a left shift is a multiplication by three just as long as the trit shifted out is a 0. If a non-zero value is shifted out then it is not a straight multiplication and the sign will have changed unless the new most significant trit is of the same value as the one that was lost.

There is no distinction between a right shift and a right arithmetic shift. They are the same thing because the sign of the number is dependent only on the most significant non-zero trit. By shifting in a 0, the sign of the number is automatically preserved. The exception is if the shift drops off the only non-zero trit at which point the overall value becomes zero.

A right shift is the equivalent of dividing the original value by three and rounding toward 0. If the trit shifted out was a 0, then the value was perfectly divided by three without rounding. Rounding toward zero means that if a - was shifted out, the number is rounded up toward 0, but if a + was shifted out, the number is rounded down toward 0. In balanced ternary, rounding always approaches zero, not +infinity or -infinity. In contrast, binary rounding always trends toward -infinity.

The circular shifts take the bit or trit that was shifted out and make that the value that gets shifted in on the opposite side. They have two directions, left and right, and two variants, with carry and without. The rotate-through-carry simply treats the carry-in digit as if it were the least significant digit, so the total length is word-length + 1.

There is no functional difference between binary and balanced ternary when it comes to circular shifts.

I've been working on the subject of ternary logic and ternary processing for years on and off, but I haven't been doing so in such a methodical way as I am now. By approaching this in a more methodical and comprehensive way, I have discovered a rather a big error in my logic.

Until now, I've been assuming that with careful design, a balanced ternary system could be made that would still be code-compatible with a conventional computer. Of course I knew that the internals of the compiler would have to have some significant work done to both interpret new syntax and to target a new (and highly unusual) architecture. Nonetheless, I was sure that existing code could somehow be shoe-horned in to the new system. This looked hopeful right up until I started trying to incorporate bitwise operators into the running thought-experiment I've been writing up in these posts. I didn't notice the problem when going over the NOT operator earlier and I started to get a hint of it when trying to get bool's and kleene's to play nice together. I finally realized the scope of the problem when I got into bitwise AND, OR, and XOR.

Each operator is useful for a variety of different purposes because of how they manipulate the bit pattern of their operands. But in a ternary system, the operands themselves are ternary, so even if you kept the operators identical, they will come up with unexpected answers every time. Basically, anything that is expecting to work at the bit-level will be broken. Anything that expects to work at the register/word level or that has to do with control flow, can be made to work.

So, going back to the beginning with bit-level subjects:

1) bools should still exist. To follow logical expectations in a balanced ternary environment, their FALSE representation should be a -, not a 0. I still favor strict value-checking so that bools can only hold a - or a +, nothing else.

2) Bitwise NOT and tritwise NEG (negation) become the same operation. NEG switches -'s into +'s and vice versa but leaves 0's alone. Since bool's now use - for their FALSE condition and + for their TRUE condition, there would be no difference between NEG and NOT when using them on bools or kleenes. However, NOT would produce unexpected results if applied as a bitwise operator to other types of data, just like bitwise AND, OR, and XOR would.

3) The other bitwise operators such as AND, OR, XOR, and the various shifts, would have utterly different effects than they would in a binary system. The solution is not to try to force them into the system. The solution is to find equivalent tritwise operators that produce the results that programmers want out of the conventional bitwise operators.

4) This doesn't effect logical operations or arithmetic operations. Those are just fine as previously described.

I don't have a comprehensive list of which ternary operations would produce each of the results people are currently using bitwise operators for (except NEG of course). There are 19,683 different possible tritwise operators (not counting shifts), so that would be a job about 1,200 times more complex than coming up with everything in the "Hackers Delight" book from scratch and then writing a book about it.

Instead I'll write up the few I know of right now, and then as I find them or learn of them, I will do a separate post on any new "tritwise operator candidates". I say "candidates" because choosing which operators to implement in a real processor will be an important point. Digit-level operations generally take place directly inside the ALU, which means that independent circuitry has to exist in the ALU for every digit-level operator the processor is capable of executing. To avoid unnecessary complexity in the ALU it will be necessary to carefully choose which operations to include. Of course, any tritwise operations that are also necessary for arithmetic will be there anyways, so you get those "for free". The exception is the shift operations. Those are often done in a separate piece of hardware from the ALU. I'll look into shift operations in a separate post.

One other important factor to note is that not all of the two-input gates are symmetrical and could produce different results if the input and the mask are switched. In the below examples I am assuming that the mask is always input 'a' and the data being masked is always input 'b'. If both arrangements are useful it could be arranged to get an extra tritwise operator without any additional hardware in the ALU. It also means that if you were applying an asymmetric operator to two variables (instead of masking) then a <operation> b would produce different results than b <operation> a.

Free tritwise operators used in basic arithmetic. They may have other uses I haven't thought of yet:

Negation gate (5)

A Single-input gate, negations performs an inversion on a single trit by switching -'s and +'s. Also used in performing subtraction. However, it may not be needed as inversion can also be performed by the XNOR gate below by masking with all -'s.

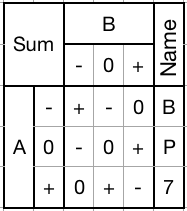
Sum gate (BP7):

Performs single-trit addition by returning the sum of two trits. Also used in multi-trit addition, subtraction, and probably multiplication.
1) Mask with a - to decrement the input trit.
2) Mask with a 0 to pass the input trit through unchanged.
3) Mask with a + to increment the input trit.
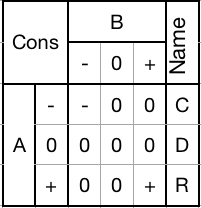
Can be used to selectively increment, decrement, or pass through any trit.

Consensus gate (CDR):

Calculates the carry-out of an addition or subtraction. Returns - if both inputs are -, returns + if both inputs are +, otherwise returns 0.
1) Mask with a - to pass through only -'s. Anything else becomes a 0.
2) Mask with a 0 to set the trit to 0.
3) Mask with a + to pass through only +'s. Anything else becomes a 0.
Can be used to selectively detect -'s or +'s, or to neutralize any trit.

XNOR gate (5DP):

Performs single-trit multiplication. Almost certainly going to be needed for multi-trit multiplication.

1) Mask with a - to invert the input trit.
2) Mask with a 0 to set the trit to 0.
3) Mask with a + to pass the input trit through unchanged.
Can be used to selectively invert, neutralize, or pass through any trit.

So far I've identified four other operators that have a clear use and could be candidates for inclusion in a processor. Below are the names, truth tables, and how they can be used. They may have other uses I haven't thought of.

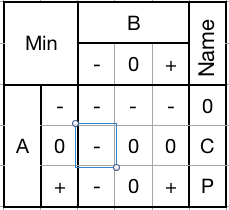
Min Gate (0CP):

Passes through the lessor of each input trit. Equivalent to an AND gate.
1) Mask with a - to set a trit to -.
2) Mask with a 0 to clamp +'s down to 0's.
3) Mask with a + to pass an input trit through unchanged.
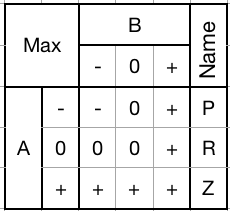
Can be used to selectively clamp down, pass through, or set any trit to -.

Max Gate (PRZ):

Passes through the greater of each input trit. Equivalent to an OR gate.
1) Mask with a - to pass an input trit through unchanged.
2) Mask with a 0 to clamp -'s up to 0's.
3) Mask with a + to set a trit to +.
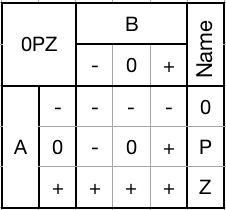
Can be used to selectively clamp up, pass through, or set any trit to +.

0PZ gate:

Several of these gates are probably going to be used in the status register for detecting the most significant non-zero trit.

1) Mask with a - to set a trit to -.
2) Mask with a 0 to pass an input trit through unchanged.
3) Mask with a + to set a trit to +.
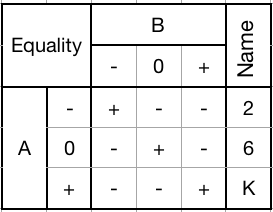
Can be used to selectively set any trit to -, or +, or pass them through unchanged.

Equality gate (26K):

Mask with a desired pattern of trits. Every trit that matches the pattern will be set to +. Any trit that doesn't match will be set to -.

Much more research will need to be done to see what logic and math tricks can be performed with these gates and which other gates would be of equal or greater value in the ALU.

Control statements such as While loops, Do-While loops, For loops, Switch statements and If statements are most of the reason you have relational or logical operations in the first place. Looking at how balanced ternary values fit into this system of program flow is of the highest importance.

To put it simply, the existing control flow statements should work the same as always. Nothing would stop you from using kleene data types or the spaceship operator for the decision making, but it doesn't actually change the way the statements work.

If variables a and b are kleenes, then:

while ((a <=> b) >= NEUT)...

is equivalent to:

while ((a >= b))...

No new ground is being broken here, they would just work as you would normally expect them to. Of course existing control statements are expecting boolean evaluation so they would need to do type checking to correctly handle kleene FALSE because it would look like a boolean TRUE due to being non-zero.

All this doesn't mean that control statements that take advantage of the more expressive ternary logic couldn't be created. An alternative to the "if" statement is easy to work out.

Imagine a conveyor belt that could be moving forward, moving backward, or stopped. The variable that held the current conveyor motion is a kleene called "conveyorDirection" that contains a - (FALSE) for reverse, a 0 (NEUT) for stopped, or a + (TRUE) for forward. Now imagine a control statement that natively evaluated kleenes. We'll call it an evaluation statement or "eval" statement.

eval(conveyorDirection)
{
     //Code if -
}
{
     //Code if 0
}
{
     //Code if +
}

The syntax could be different as long as it was clear which section of code would be executed for each state.

This could even be used to ease debugging and error handling. Imagine you were evaluating a game variable called lifePoints. This variable should never be negative. In a boolean system, if an off-by-one bug or manipulation resulted in underflow, the negative non-zero value would return TRUE, so additional steps would have to be taken to check for this. With this hypothetical eval statement you have a convenient place to put your error handler call or even a breakpoint for your debugger.

eval(lifePoints <=> 0)
{
     //Code if -
     invalidValueHandler();
     //Feel free to put breakpoint here as well
}
{
     //Code if 0
     printf("You Died!");
}
{
     //Code if +
     printf("%d remaining", lifePoints);
}

An alternative while loop is a bit more complex. Currently, while loops test an expression and if it returns TRUE, executes the code, then tests the expression again, and so on. Any combination of TRUE, NEUT, and FALSE could be manipulated with conditional operators to evaluate TRUE, so the while loop (and do-while loop by extension) can already handle any three-value expression you want to throw at it.

A natively ternary version of the while loop might be something that evaluates an expression and then chooses which code to loop through. Let's call this hypothetical control statement a "choice loop". The distinguishing feature is that it will switch back and forth through different loops (scary, right?) depending on the return value of the expression. If it returns FALSE, one section of code is looped through until it returns something else at which point it loops through that code, and so on. A break in one of the sections would release the loop. Here's an example.

choice(x <=> 0)
{
     //Loop if +
     doSomethingRepeatedly...
     x--                         //This loop executes repeatedly and decrements x
}
{
     //Loop if 0
     doSomething...
     break                  //This loop executes once when x reaches 0, then breaks
}
{
     //Loop if -
     doSomethingElse...
     break                 //This loop does something else if x returns FALSE, then breaks
}

If x was a positive number the above code would execute the TRUE loop over and over, decrementing x until it reached 0. Then it would execute the NEUTRAL loop once and break. If x was already 0, it would execute the NEUTRAL loop once and break. If x was negative, it would do some other action and break. Or you could have it do nothing and break as a simple fail-through.

Infinite loops would naturally have to be watched out for just like with any other loop statement but I think debugging such errors would end up being easier. Just put a break point at the beginning of each of the three loops and watch the variable being evaluated.

This control statement could be used to do pretty much anything you would expect from a for loop or a while loop. Combining it with a "do" statement would get a bit complex but could be arranged. It wouldn't replace a switch statement since that can be used to define an arbitrary number of cases.

On the surface the eval statement and choice loop look like elegant, native-ternary flow control statements. At least they look like that to me. Someone who actually has some language design experience would be better suited to judge them or to recommend alternatives.

As for logical operators, the ones in common use are ! (NOT), && (AND) and || (OR). I have already addressed NOT in other posts, so we can focus on the two-input logical operators here.

Here are the equivalent kleene versions of those boolean logical operators:

Boolean              Kleene
&& (AND)            Min
|| (OR)                  Max

By the way, here's a really good explanation of why logical XOR (and by extension XNOR) don't exist in C. http://c-faq.com/misc/xor.dmr.html

I'll skip over the obvious uses of the boolean logical operators. Suffice it to say, they regard each operand as a boolean, so a non-zero value is considered TRUE and a zero value is considered FALSE. The result of the operation is returned as a boolean value.

As for ternary logical operators, it first needs to be pointed out that there are 19,683 of them. Of course the vast majority wouldn't be of much use and it would be a complete joke to expect a language to have vocabulary for all of them. However, I suppose it could be possible for a language to compute the truth table for any logical operator if there were a way to describe it in the source code. Say, with the heptavintimal name for the two-input gate for example:

if (x <A6R> y == NEUT) then...

This way, theoretically any of the possible two-input gates could be used as a logical operator. I don't have a clue how (or why) that would be implemented, but it's an interesting idea.

Putting that aside for the moment, let's address the use of the ternary logical operators that correspond to existing logical operators. They evaluate each operand for its kleene value (FALSE for a negative, NEUT for a zero and TRUE for a positive) and they they return kleene values. Min returns the value of the lesser of the two inputs. Max returns the greater of them. Simple.

The thing to keep in mind is that they can return a NEUT and that this can be used for more expressive control statements. More on that in a later post.

This is just a quick address of an important law in logic. De Morgan's Laws demonstrate the relationship between two basic binary gates, AND and OR. Here they are:

NOT(A AND B) = (NOT A) OR (NOT B)
NOT(A OR B) = (NOT A) AND (NOT B)

These laws have an equivalent function in Kleene's version of ternary logic using the negation gate and the Min and Max two-input gates. This is another reason I liked Kleene's version of ternary logic. Not all of them adhered to De Morgans Laws.

Neg(A Min B) = (Neg A) Max (Neg B)
Neg(A Max B) = (Neg A) Min (Neg B)

There you have it.