-
Zigzag algorithm notes
05/04/2020 at 18:15 • 0 commentsThis log is a bit out of order but I cleaned up my desk last week and want to get these papers off it lest I get back into the same mess I started in.
![]()
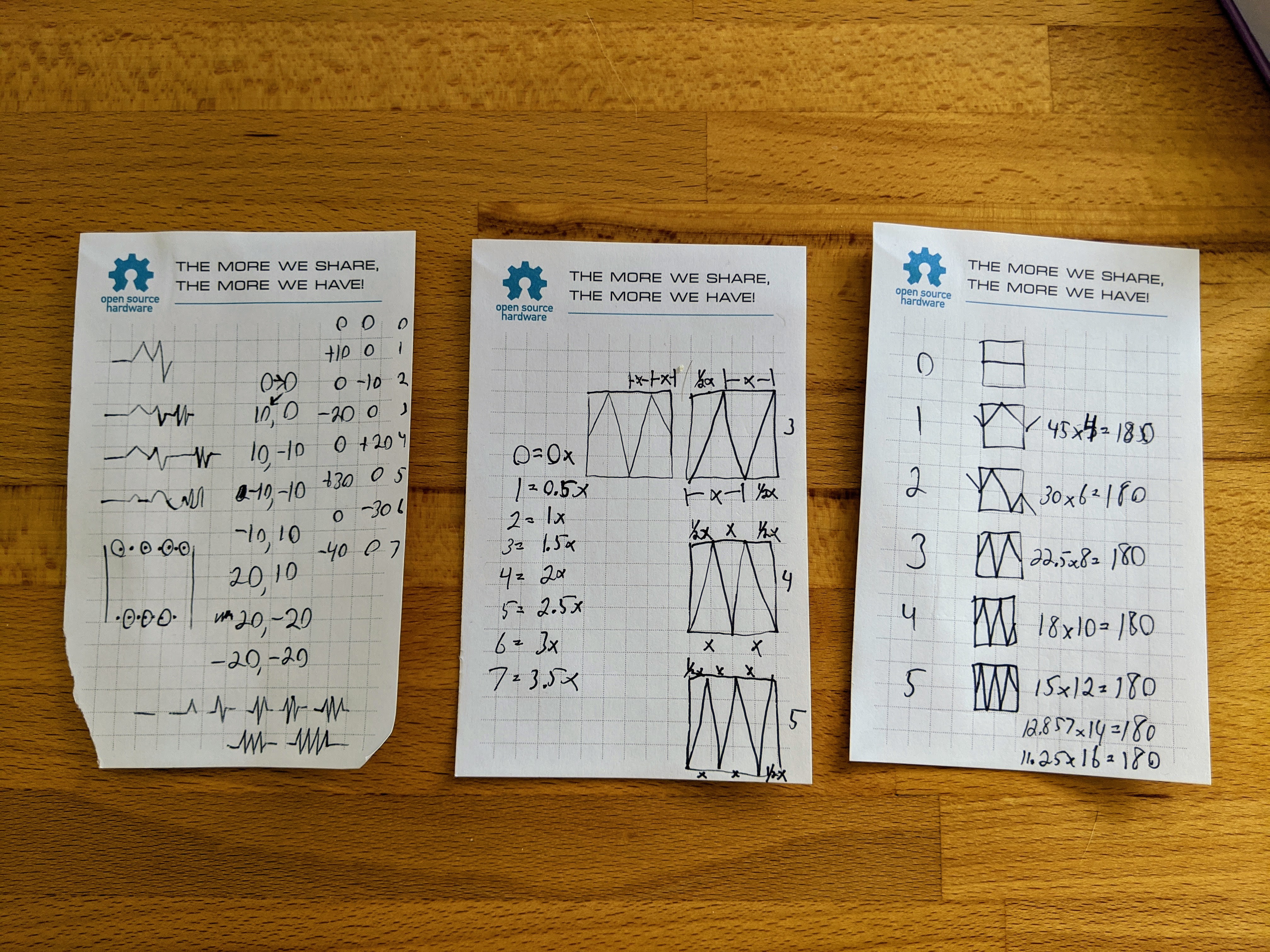
These are my notes on how to write an algorithm for a zigzag within X space given N...N+7 peaks on the zigzags. Issues I encountered on conceptualizing this:
- Tried to use angles at first, that was a complicated mess
- I'm starting on the half-wavelength so tried to shift everything and account later
- Final answer is that it's the number of segments of all combined crest and trough points that is all you need to calculate
Also, the sets of numbers on the right half of the leftmost sheets is the literal points and the delta of those points for the spiral algorithm.
-
Plotting images with zigzag
05/02/2020 at 19:01 • 0 commentsI made two different test images to see how progress is coming along.
Unfortunately these won't actually fit on the bed of the mid-t-bot as a 120mmx120m grid won't leave room for the 8 different levels of zigzag. I'll have to think about how to approach this. Maybe I need to do some zigzag tests on the plotter to find what my max resolution may be.
![]()
![]()
These show promise but bring up a number of things I need to work on:
- Last zigzag direction needs to be tracked. Currently zigzags always start with an upward stroke, but is last zigzag ended with a downward stroke this means an unsightly V shape.
- Need to work on translating this to work on a spiral pattern. This was a quick and easy proof of concept, but the raster approach negates the use of a plotter. I think spiral will look much cooler while being drawn too
- I'm currenlty pre-processing these in Gimp, converting to grayscale indexed images of 120x120 with 8 color palette, and exporting as .h files. It would be cooler if you could supply an image to Python and it would handle all of this
- I'm still not actually generating g-code. I should probably break out all plotting functions to wrapper scripts which could then could turn on or off the g-code generation as well as trigger the turtle commands
-
XOR ZigZag
05/02/2020 at 17:02 • 0 comments![]()
I wanted to try out the zigzag patterns from the last project log. I found a little bug in how a 0 density was treated, but otherwise, drawing this XOR pattern worked out well. Next stop is processing images.
def linesDemo(turtleObj, xlimit, ylimit, steps): for y in range(0, ylimit, steps): turtleObj.penup() turtleObj.setpos(0,y) turtleObj.pendown() for x in range(steps, xlimit, steps): density = (x ^ y) % 8 zigzag(turtleObj, (x,y), steps/2, density)I ran the program which generated the image above with the following settings: linesDemo(stylus, 300, 300, 10)
-
Drawing ZigZags
05/01/2020 at 23:00 • 0 comments![]()
To make my spiral patterns more useful I want to add some contrast element. Seems like drawing a zig-zag pattern is one way to do this as it fills more ink into a given space than merely drawing a straight line.
from turtle import * stylus = Turtle() #stylus.setpos(100,100) def zigzag(turtleObj, endPosition, zigAmplitude, density): if density > 7: print("Warning: Density out of bounds, setting to zero") density = 0 staticAxis = (endPosition[0] - turtleObj.position()[0], endPosition[1] - turtleObj.position()[1]) #Don't zig if somethings wrong with coordiante sets if (staticAxis[0] == 0 and staticAxis[1] == 0) or (staticAxis[0] != 0 and staticAxis[1] != 0): print("Error: can't zig unles one and exactly one X/Y coordinate set is the same") #Just move to the end position and return turtleObj.setpos(endPosition[0],endPosition[1]) return if density == 0: turtleObj.setpos(endPosition[0],endPosition[1]) return if staticAxis[0] == 0: #We should be moving along the Y axis because start and end X coord is the same staticStart = turtleObj.position()[1] peaks = returnZigPoints(staticStart,endPosition[1],density) amplitudeValues = (endPosition[0] + zigAmplitude, endPosition[0] - zigAmplitude) for i in range(len(peaks)): turtleObj.setpos(amplitudeValues[i%2],staticStart+peaks[i]) else: #We're moving along the X axis staticStart = turtleObj.position()[0] peaks = returnZigPoints(staticStart,endPosition[0],density) amplitudeValues = (endPosition[1] + zigAmplitude, endPosition[1] - zigAmplitude) for i in range(len(peaks)): turtleObj.setpos(staticStart+peaks[i],amplitudeValues[i%2]) #Send cursor to the final position turtleObj.setpos(endPosition[0], endPosition[1]) def returnZigPoints(startPoint,endPoint,density): steps = (endPoint-startPoint)/(density+1) #There is 1 more segment between points than there are total points pointset = [steps] for i in range(1,density): pointset.append(pointset[-1]+steps) return pointsetUsing this code:
stylus.setpos(40,0) zigzag(stylus,(80,0),40,7) stylus.setpos(120,0) zigzag(stylus,(160,0),40,3) stylus.setpos(200,0) zigzag(stylus,(240,0),40,1) stylus.setpos(280,0) zigzag(stylus,(320,0),40,5)So if I combine this with a bit of image processing and add it to the spiral patterns I was drawing before, I should be able to make some kind of meaningful abstract representation of 3-bit grayscale. That's next on the challenge list!
-
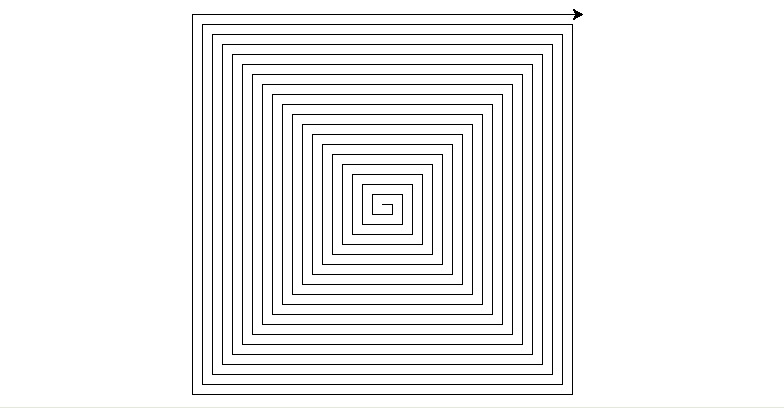
Drawing Spirals
05/01/2020 at 22:52 • 0 commentsI'm working on some code to generate spiral patterns. So far I'm using Turtle in Python to simulate the pen plotter (you may remember this from the Apple ][)
from turtle import * stylus = Turtle() #stylus.setpos(100,100) def drawSpiral(turtleObj,limit, steps): #0=right, 1=down, 2=left, 3=up increment = 0 counter = 1 while turtleObj.position()[0] < limit and turtleObj.position()[1] < limit: #if odd if counter%2 != 0: #increase by 10 if increment < 0: increment -= steps else: increment += steps #change X turtleObj.setpos(turtleObj.position()[0]+increment,turtleObj.position()[1]) #if even else: #flip polarity increment = increment * -1 #change Y turtleObj.setpos(turtleObj.position()[0],turtleObj.position()[1]+increment) counter += 1Which when run using drawSpiral(stylus,191,10) gives us the nice demo below. This isn't spitting out g-code, but it shouldn't be hard to add that in when ready.
![]()
-
Hilbert Curves
12/20/2019 at 07:25 • 1 commentI grabbed some simple Hilbert Curve code from this thread:
https://stackoverflow.com/questions/7218269/hilbert-curve-analysis
And added the ability to export gcode instructions as the recursive function played out. The result is very satisfying as the pen is never picked up.
![]()
Code for this is available in the files section.
 Mike Szczys
Mike Szczys