-
Stutter
02/11/2025 at 11:38 • 0 commentsPlaying a bit with PEAC w4 :
#include <stdint.h> uint8_t PEAC_XC=1, // the 5-bit part PEAC_Y=0; // 4-bit #include <stdio.h> int main() { int i=0; do { printf("% 3d: % 3d % 3d \n", i, PEAC_XC, PEAC_Y); // split uint8_t PEAC_X = PEAC_XC & 15; PEAC_XC >>= 4; // PEAC scrambler PEAC_XC += PEAC_X + PEAC_Y; PEAC_Y = ( PEAC_X + 0 ) & 15; i++; } while (i <= 136); return 0; }W4 is a maximal, not perfect, orbit so there are "only" 135 iterations. But the output sequence, either PEAC_Y or PEAC_XC, shows that some numbers repeat but only in consecutive pairs
XC Y 0: 1 0 1: 1 1 2: 2 1 3: 3 2 4: 5 3 5: 8 5 6: 13 8 7: 21 13 8: 19 5 9: 9 3 10: 12 9 11: 21 12 12: 18 5 13: 8 2 14: 10 8 15: 18 10 16: 13 2 17: 15 13 18: 28 15 19: 28 12 20: 25 12 21: 22 9 22: 16 6 23: 7 0 24: 7 7 25: 14 7 26: 21 14 27: 20 5 28: 10 4 29: 14 10 30: 24 14 31: 23 8 32: 16 7 33: 8 0 34: 8 8 35: 16 8 36: 9 0 37: 9 9 38: 18 9 39: 12 2 40: 14 12This "stutter" might be a sort of "signature" of a PEAC PRNG, which is why PEAC is better used as a scrambler IMHO.
Now, is this "stutter" a defect ? Not really. On the primary orbit of w4 above,
- the number 2 appears 11 times and "stutters" 2 times.
- 3 appears 9 times and stutters 1×.
- 4 appears 12 times and stutters 1×
So in a maximal (and not perfect) orbit, there are some imbalances.
.
-
Init vectors
02/08/2025 at 14:34 • 0 commentsUntil now I use 0xABCD and 0x4567 to initialise the PEAC16x2 algorithms, but they don't propagate the carries enough. This comes from the fact that even and odd hex digits are "aligned" so there are at least 4 bits that are identical at each position. Ideally : X|Y=1 for each bit position.
One way to solve this is to offset the digits by one position : X=0xBCDE and Y=0x4567
This is slightly better:
>>> hex( 0xABCD | 0x4567 ) '0xefef' >>> hex( 0xBCDE | 0x4567 ) '0xfdff'Time to update all the other references...
-
a POSIXy rand()
02/07/2025 at 18:09 • 0 commentsAfter the last log, here's a first draft of a POSIX-compliant PRNG to replace the dumb congruential generator. The combined period should exceed 2^64 yet no heavy operation (like multiplies or moduli) are used. Of course I should test the quality of the output...
#include <stdint.h> #define RAND_MAX 32767 /* From the spec: If rand() is called before any calls to srand() are made, the same sequence shall be generated as when srand() is first called with a seed value of 1. */ uint32_t rand_LFSR = 1, rand_PEAC_XC = 1; uint16_t rand_PEAC_Y = 0; void srand(unsigned seed) { if (seed) rand_LFSR = seed; else rand_LFSR = 0x89ABCDEFUL; rand_PEAC_XC = seed; rand_PEAC_Y = ~seed & 1; } int rand(void) { // LFSR PRNG : uint32_t t = rand_LFSR & 1; rand_LFSR >>= 1; if (t) rand_LFSR ^= 0x82608EDB; // CRC32 poly // PEAC scrambler : uint16_t rand_X = rand_PEAC_XC; // 16 LSB rand_PEAC_XC = (rand_PEAC_XC >> 16) + rand_X + rand_PEAC_Y; rand_PEAC_Y = rand_X + rand_LFSR; // 16 LSB return rand_PEAC_XC & RAND_MAX; }Let's see how far this one flies.
The first compile and run go smoothly:
[yg@ygrand]$ gcc -Wall -Os -o test_ygrand test_ygrand.c && ./test_ygrand 0000000000000001 0000111011011101 0101100010010100 0100110001001101 0110000110011000 0000110001000000 0000111111001111 0110110100001010 0110001101111111 0100001111011101 0001111011001111 0001111001100110 0101000000111101 0011010111111011 0010100111100101 0111000110110111 0110010010000111 0000000011101101 0011101011001100 0010000000101001 0100110100101110 0110011001110011 ...The PRNG is not even initialised, only using the default value of 1, and it immediately reached a high scrambling state. Calling srand() is a must though, and should call rand() a few times itself for "better results".
Initialising with srand(0) also gives a good-looking sequence with the help of some extra calls to rand().
The Hamming distance between consecutive numbers looks good after 10000000000 iterations. Note that slot 16 is cleared because only 15 bits are provided at each step.
0 : 305938 1 : 4575646 2 : 32047057 3 : 138854426 4 : 416575520 5 : 916453074 6 : 1527396508 7 : 1963876973 8 : 1963793753 9 : 1527393214 10 : 916423856 11 : 416545995 12 : 138835287 13 : 32036947 14 : 4580472 15 : 305334 16 : 0
The peak is well centered around slots 7 and 8, the histogram is nicely symmetrical.
For comparison, I made a "fake PRNG" that pulls data out of /dev/random and here is the histogram:
0 : 305586d 1 : 4579839d 2 : 32047565d 3 : 138857968d 4 : 416545970d 5 : 916470025d 6 : 1527349897d 7 : 1963799989d 8 : 1963842436d 9 : 1527391622d 10 : 916495473d 11 : 416539621d 12 : 138850583d 13 : 32042754d 14 : 4575830d 15 : 304842d 16 : 0d
It's pretty spot on but that's only one of many aspects to check.
___________________________________________________
Update : I fixed the init values so it matches srand(1) after 3 calls to rand().
uint32_t rand_LFSR = 0x61A864DB, rand_PEAC_XC = 0x00015894; uint16_t rand_PEAC_Y = 0xF3B8;I've put the files there ygrand.tgz
-
a rand()... or so.
02/03/2025 at 15:11 • 0 commentsI have recently received inquiries from two projects :
Both are interested by a new/better implementation of the rand() function and it would be beneficial to merge these two requests.
First, I need a good definition of the requirements : size of the state, width of the registers... I'll first try a typical version with two variables, not much larger than the historic implementation (congruential generators have only one register). I suppose that the variable seed must be adapted...
Already, a limitation : POSIX defines rand() as returning an int limited by RAND_MAX>=32767
The <stdlib.h> header shall define the following macros which shall expand to integer constant expressions: {RAND_MAX} Maximum value returned by rand(); at least 32767.On my local installation, /usr/include/stdlib.h says
/* The largest number rand will return (same as INT_MAX). */ #define RAND_MAX 2147483647(Note: yet another reason that POSIX IS DEAD ! You CAN'T know your local size until you test the system, instead of being sure to have a certain width that lets you program comfortably everywhere).
.
Now, the recent libc has more than one function :void srand(unsigned); void srand48(long); void srandom(unsigned); .... int rand(void); int rand_r(unsigned *); long jrand48(unsigned short [3]); long lrand48(void); long mrand48(void); long nrand48(unsigned short [3]); long random(void); double drand48(void); double erand48(unsigned short [3]);So it's a whole crazy mess... and https://pubs.opengroup.org/onlinepubs/9699919799/functions/srand.html adds more mess. But who uses it anyway ?
For TrapC,
We need
- a crypto random for crypto stuff,
- a streaming random for telecom stuff,
- a repeatable random for scientific stuff,
- and a good checksum hash that isn't random for hash tables...
crypto_random_t cr;// for casino real-money gaming packet_random_t sr;// for encrypted streaming transmission pseudo_random_t rr("test 1");// for repeatable A/B testing hash32_t h32("hello world"); hash64_t h64("hello world");And constructors to automatically do the right thing to seed generators. An application programmer doesn't need to know how they work to use them.
.
Let's go back to POSIX.
-
Checksum w16 on 6309
02/02/2025 at 01:02 • 0 commentsMy friend François designed a SBC sporting a Hitachi 6309E, a faster and extended version of the venerable Motorola 6809. Looking at its instruction set table, I find that it has instructions that handle 16 bits at once on the D register (made of the A and B byte accumulators). This is actually pretty suitable for a PEAC16×2 algorithm, which is way better than the xorsum currently used...
But François said :
- the program must use the LEAST number of bytes
- the checksum is reduced down to one byte
- the scanning range can be from one to 2^16 bytes.
PEAC16×2 works with pairs of bytes so the eventual extra odd byte must be handled separately at the end. And there is no notion of alignment, but the 6809 is a Big Endian machine. Since the constraint is placed on the code size and not the speed, the algorithm loop would work on individual bytes, not 16-bit words.
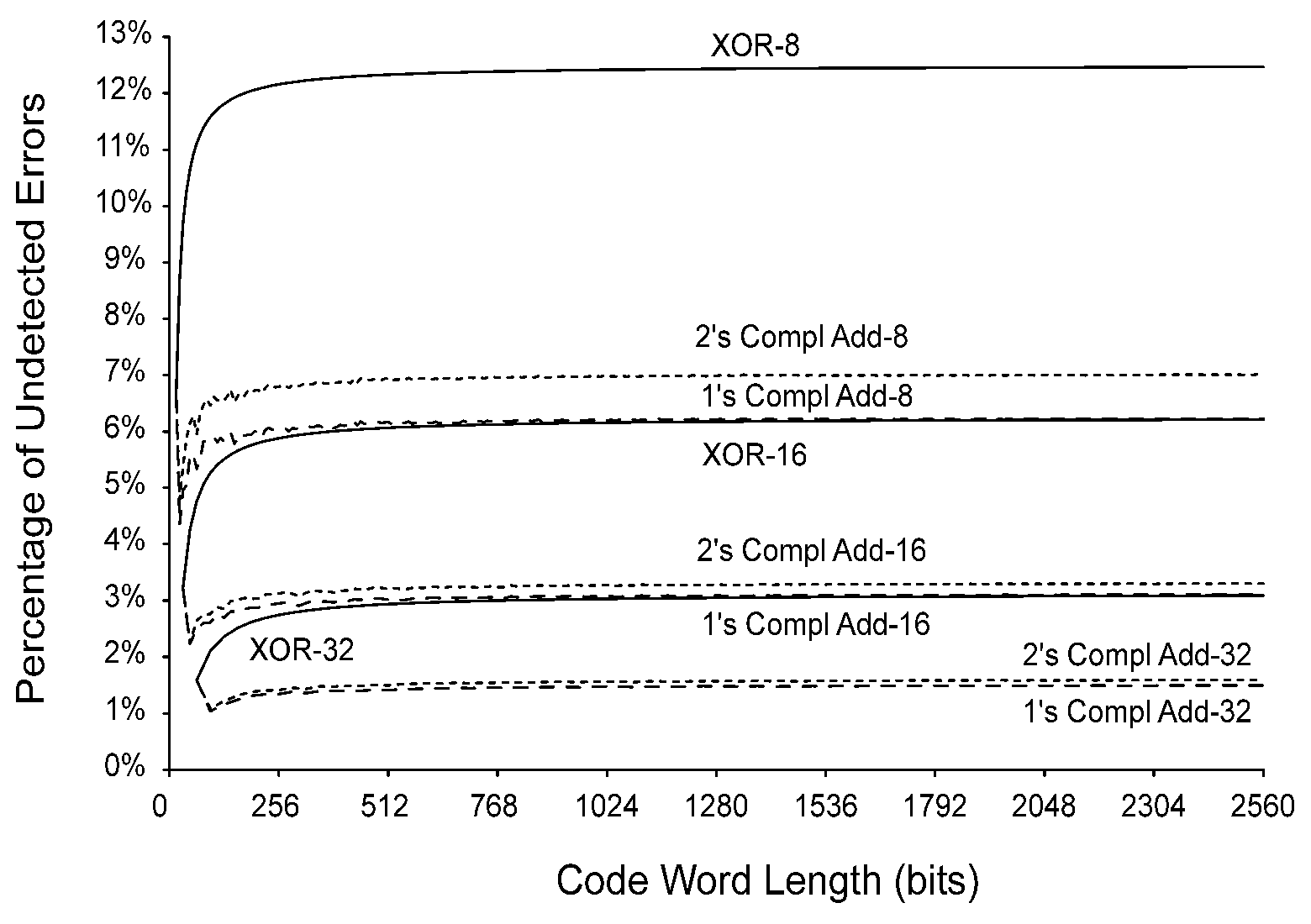
At first look, the algorithm is more complex and larger than xorsum but a first enhancement would replace the xor with add, and reuse the carry: this is not foolproof but requires very little effort to implement.
Replacing xor8 with adc8 divides the error rate by two :
![]()
.
-
PEAC modulo
11/05/2024 at 13:43 • 0 commentsThe log 122. Funky modulo has some funny/funky/hackmemesque observations for lower-level implementations, but what about the higher level ?
It only occured to me today, thinking about gPEAC, that the wraparound of the sum S goes like
S' = (S / m) + (S % m) Not sure how it's going to help with analysing the large-scale behaviour though, it's above my pay grade.
-
Hashing with PEAC39/2
11/04/2024 at 06:02 • 0 commentsLook at the logs
155. More candidates and 741454
156. The good numbers
163. Hash enhancementsThe scan has harvested a very interesting number:
- m= 2^(39/2)-1 = 741454 = 2×7×211×251 = 10110101000001001110b is known perfect, using 20-bit registers.
- orbit = 549.754.775.568 = 111111111111111111100000010100000010000 in binary, takes about 8 minutes to scan.
- offset: o = 0111.11010101.11010101 = 7D5D5h = 513493 = 107×4799
With these parameters, we get a very effective hash algorithm for text strings, 2 bytes at a time (among others). Aside from the PEAC structure itself and its Fibonacci/Pisano scrambling with the addition,
- The modulus is conditional and increases the scrambling by seeding avalanche with 8 more bits,
- The offset is unconditional and increases the avalanche in normal ASCII characters, while also triggering "End Around Carry" much more often than normally with empty input.
TODO
- Check common divisors of 741454 | 513493 : none !
- Check the orbit length of PRNG with offset 513493
For this, the "scanner" must be modified to add the offset, which creates all kinds of ... hmmm algorithmic questions. Fortunately there are two ways to design a checksum with PEAC : single-carry or dual-carry. Single-carry is less parallel but uses a bit fewer operations. It's easy to adapt with the binary PEAC but I realise it's the first time I do this operation on a gPEAC: it's my first gPEAC checksum.
.
.
-
PEAC w64 checksum : x86-64 edition
10/18/2024 at 01:25 • 2 commentsI did it !
The fastest checksum (128 bits per loop) that is also solid (unlike Fletcher/Adler etc.)
Here is the C source code:
#include <stdint.h> #define PEAC64_INIT1 (0x7777777777777777ULL) #define PEAC64_INIT2 (0xDDDDDDDDDDDDDDDDULL) void w64_checksum_asm( uint64_t *buffer, uint64_t *r, uint64_t *s, uint64_t WordPairs) { uint64_t X=WordPairs, Y=PEAC64_INIT2, I=PEAC64_INIT1; asm volatile("\n\t" " addq %[I], %[X] \n\t" // X += I; " clc \n\t" // C = 0; " \n\t" " test %[WordPairs],%[WordPairs] \n\t" // WordPairs=0? " jz empty_buffer \n\t" " \n\t" " .p2align 4 \n\t" "innerloop: \n\t" " adcq %[X] , %[Y] \n\t" // Y += X " adcq (%[buffer]), %[X] \n\t" // X += *buffer " \n\t" " adcq %[Y], %[X] \n\t" // X += Y " adcq 8(%[buffer]), %[Y] \n\t" // Y += buffer[1] " \n\t" " lea 16(%[buffer]), %[buffer] \n\t" // buffer+=2 " decq %[WordPairs] \n\t" // WordPairs-- " jnz innerloop \n\t" // while (WordPairs); " \n\t" "empty_buffer: \n\t" " adcq %[X], %[Y] \n\t" // Y += X " adcq %[I], %[X] \n\t" // X += PEAC64_INIT1 : // outputs [X] "+r" (X), [Y] "+r" (Y), [WordPairs] "+r" (WordPairs), [buffer] "+r" (buffer) : // inputs [I] "r" (I) : // clobber "cc" ); *s = X; *r = Y; }And gcc -O3 -S compiles it down to:
w64_checksum_asm: movabsq $-2459565876494606883, %rax movq %rcx, %r9 movabsq $8608480567731124087, %r8 addq %r8, %rcx clc test %r9,%r9 jz empty_buffer .p2align 4 innerloop: adcq %rcx , %rax adcq (%rdi), %rcx adcq %rax, %rcx adcq 8(%rdi), %rax lea 16(%rdi), %rdi decq %r9 jnz innerloop empty_buffer: adcq %rcx, %rax adcq %r8, %rcx movq %rcx, (%rdx) movq %rax, (%rsi) retThat's it !
With this, you get a 128-bit signature of a memory block, which can be filled with read(2) for example. It is hard to do significantly better now, because the memory becomes the bottleneck.
One last trick is the use of ADCX and ADOX opcodes, to implement a separate carry structure and break the 4-instruction carry chain into two halves. But it won't work because decq affects the overflow flag.
Now I have to check the primary orbit of w64...
-
TODO: scans
10/17/2024 at 16:48 • 0 commentsThings have progressed again and a new branch of the PEAC family has appeared, tuned for SW implementations where the masking operation is simply skipped. This completely changes the mathematics of the system.
Below are 2 examples with w26 and w31 which are "extended" (hence the "+") by not masking the sum after the addition.
![]()
w26 is known to be "perfect" but w31 does not pass the sieve.
However messing with the MSB(s) changes the rules and everything has to be reconsidered now. The difficulty is that the 32-bit words require immense amounts of computations and the others (based on 64-bit registers) are even worse.
So a thorough computation exploration is required for
- w26+
- w31 (not holding my breath)
- w31+
- w63 (passes sieve)
- w63+
- w64
At least a first estimate of computability of the primary orbit.
Furthermore, another class of gPEAC needs to be evaluated: the 1.5× types, called "pseudo-binary", for use in Line Scramblers (see the previous logs such as 167. Line encoding with PEAC: it's alive) : the 2 MSB of the modulo are 1 and the rest is 0. These are powers of 2 multiplied by 3, so the subtraction only requires processing a few MSB and not the whole word. At least a few of these numbers should be in the list of the moduli I had scanned last year. I have found 3 only...
a=3 ; for i in $(seq 40); do a=$(($a*2)); echo $a; done 6 : perfect 12 : 10P 24 : maximal 48 : maximal 96 : maximal 192 : 191M 186P 384 : 380M, 378P, 374P 768 : 763M, 761M, 754P, 750P, 746P (w8) 1536 : 1528M, 1526P, 1516M, 1511M, 1504M, 1501M, 1498P 3072 : 3060M, 3038P, 3036M, 3018P 6144 : 6128M, 6118P, 6106P 12288 : 12280M, 12254P 24576 : 24563M, 24551M, 24549M, 24546P 49152 : 49050, 49084, 49094, 49128 98304 : 98300, 98298, 98285 98264 98254 196608 : 196605M 196598P 196594P (w16) 393216 : 393208M 393195M 393186P 786432 : 786418P 786403M 786388M 786390P 786391M 1572864 3145728 6291456 12582912 25165824 50331648 100663296 201326592 402653184 805306368 1610612736 3221225472 6442450944 12884901888 25769803776 51539607552 103079215104 206158430208 412316860416 824633720832 1649267441664 3298534883328 ......
Stay tuned.
-
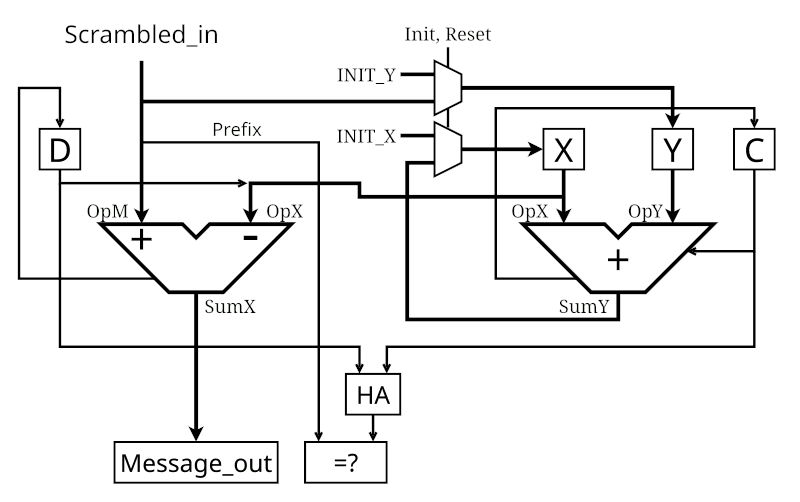
PEACLS error detection (and correction?)
10/13/2024 at 17:49 • 4 commentsI added error detection, it was in fact very simple and it seems to work very well.
![]()
I started playing with it, for example adding one bit of noise on the channel (in bold, scroll the listing).
Init=1 In=0000000000000000 Scr:10-0000000000000000 Sc2:10-0000000000000000 Out=0000000000000000 OK=U Init=0 In=0000000000000000 Scr:00-0000000000000001 Sc2:00-0000001000000001 Out=0000001000000000 OK=1 Init=0 In=0000000000000000 Scr:00-0000000000000001 Sc2:00-0000000000000001 Out=0000000000000000 OK=1 Init=0 In=0000000000000000 Scr:00-0000000000000010 Sc2:00-0000000000000010 Out=1111111000000000 OK=0 Init=0 In=0000000000000000 Scr:00-0000000000000011 Sc2:00-0000000000000011 Out=1111110111111111 OK=0 Init=0 In=0000000000000000 Scr:00-0000000000000101 Sc2:00-0000000000000101 Out=1111110111111111 OK=0 Init=0 In=0000000000000000 Scr:00-0000000000001000 Sc2:00-0000000000001000 Out=1111110111111111 OK=0 Init=0 In=0000000000000000 Scr:00-0000000000001101 Sc2:00-0000000000001101 Out=1111110111111111 OK=0 Init=0 In=0000000000000000 Scr:00-0000000000010101 Sc2:00-0000000000010101 Out=1111110111111111 OK=0 Init=0 In=0000000000000000 Scr:00-0000000000100010 Sc2:00-0000000000100010 Out=1111110111111111 OK=0
The error is not detected immediately but the OK flag is consistently stuck to 0 afterwards.
What this means is : the epilogue of a packet should have 2 padding words to ensure the last data word has been correctly transmitted.
Another interesting aspect is the efficiency of the 2 prefix bits : even though they are not flipped during transmission, the reconstructed bits mismatch anyway ! So it does not matter so much that the prefix does not use the whole coding range, error detection occurs anyway and the carries help prevent all-0 words.
Even more interesting is the bit pattern of the altered reconstructed word: after 3 words, the output contains the inverse of the alteration ! Is this an opportunity for error correction ?
Further wiggling shows that it's a corner case, but finishing the packet with 2 blank words certainly detects multiple errors. Get the source code here.
PEAC Pisano with End-Around Carry algorithm
Add X to Y and Y to X, says the song. And carry on.
 Yann Guidon / YGDES
Yann Guidon / YGDES