Fitting a Quadratic Bezier Curve to Point Data

Cubic Code Results

 While the results are good it is not exact like the piece-wise quadratic bezier code.

I quess a fourth order bezier would bit better.

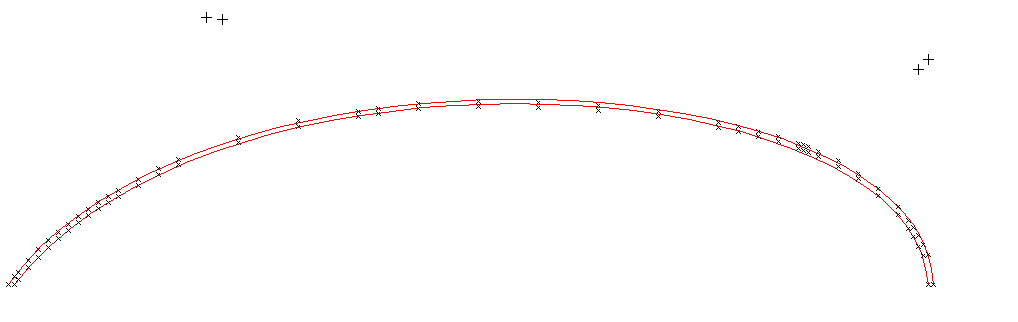
Hers is the cubic match:

Note the bezier cuves are too wide just aft of the maxium beam and too narrow near the stern.

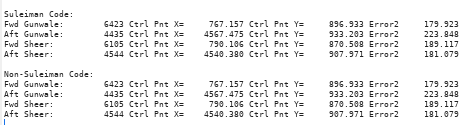
Here are the control points:

Here is the full code:

// Include libraries
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>
#include <math.h>

// Include in local directory:
#include "ezxdisp.h"
// Library: libezx.a 
// Linker: -L. -lezx -lX11 -lm

// EZX window size
static int width=1200;
static int height=700;
static double scale=0.2;
// EZX display
static ezx_t *disp;

void PlotBezier(double Xi[],double Yi[],double Ti[],int Ni,double *Bx1,double *By1,double *Bx2,double *By2)
{
  // Plot Fitted Bezier Curve  
  double X0,Y0,X1,Y1;
  X1=Xi[0];
  Y1=Yi[0];
  for (int i=1;i<Ni;i++) {
	double t=1.0*i/(Ni-1);
  	double s=(1.0-t);
	X0=X1;
	Y0=Y1;
    X1=s*s*s*Xi[0]+3*s*s*t**Bx1+3*s*t*t**Bx2+t*t*t*Xi[Ni-1];
    Y1=s*s*s*Yi[0]+3*s*s*t**By1+3*s*t*t**By2+t*t*t*Yi[Ni-1];
    ezx_line_2d(disp,scale*X0,height/2-scale*Y0,scale*X1,height/2-scale*Y1,&ezx_red,1);
  }
  
  // Plot Fitted Control Point (B1)
  ezx_line_2d(disp,scale**Bx1-5,height/2-scale**By1,scale**Bx1+5,height/2-scale**By1,&ezx_black,1);
  ezx_line_2d(disp,scale**Bx1,height/2-scale**By1-5,scale**Bx1,height/2-scale**By1+5,&ezx_black,1);

  // Plot Fitted Control Point (B2)
  ezx_line_2d(disp,scale**Bx2-5,height/2-scale**By2,scale**Bx2+5,height/2-scale**By2,&ezx_black,1);
  ezx_line_2d(disp,scale**Bx2,height/2-scale**By2-5,scale**Bx2,height/2-scale**By2+5,&ezx_black,1);
  
  // Plot Input points     
  for (int i=0;i<Ni;i++) {
    ezx_line_2d(disp,scale*Xi[i]-2,height/2-scale*Yi[i]-2,scale*Xi[i]+2,height/2-scale*Yi[i]+2,&ezx_black,1);
    ezx_line_2d(disp,scale*Xi[i]+2,height/2-scale*Yi[i]-2,scale*Xi[i]-2,height/2-scale*Yi[i]+2,&ezx_black,1);
  }
  
  return;
}


void FitBezier(double Xi[],double Yi[],double Ti[],int Ni,double *x1,double *y1,double *x2,double *y2)
{
  double Bx0=Xi[0];
  double By0=Yi[0];
  double Bx1=*x1;
  double By1=*y1;
  double Bx2=*x2;
  double By2=*y2;
  double Bx3=Xi[Ni-1];
  double By3=Yi[Ni-1];
  double Ex1,E1x1,E2x1;
  double Ey1,E1y1,E2y1;
  double Ex2,E1x2,E2x2;
  double Ey2,E1y2,E2y2;
  double t,e2=0.0;
  do {
    E1x1=0.0;
    E2x1=0.0;
    E1y1=0.0;
    E2y1=0.0;
    E1x2=0.0;
    E2x2=0.0;
    E1y2=0.0;
    E2y2=0.0;
    e2=0.0;
    // Solve all t
    for (int i=1;i<Ni-1;i++) {

      double Et=0.0;
      t=Ti[i]; // Initial t
      // printf("i=%3d t=%12.6lf",i,t);
      do {
        double f1=(t*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+t*t*(3*Bx0-6*Bx1+3*Bx2)+t*(-3*Bx0+3*Bx1)+(Bx0-Xi[i]))*(6*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+4*t*(3*Bx0-6*Bx1+3*Bx2)+2*(-3*Bx0+3*Bx1))
                 +(t*t*t*(-By0+3*By1-3*By2+By3)+t*t*(3*By0-6*By1+3*By2)+t*(-3*By0+3*By1)+(By0-Yi[i]))*(6*t*t*(-By0+3*By1-3*By2+By3)+4*t*(3*By0-6*By1+3*By2)+2*(-3*By0+3*By1));
        double f2=(3*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+2*t*(3*Bx0-6*Bx1+3*Bx2)+(-3*Bx0+3*Bx1))*(6*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+4*t*(3*Bx0-6*Bx1+3*Bx2)+2*(-3*Bx0+3*Bx1))
                 +(t*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+t*t*(3*Bx0-6*Bx1+3*Bx2)+t*(-3*Bx0+3*Bx1)+(Bx0-Xi[i]))*(12*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+4*(3*Bx0-6*Bx1+3*Bx2))
                 +(3*t*t*(-By0+3*By1-3*By2+By3)+2*t*(3*By0-6*By1+3*By2)+(-3*By0+3*By1))*(6*t*t*(-By0+3*By1-3*By2+By3)+4*t*(3*By0-6*By1+3*By2)+2*(-3*By0+3*By1))
                 +(t*t*t*(-By0+3*By1-3*By2+By3)+t*t*(3*By0-6*By1+3*By2)+t*(-3*By0+3*By1)+(By0-Yi[i]))*(12*t*(-By0+3*By1-3*By2+By3)+4*(3*By0-6*By1+3*By2));
        Et=f1/f2;
        t=t-Et;
      } while (Et*Et>1e-8); // Error ~0.001      
      Ti[i]=t;
      e2=e2+(Bx0*(1-t)*(1-t)*(1-t)+3*Bx1*(1-t)*(1-t)*t+3*Bx2*(1-t)*t*t+Bx3*t*t*t-Xi[i])*(Bx0*(1-t)*(1-t)*(1-t)+3*Bx1*(1-t)*(1-t)*t+3*Bx2*(1-t)*t*t+Bx3*t*t*t-Xi[i])
           +(By0*(1-t)*(1-t)*(1-t)+3*By1*(1-t)*(1-t)*t+3*By2*(1-t)*t*t+By3*t*t*t-Yi[i])*(By0*(1-t)*(1-t)*(1-t)+3*By1*(1-t)*(1-t)*t+3*By2*(1-t)*t*t+By3*t*t*t-Yi[i]);
      // printf(" -> t=%12.6lf Et*Et=%12.6lf",t,Et*Et);getchar();

      // WRT: Bx1
      E1x1=E1x1+6*t*(t*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+t*t*(3*Bx0-6*Bx1+3*Bx2)+t*(-3*Bx0+3*Bx1)+(Bx0-Xi[i]))*(t*t-2*t+1);
      E2x1=E2x1+18*t*t*(t*t-2*t+1)*(t*t-2*t+1);
      E1y1=E1y1+6*t*(t*t*t*(-By0+3*By1-3*By2+By3)+t*t*(3*By0-6*By1+3*By2)+t*(-3*By0+3*By1)+(By0-Yi[i]))*(t*t-2*t+1);
      E2y1=E2y1+18*t*t*(t*t-2*t+1)*(t*t-2*t+1);

      // WRT: Bx2
      E1x2=E1x2+6*t*t*(t*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+t*t*(3*Bx0-6*Bx1+3*Bx2)+t*(-3*Bx0+3*Bx1)+(Bx0-Xi[i]))*(1-t);
      E2x2=E2x2+18*t*t*(1-t)*(1-t);
      E1y2=E1y2+6*t*t*(t*t*t*(-By0+3*By1-3*By2+By3)+t*t*(3*By0-6*By1+3*By2)+t*(-3*By0+3*By1)+(By0-Yi[i]))*(1-t);
      E2y2=E2y2+18*t*t*(1-t)*(1-t);

    }
    
    Ex1=E1x1/E2x1;
    Ey1=E1y1/E2y1;   
    Bx1=Bx1-Ex1;
    By1=By1-Ey1;
    Ex2=E1x2/E2x2;
    Ey2=E1y2/E2y2;   
    Bx2=Bx2-Ex2;
    By2=By2-Ey2;       

  } while (Ex1*Ex1+Ey1*Ey1+Ex2*Ex2+Ey2*Ey2>1e-8); // Error ~0.001
  *x1=Bx1;
  *y1=By1;
  *x2=Bx2;
  *y2=By2;
  // printf("e2= %15.6lf  ",e2);  
  return;
}

int main(int argc,char **argv) {
  // Unused parameters
  (void)argc;
  (void)argv;

  // Beam (including gunwale)
  const int N1=43;
  double X1[]={50,83,100,150,200,250,300,350,400,450,500,550,600,700,
	800,900,1200,1500,1800,1900,2100,2400,2700,3000,3300,3600,3700,
	3800,3900,4000,4025,4050,4100,4200,4300,4400,4500,4550,4575,4600,
	4625,4650,4675};
  double Y1[]={25,64,84,144,196,241,284,325,363,397,431,463,492,547,
	602,650,760,841,890,905,929,938,934,918,886,835,811,787,763,730,
	721,713,690,644,580,504,413,344,310,270,223,175,25};
  double* T1=(double*)calloc(N1,sizeof(double));
  for (int i=0;i<N1;i++) T1[i]=1.0*i/(N1-1);
  
  // Beam (excluding gunwale)
  const int N2=41;
  double X2[]={
	83,100,150,200,250,300,350,400,450,500,550,600,700,800,900,1200,
	1500,1800,1900,2100,2400,2700,3000,3300,3600,3700,3800,3900,4000,
	4025,4050,4100,4200,4300,4400,4500,4550,4575,4600,4625,4650
  };
  double Y2[]={25,46,109,160,207,251,294,331,367,401,433,463,519,574,
	623,733,815,864,879,904,913,909,893,861,810,786,762,737,703,695,
	685,662,615,551,470,371,302,263,215,169,25};
  double* T2=(double*)calloc(N2,sizeof(double));
  for (int i=0;i<N2;i++) T2[i]=1.0*i/(N2-1);
  

  disp=ezx_init(width,height,"CubicBezier Curve Fit");
  ezx_set_background(disp,&ezx_white);

    printf("%s\n","Gunwale:");
    double Bx1=1023.147;
    double By1=1349.780;
    double Bx2=4651.200;
    double By2=1157.687;
    Bx1=(2*X1[0]+X1[N1-1])/3;
    By1=(2*Y1[0]+Y1[N1-1])/3;
    Bx2=(X1[0]+2*X1[N1-1])/3;
    By2=(Y1[0]+2*Y1[N1-1])/3;
    FitBezier(X1,Y1,T1,N1,&Bx1,&By1,&Bx2,&By2);
    PlotBezier(X1,Y1,T1,N1,&Bx1,&By1,&Bx2,&By2);
    printf("  X1=%12.4lf  Y1=%12.4lf  X2=%12.4lf  Y2=%12.4lf\n",Bx1,By1,Bx2,By2);

    printf("%s\n","Beam:");
    Bx1=1048.996;
    By1=1314.140;
    Bx2=4623.123;
    By2=1124.916;
    Bx1=(2*X2[0]+X2[N2-1])/3;
    By1=(2*Y2[0]+Y2[N2-1])/3;
    Bx2=(X2[0]+2*X2[N2-1])/3;
    By2=(Y2[0]+2*Y2[N2-1])/3;
    FitBezier(X2,Y2,T2,N2,&Bx1,&By1,&Bx2,&By2);
    PlotBezier(X2,Y2,T2,N2,&Bx1,&By1,&Bx2,&By2);
    printf("  X1=%12.4lf  Y1=%12.4lf  X2=%12.4lf  Y2=%12.4lf\n",Bx1,By1,Bx2,By2);
     
  ezx_redraw(disp);
  while (!ezx_isclosed(disp));
  ezx_quit(disp);
      
  return 0;
}

I think it is time to get back to the Lynaes 14 design.

AlanX

Code Rebuild

I rebuilt the code for a different staing point. Instead of:

  B(t)=(1-t)^2*B0+2*t*(1-t)*B1+t^2*B2

I refacted the equation to:
    B(t)=(B0-2*B1+B2)*t^2+2*(B1-B0)*t+B0

The error squared for each "t" is:

  e^2=((Bx0-2*Bx1+Bx2)*t^2+2*(Bx1-Bx0)*t+Bx0-Xi)^2

        +((By0-2*By1+By2)*t^2+2*(By1-By0)*t+By0-Yi)^2

This equation (e2) calculates the square of distance between the interpolated point (Xi,Yi) from the closest point on the "trial" Bezier curve.

The updated procedure is:

void FitBezier(double Xi[],double Yi[],double Ti[],int Ni,double *x1,double *y1)
{
  double Bx0=Xi[0];
  double By0=Yi[0];
  double Bx1=*x1;
  double By1=*y1;
  double Bx2=Xi[Ni-1];
  double By2=Yi[Ni-1];
  double Ex,E1x1,E2x1;
  double Ey,E1y1,E2y1;
  double t;
  do {
    E1x1=0.0;
    E2x1=0.0;
    E1y1=0.0;
    E2y1=0.0;
    // Solve all t
    for (int i=1;i<Ni-1;i++) {
      // Solve t
      double b4=(Bx0-2*Bx1+Bx2)*(Bx0-2*Bx1+Bx2)+(By0-2*By1+By2)*(By0-2*By1+By2);
      double b3=(Bx0-2*Bx1+Bx2)*(Bx1-Bx0)+(By0-2*By1+By2)*(By1-By0);
      double b2=2*(Bx1-Bx0)*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)*(Bx0-Xi[i])+2*(By1-By0)*(By1-By0)+(By0-2*By1+By2)*(By0-Yi[i]);
      double b1=(Bx1-Bx0)*(Bx0-Xi[i])+(By1-By0)*(By0-Yi[i]);
      // double b0=(Bx0-Xi[i])*(Bx0-Xi[i])+(By0-Yi[i])*(By0-Yi[i]);
      double Et=0.0;
      t=Ti[i]; // Initial t
      do {
        double Et1=4*t*t*t*b4+12*t*t*b3+4*t*b2+4*b1;
        double Et2=12*t*t*b4+24*t*b3+4*b2;
        Et=Et1/Et2;
        t=t-Et;
      } while (Et*Et>1e-6); // Error ~0.001      
      Ti[i]=t;
      E1x1=E1x1+(-4*(Bx0-2*Bx1+Bx2))*t*t*t*t+4*(-2*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2))*t*t*t+4*(2*(Bx1-Bx0)-(Bx0-Xi[i]))*t*t+4*(Bx0-Xi[i])*t;
      E2x1=E2x1+8*t*t*t*t-16*t*t*t+8*t*t;
      E1y1=E1y1+(-4*(By0-2*By1+By2))*t*t*t*t+4*(-2*(By1-By0)+(By0-2*By1+By2))*t*t*t+4*(2*(By1-By0)-(By0-Yi[i]))*t*t+4*(By0-Yi[i])*t;
      E2y1=E2y1+8*t*t*t*t-16*t*t*t+8*t*t;
    }
    Ex=E1x1/E2x1;
    Ey=E1y1/E2y1;   
    Bx1=Bx1-Ex;
    By1=By1-Ey;    
  } while (Ex*Ex+Ey*Ey>1e-6); // Error ~0.001
  *x1=Bx1;
  *y1=By1;
  
  return;
}

Derivation

Only interesting if you want to do it yourself!

Refactorise B(t):

B(t)=(1-t)^2*B0+2*t*(1-t)*B1+t^2*B2

     =(B0-2*B1+B2)*t^2+2*(B1-B0)*t+B0

Solve Derivatives for e2 with respect to "t":

e2=((Bx0-2*Bx1+Bx2)*t^2+2*(Bx1-Bx0)*t+Bx0-Xi)^2+((By0-2*By1+By2)*t^2+2*(By1-By0)*t+By0-Yi)^2
   =((Bx0-2*Bx1+Bx2)*t^2+2*(Bx1-Bx0)*t+Bx0-Xi)^2
   +((By0-2*By1+By2)*t^2+2*(By1-By0)*t+By0-Yi)^2
   =(Bx0-2*Bx1+Bx2)*(Bx0-2*Bx1+Bx2)*t^4
   +4*(Bx1-Bx0)*(Bx1-Bx0)*t^2
   +  (Bx0-Xi)*(Bx0-Xi)
   +2*(Bx0-2*Bx1+Bx2)*t^2*2*(Bx1-Bx0)*t
   +2*(Bx0-2*Bx1+Bx2)*t^2  *(Bx0-Xi)
   +2*2*(Bx1-Bx0)*t*(Bx0-Xi)
   +...
   =t^4  *(Bx0-2*Bx1+Bx2)*(Bx0-2*Bx1+Bx2)
   +t^2*4*(Bx1-Bx0)*(Bx1-Bx0)
   +      (Bx0-Xi)*(Bx0-Xi)
   +t^3*4*(Bx0-2*Bx1+Bx2)*(Bx1-Bx0)
   +t^2*2*(Bx0-2*Bx1+Bx2)*(Bx0-Xi)
   +t  *4*(Bx1-Bx0)*(Bx0-Xi)
   +...
   =t^4  *(Bx0-2*Bx1+Bx2)*(Bx0-2*Bx1+Bx2)
   +t^3*4*(Bx0-2*Bx1+Bx2)*(Bx1-Bx0)
   +t^2*2*(2*(Bx1-Bx0)*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)*(Bx0-Xi))
   +t  *4*(Bx1-Bx0)*(Bx0-Xi)
   +      (Bx0-Xi)*(Bx0-Xi)
   +...
   =t^4  *(Bx0-2*Bx1+Bx2)*(Bx0-2*Bx1+Bx2)
   +t^3*4*(Bx0-2*Bx1+Bx2)*(Bx1-Bx0)
   +t^2*2*(2*(Bx1-Bx0)*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)*(Bx0-Xi))
   +t  *4*(Bx1-Bx0)*(Bx0-Xi)
   +      (Bx0-Xi)*(Bx0-Xi)
   +t^4  *(By0-2*By1+By2)*(By0-2*By1+By2)
   +t^3*4*(By0-2*By1+By2)*(By1-By0)
   +t^2*2*(2*(By1-By0)*(By1-By0)+(By0-2*By1+By2)*(By0-Yi))
   +t  *4*(By1-By0)*(By0-Yi)
   +      (By0-Yi)*(By0-Yi)

   =t^4  *((Bx0-2*Bx1+Bx2)*(Bx0-2*Bx1+Bx2)+(By0-2*By1+By2)*(By0-2*By1+By2))
   +t^3*4*((Bx0-2*Bx1+Bx2)*(Bx1-Bx0)+(By0-2*By1+By2)*(By1-By0))
   +t^2*2*(2*(Bx1-Bx0)*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)*(Bx0-Xi)+2*(By1-By0)*(By1-By0)+(By0-2*By1+By2)*(By0-Yi))
   +t  *4*((Bx1-Bx0)*(Bx0-Xi)+(By1-By0)*(By0-Yi))
   +      ((Bx0-Xi)*(Bx0-Xi)+(By0-Yi)*(By0-Yi))

   b4=(Bx0-2*Bx1+Bx2)*(Bx0-2*Bx1+Bx2)+(By0-2*By1+By2)*(By0-2*By1+By2)
   b3=(Bx0-2*Bx1+Bx2)*(Bx1-Bx0)+(By0-2*By1+By2)*(By1-By0)
   b2=2*(Bx1-Bx0)*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)*(Bx0-Xi)+2*(By1-By0)*(By1-By0)+(By0-2*By1+By2)*(By0-Yi)
   b1=(Bx1-Bx0)*(Bx0-Xi)+(By1-By0)*(By0-Yi)
   b0=(Bx0-Xi)*(Bx0-Xi)+(By0-Yi)*(By0-Yi)

Summary for Derivatives for e(t) with respect for "t":

   e2(t)=t*t*t*t*b4+4*t*t*t*b3+2*t*t*b2+4*t*b1+b0
   e2'(t)=4*t*t*t*b4+12*t*t*b3+4*t*b2+4*b1
   e2"(t)=12*t*t*b4+24*t*b3+4*b2
   t=t-e2'(t)/e2"(t)

Solve Derivatives with respect to "B1":

   b4(Bx1)=(Bx0-2*Bx1+Bx2)*(Bx0-2*Bx1+Bx2)+(By0-2*By1+By2)*(By0-2*By1+By2)
   b3(Bx1)=(Bx0-2*Bx1+Bx2)*(Bx1-Bx0)+(By0-2*By1+By2)*(By1-By0)
   b2(Bx1)=2*(Bx1-Bx0)*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)*(Bx0-Xi)+2*(By1-By0)*(By1-By0)+(By0-2*By1+By2)*(By0-Yi)
   b1(Bx1)=(Bx1-Bx0)*(Bx0-Xi)+(By1-By0)*(By0-Yi)
   b0(Bx1)=(Bx0-Xi)*(Bx0-Xi)+(By0-Yi)*(By0-Yi)

   b4(Bx1)=(Bx0-2*Bx1+Bx2)*(Bx0-2*Bx1+Bx2)+(By0-2*By1+By2)*(By0-2*By1+By2)
   b4'(Bx1)=2*(Bx0-2*Bx1+Bx2)*(Bx0-2*Bx1+Bx2)'
   b4'(Bx1)=2*(Bx0-2*Bx1+Bx2)*(-2)
   b4'(Bx1)=-4*(Bx0-2*Bx1+Bx2)
   b4"(Bx1)=-4*(-2)
   b4"(Bx1)=8

   b3(Bx1)=(Bx0-2*Bx1+Bx2)*(Bx1-Bx0)+(By0-2*By1+By2)*(By1-By0)
   b3'(Bx1)=(Bx0-2*Bx1+Bx2)'*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)*(Bx1-Bx0)'
   b3'(Bx1)=(-2)*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)*(1)
   b3'(Bx1)=-2*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)
   b3"(Bx1)=-2*(1)+(-2)
   b3"(Bx1)=-4

   b2(Bx1)=2*(Bx1-Bx0)*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)*(Bx0-Xi)+2*(By1-By0)*(By1-By0)+(By0-2*By1+By2)*(By0-Yi)
   b2'(Bx1)=2*(Bx1-Bx0)'*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)'*(Bx0-Xi)+2*(Bx1-Bx0)*(Bx1-Bx0)'+(Bx0-2*Bx1+Bx2)*(Bx0-Xi)'
   b2'(Bx1)=2*(1)*(Bx1-Bx0)+(-2)*(Bx0-Xi)+2*(Bx1-Bx0)*(1)+(Bx0-2*Bx1+Bx2)*(0)
   b2'(Bx1)=2*(Bx1-Bx0)-2*(Bx0-Xi)+2*(Bx1-Bx0)
   b2'(Bx1)=4*(Bx1-Bx0)-2*(Bx0-Xi)
   b2"(Bx1)=4*(1)
   b2"(Bx1)=4

   b1(Bx1)=(Bx1-Bx0)*(Bx0-Xi)+(By1-By0)*(By0-Yi)
   b1'(Bx1)=(1)*(Bx0-Xi)
   b1'(Bx1)=(Bx0-Xi)
   b1"(Bx1)=0

   b0(Bx1)=(Bx0-Xi)*(Bx0-Xi)+(By0-Yi)*(By0-Yi)
   b0'(Bx1)=0
   b0"(Bx1)=0
  
   b4'(Bx1)=-4*(Bx0-2*Bx1+Bx2)
   b4"(Bx1)=8
   b3'(Bx1)=-2*(Bx1-Bx0)+(Bx0-2*Bx1+Bx2)
   b3"(Bx1)=-4
   b2'(Bx1)=4*(Bx1-Bx0)-2*(Bx0-Xi)
   b2"(Bx1)=4
   b1'(Bx1)=(Bx0-Xi)
   b1"(Bx1)=0
   b0'(Bx1)=0
   b0"(Bx1)=0

Summary of derivatives with respect to "B1":

   b4'(By1)=-4*(By0-2*By1+By2)
   b4"(By1)=8
   b3'(By1)=-2*(By1-By0)+(By0-2*By1+By2)
   b3"(By1)=-4
   b2'(By1)=4*(By1-By0)-2*(By0-Yi)
   b2"(By1)=4
   b1'(By1)=(By0-Yi)
   b1"(By1)=0
   b0'(By1)=0
   b0"(By1)=0

   E1x1=Sum(t*t*t*t*b4'(Bx1)+4*t*t*t*b3'(Bx1)+2*t*t*b2'(Bx1)+4*t*b1'(Bx1));
   E2x1=Sum(t*t*t*t*b4"(Bx1)+4*t*t*t*b3"(Bx1)+2*t*t*b2"(Bx1));
   Bx1=Bx1-E1x1/E2x1;

   E1y1=Sum(t*t*t*t*b4'(By1)+4*t*t*t*b3'(By1)+2*t*t*b2'(By1)+4*t*b1'(By1));
   E2y1=Sum(t*t*t*t*b4"(By1)+4*t*t*t*b3"(By1)+2*t*t*b2"(By1));
   By1=By1-E1y1/E2y1;

Non-Suleiman Version

After my last post I realised I did not need Suleiman's code. The Newton-Rapson method could solve the "t" values directly, but it would likely need more iterations.

Here are the results:

So the results are indentical which means my derivation (based on first and second derivates) is but a refactorisation of Suleiman's.

BezierFitV2.c is in the files directory.

Mapping Digitised Points to a Trial Quadratic Bezier Curve

While the quadratic Bezier curve equation is quite simple, it evaded me how to convert a digitised point to the Bezier curve parameter "t".

Upon research I came upon a paper by Nouri A. Suleiman (2013), "Least Squares Data Fitting with Quadratic Bezier Curves".

(source: https://artsakhlib.am/wp-content/uploads/2020/09/Nouri-Suleiman-Least-Squares-Data-Fitting-with-Quadratic-Bezier-Curves.pdf)

Although I did not follow the Least Squares route, the paper presents a method for mapping a digitised point  (i.e. finding the t parameter) to a trial quadratic bezier curve.

For each digitised point Xi[i] and Yi[i], and the trial Bezier curve:

    A*(1-t)^2+2*B*(1-t)*t+C*t*t

Calculate the following (Suleiman) values:

      d0=(Ax-Xi[i])*(Ax-Xi[i])+(Ay-Yi[i])*(Ay-Yi[i]);

      d1=(*Bx-Ax)*(Ax-Xi[i])+(*By-Ay)*(Ay-Yi[i]);

      d2=(Ax-2*(*Bx)+Cx)*(Ax-Xi[i])+2*(*Bx-Ax)*(*Bx-Ax)+(Ay-2*(*By)+Cy)*(Ay-Yi[i])

          +2*(*By-Ay)*(*By-Ay);

      d3=(Ax-2*(*Bx)+Cx)*(*Bx-Ax)+(Ay-2*(*By)+Cy)*(*By-Ay);

      d4=Ax*(Ax-2*(*Bx)+Cx)-2*(*Bx)*(Ax-2*(*Bx)+Cx)+Cx*(Ax-2*(*Bx)+Cx)

          +Ay*(Ay-2*(*By)+Cy)-2*(*By)*(Ay-2*(*By)+Cy)+Cy*(Ay-2*(*By)+Cy);
 

Then calculate the (Suleiman) parameter mapping error:

     e2=d4*t*t*t*t+4*d3*t*t*t+2*d2*t*t+4*d1*t+d0;

Then solve the minimisation problem of e2 for t. We can use the Newton-Raphson method:

     t=t-e2'/e2"

Where:

      e2'=4*(d4*t*t*t+3*d3*t*t+d2*t+d1);
      e2"=4*(3*d4*t*t+6*d3*t+d2);

After finding the trial Bezier curve parameter t for each digitized point, we need to solve the minimisation problem of e2 for Bx of the control point (i.e calculate the first and second derivatives for the sum of e2):

    Sum[e2]=Sum[(Ax*s*s+2*Bx*s*t+Cx*t*t-Xi[i])^2], for each i
    Sum[e2']=Sum[4*s*t*(Ax*s*s+2*Bx*s*t+Cx*t*t-Xi[i])], for each i
                   =Sum[4*(Ax*s*s*s*s+2*Bx*s*s*t*t+Cx*s*t*t*t-Xi[i]*s*t)], for each i
    Sum[e2"]=Sum[8*s*s*t*t], for each i

Then apply Newton-Raphson:
    Bx=Bx-e2'/e2''

Repeat for By.

In the files directory is some C code implimenting the psudo code above.