plotbot

I got myself a nice little linear rail from smalltec.de for 50 bucks:

This will now serve as the z-axis and also provide suspension so that the pen will have more or less constant pressure on the paper. The parts for attaching all the stuff were made from brass strips that I cut down to length, drilled and soldered together with a gas torch:

The large soft spring is for giving the pen pressure on the paper while the small stronger spring is attached to a mini-servo for lifting the pen and was plasticly stretched to allow some movement upwards when the pen is on the paper.
The finished assembly looks like this:

It works great and is very stiff, so much in fact that I noticed how bendy the 1m long arms are, but nevertheless v2 is a big improvement.

I made a simple pen holder out of brass strips, it is a parallelogram with plastic washers as bearings. A tension spring is used to ensure the pen has always contact with the paper, and a mini-servo is used to lift and lower the pen.

While working okayish, unfortunately this design is very wobbly, so I'm making a version 2 based on miniature linear railing.

Motion demo of the plotbot is up and running, it filsl the buffers with timings that have a linear ramp (just a sawtooth-funtion) and moves the arms back and forth with varying speed. Timings for upper and lower stepper are phase-shifted by 180° so that they move in opposite directions. Now here's the video:

Now that the basic firmware functionality is ready, I decided to make the github repo public, so feel free to take a look (if you are not afraid of ugly code).

What works:

• Homing
• Jogging
• Filling the buffers
• Readout information (buffer size, position)
• Make movements from the buffers (need to finish the demo code -> video incoming)
• Basic gui

If you want to try it on hardware, I advise you to just use free spinning motors, because any error in filling the buffers can cause the motors to spin indefinitely.

I decided to pack the electronics on two different boards, one for the microcontroller and one for the motor drivers. Turns out this was a wise move, because I recently switched the motor drivers from A4988's to TMC2209's, specificly SilentStepSticks from Watterott and they are awesome! They are much quieter and I'm quite happy with the stepping speed they offer. I use them in conjunction with Protector Boards, because the power-on is a bit complicated without them.

The controller board looks like this:

There is one big connector to connect the microcontroller with the driver board, and several small connectors for the endswitches.

The driver board looks like this:

The motor drivers get fed by a 24V power supply. A voltage regular is used to generate 5V from the power supply and feed the driver logic and the teensy. The capacitors are necessary to smooth the voltage from the spikes generated by the motors.

As I wrote in the description, I want to write as little code on the microcontroller as possible. Since I learned coding in Python, programming in C/C++ just feels tedious and I want to minimize it. So the idea was to do all complicated calculations in language that I like more, like Python or Nim (which is awesome!).

As far as my understanding goes, usually gcode is sent to the microcontroller, which uses some variation of Bresenhams algorithm to calculate the timings for the stepper motors.

My Idea is to instead calculate all the timings on the computer and send them to the microcontroller which stores them in a buffer and uses a timer to step the motors. For this, one needs fast serial connection and this is one reason why I chose to use a teensy for this project.

The communication protocol for filling the buffer of the microcontroller with n timings looks like this:

So there are two buffers, one for either stepper, that get filled independently. And the buffers hold the time in seconds until the next step should be done and some action that should be done at that point in time.

The unusual geometry of plotbot means that one has to find a way to map the Cartesian coordinates of what shall be drawn to the coordinates of the steppers in a way that the tip of the triangle that is formed by the arms will follow the Cartesian coordinates of the drawing. In the first Log I made a python script that shows how to do that transformation if you want to go from stepper coordinates to drawing/tip coordinates. But to drive the steppers one has to calculate the transformation the other way around, which has given me some headaches but in the following I'll show how I solved that problem.

First some definitions:

• x and y denote coordinates in tip/drawing space, meaning x and y are the coordinates of a point in the plane of the drawing

• a and b denote coordinates in stepper space, meaning that a and b are coordinates in a hypothetical plane which is defined by the steps of the stepper motors, but they can easily be expressed in tip space:

With d being the distance between the rails.

I could not  figure out how to go the reverse way from what I did in the first Log but there is another way to calculate the tip position from the stepper coordinates:

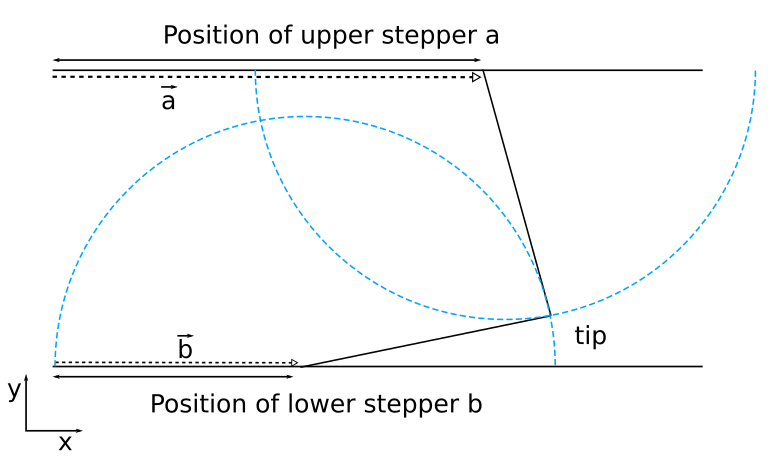
So if we want to calculate the position of the tip we can simply calculate the position of the tip we can simply calculate the intersections of the the two circles centered at position (a, d) and (b, 0) with a radius that equals the length of the arms and choose the rightmost intersection as the solution.

Now this is easily reversed:

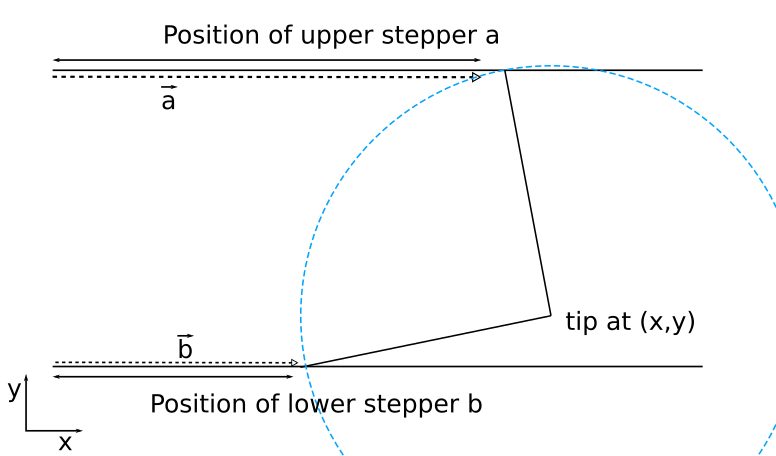
If we know the position of the tip (x,y) we can calculate the intersections of the circle centered at (x,y) with a radius that equals the length of the arms and the lines defined by the upper and lower rail. Now we choose the leftmost solutions and have our coordinates a and b, that define a point in stepper space (a,b).

So that is pretty neat, but there is one more thing to know: These transformations are far from linear, that means they can't be reproduced just by a set of simple translations, rotations or a squeezing/unsqueezing of the length-scales.

This haunted me while programming the control-software, and I will show the implications of this in a later log.

Now that the Project has successfully ripened, it is time to make some progress!

So I made a simple frame from wood (2.5cm x 9cm):

The frame is just glued using simple tongue and groove joints:

The grooves were cut with a router, and the tongues were cut with a band-saw. Then I just glued a 3mm three-layer-board on top.

Next I assembled all the parts that gathered dust for the last years:

The frame is 2m x 1m, which I realize now is a bit over the top, but you've got to give your megalomania a treat sometimes I guess.

Right now I'm working on the software and I probably there will be more updates in the next weeks.

To check if the geometry is ok I wrote a little python script to calculate the area which the plotter arms can acces:

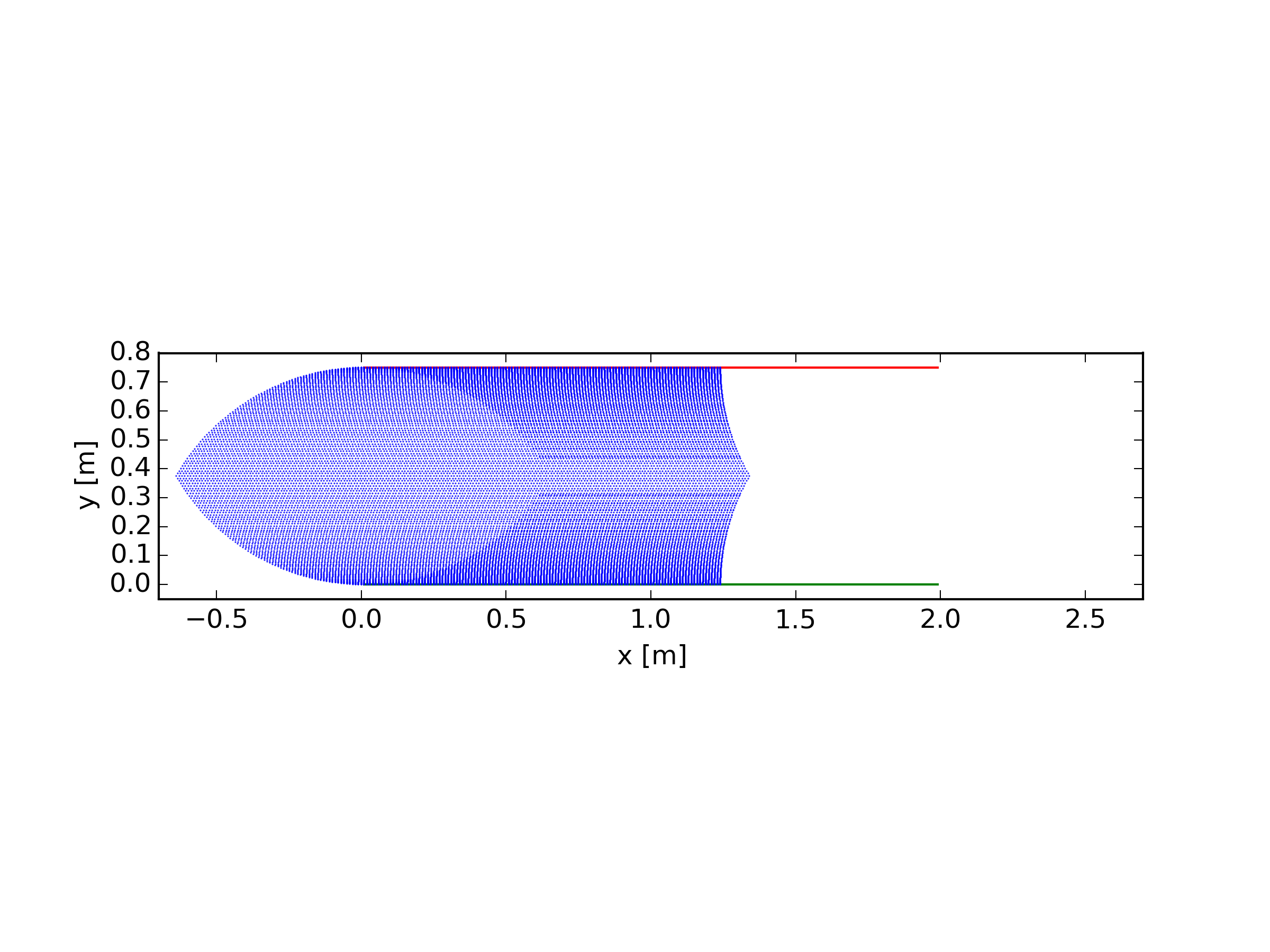
import math
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
from planar import Vec2

al = 0.75 #arm length [m]
f = 0.75 #position of rail a [m] 

apos = [2 * x * 0.005 for x in range(1, 200)]
bpos = [2 * x * 0.005 for x in range(1, 200)]

cx = []
cy = []

for x_a in apos:
    for x_b in bpos:
        a = Vec2(x_a,f) # vector to position on arm a
        b = Vec2(x_b,0) # vector to position on arm b

        cl = (b-a).length #distance between a and b

        #calculate height of triangle which is spanned by the arms
        hl = 2*((al**2)*(al**2)+(al**2)*(cl**2)+(cl**2)*(al**2))-(al**4+al**4+cl**4)

        if hl > 0:
            # finish calculation of height
            hl = math.sqrt(hl)/(2*cl)

            #vector from a to b
            d = (b-a)
            d = d/d.length

            # turn d around by 90°, h points to tip of triangle
            h = Vec2(d.y,-d.x)

            # normalize h
            h = h/h.length

            # calculate distance to tip set as length of d
            d *= math.sqrt(al ** 2 - hl ** 2)

            # vector which points to the tip of the triangle
            c = a+d+h*hl

            #save coordinates of tip
            cx.append(c.x)
            cy.append(c.y)

plt.plot([min(apos),max(apos)],[f,f],'r')
plt.plot([min(bpos),max(bpos)],[0,0],'g')
ax = plt.gca()

points = plt.plot(cx,cy,'o')
plt.setp(points,'color', 'b', 'marker', '.', 'markersize', 0.5)

plt.axes().set_aspect('equal')

plt.xlim([-0.7,2.7])
plt.ylim([-0.05,0.8])
plt.xlabel('x [m]')
plt.ylabel('y [m]')
plt.show()

Running the script gives the following plot:

The blue area is what the plotter can reach, the density of the dots is a measure for the resolution. Luckily the density is pretty homogenious, so the resolution of the plotter will be more or less constant over the whole drawin area.

Also one might wonder what with the empty space on the right, I'll show that in a follow up.

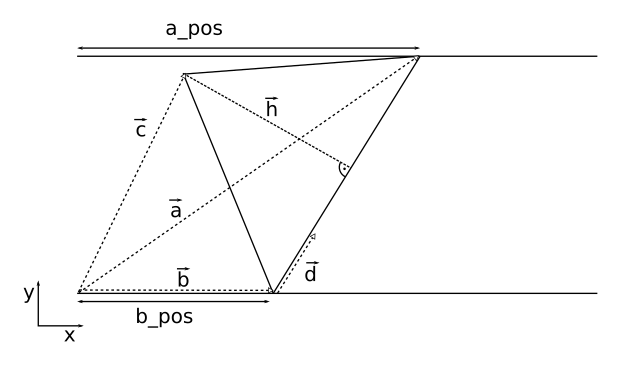
Here's also a little sketch which shows what the calculations in the script are based on: