-
And one more thing II
01/08/2022 at 11:48 • 7 commentsYann pointed out in a comment that a Johnson counter may be a good way to save some gates in the logic implementation of the dice. Currently a simple binary counter is used.
To be honest, it seems that I mistakenly thought of Johnson counters being simple ring counter with one flipflop per state, when in fact they are a nice concept to reduce the number of flipflops needed for a counter by two compary to a ring counter. Even the Wikipedia entry throws Johnson counter and ring counters into one category, which is a bit confusing.A fairly nice property of a Johnson counter implementation is that it is possible to implement a counter that comes with a natural sequence length of 6, exactly what we need for the dice. So, in contrast to the binary counter, no additional logic is needed to limit the sequence length.
Some caveats
- The sequence is not in order, since it does not follow binary encoding
- The sequence contains "000", which is currently not decoded as a valid face figure on the die.
- There are illegal states of the counter, so it has to be initialized
1) is not really an issue, since we want to randmize the die anyways. So we just accept that the sequence is different. 2) can be solved by inverting the middle bit. See below. 3) requires is to add a reset input. But the NE555 comes with a reset input anyways, so that is almost for free.
Sequence johnson counter middle bit inverted dice pattern Seq1 000 010 2 Seq2 001 011 3 Seq3 011 001 1 Seq4 111 101 5 Seq5 110 100 4 Seq6 100 110 6Here comes the VHDL implementation of the modified dice:
architecture main of dice555johnson is signal cnt: unsigned(2 downto 0); begin process (clk,n_clk,nreset) begin if nreset = '0' then cnt <= "000"; elsif rising_edge(clk) then cnt <= cnt(1 downto 0) & NOT cnt(2); end if; end process; -- 1 2 -- 3 0 3 -- 2 1 -- Encoding: -- 011 0 -- 000 1 -- 001 0,1 -- 110 1,2 -- 111 0,1,2 -- 100 1,2,3 -- drive inverted LEDs dice(0) <= NOT cnt(0); dice(1) <= '1' when (cnt = "011") else '0'; dice(2) <= NOT cnt(2); dice(3) <= '0' when (cnt = "100") else '1'; end;And here are the design stats after synthesis:
Number of cells: 9 ne_DFF_clear 3 ne_NAND3 2 ne_NOT 4 Chip area for module '\main': 23.000000Spice netlist
.SUBCKT main clk n_clk nrst dice.0 dice.1 dice.2 dice.3 X0 cnt.1 1 ne_NOT X1 cnt.2 dice.2 ne_NOT X2 cnt.0 dice.0 ne_NOT X3 1 cnt.2 dice.0 dice.3 ne_NAND3 X4 cnt.1 dice.2 cnt.0 2 ne_NAND3 X5 2 dice.1 ne_NOT X6 clk nrst dice.2 cnt.0 ne_DFF_clear X7 clk nrst cnt.0 cnt.1 ne_DFF_clear X8 clk nrst cnt.1 cnt.2 ne_DFF_clear .ENDS mainCompared to the stats of the original implementation with binary counter:
Number of cells: 18 ne_DFF 3 ne_NAND2 7 ne_NAND3 2 ne_NOT 6 Chip area for module '\main': 39.000000Quite impressive! Thanks for the tip, Yann. Will I build this? Probably not, I trust that it would work and I think owning one NE555 based electronic dice is already enough :)
Edit: Digital simulation output is shown below. Please note, that the dice output is inverted since the LEDs are active low. I found a tiny bug, which is fixed above.
-
Validating Actual Hardware
01/02/2022 at 04:05 • 0 commentsThe PCB in all its glory
![]()
![]()
Validation
First step is to test the clock generation. The scope image below shows how the CD4017 generates the nonoverlapping two phase clock (clk and clk_n) from the input clock signal. It appears that the CD4017 is able to operate only up to ~1.3 MHz, so maximum generated output clock is around 300 kHz. This is not a big issue since this is still far beyond the capabilities of NE555 logic.
Unfortunately, things did not go as smoothly from there. After some debugging I found that I had to raise the operating voltage to 6V for the dice to function properly. The reason for that is the loading of the clock nets when the input to the latches is low. In that case, the output of the CD4017 has to drive a VBE-diode and a 3.3kohm resistor vs ground. Apparently this is too much and we can observe a significant drop in output voltage which which does not allow the NE555 flip flop to switch. (See here for the latch design)
This is apparant in the scope image below where the high level of the clock signal varies depending on state of the dice.Apart from raising the voltage, another fix would be to increase the base resistor value of the pass-gate devices in the latch or introducing some NE555 as clock drivers. Of course, a much cleaner way would be to construct latches from diodes and NE555 like mike has done in his project. But this would raise the number of NE555 further.
Dice action!
All said and done, see below for a short clip of the dice operating in NE555 logic!
![]()
And another logic type proven in practice! Would I use it for other designs? Probably not. The area consumption is huge, cost is quite high, power consumption is higher than even RTL (~70 mA for the dice) and it is by far the slowest logic type I ever investigated.
Unfortunately the version I built based on ANDN2 gates does not seem to work properly. Some more debugging is needed to figure out the root cause.
-
One more thing: NE555 ANDN2 Logic
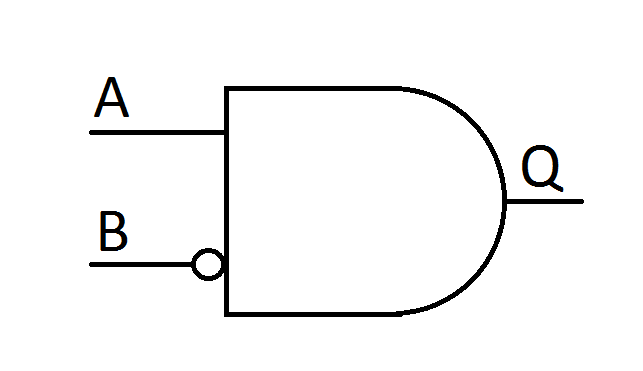
12/20/2021 at 23:04 • 0 commentsI was made aware of Erics earlier work on NE555 based logic. He actually came up with a pretty neat trick to turn the NE555 into more than just a boring inverter by also using the reset input of the NE555. This results in a logic function based on an AND-gate with one inverted input:
![A_AND_NOT_B]()
Image taken from Erics article linked above The naming of this type of gate is debatable, but I call it "ANDN2" in my library. It is actually fairly easy to implement this gate in PCBflow as well. I made a version of the dice where I enforced the AND2 and NOT gate to be the only type of logic gate being used:
Number of cells: 19 ne_ANDN2 10 ne_DFF 3 ne_NOT 6 Chip area for module '\main': 31.000000Turns out the area is even smaller than withe the Diode/NE555 gates I used before. The reason for that is that no additional space is needed for diodes.
Unfortunately I had a lot of trouble simulating this logic style with spice. So instead of debugging issues with operating point I decided to take the pragmatic way and turn this into a board to test it rather in hardware. A rendering of the board is shown below. (I miss-spellt the gate type on the silk screen).
=== Component usage === Component Count pin 8 NE555 22 cap 22 npn transistor 6 resistor 18 ------------------ ----- Total: 76This logic style requires a slightly higher count of NE555, 22 instead of 21. Not a bad trade-off, because many diodes are saved.
I should be able to test both versions in about two weeks.
-
Placement and PCB Layout
12/20/2021 at 22:40 • 0 commentsNow that the design topics have been fixed and the circuit works in simulation, we can continue to generate a layout. Again, using PCBflow will output a preliminary PCB with placed components:
The statistics are as follows:
Microcell counts: ne_NOT 21 ne_WAND2 7 ne_TBUF 6 ne_WAND3 2Component usage
Component Count pin 8 NE555 21 cap 21 resistor 27 diode 20 npn transistor 6 ------------------ ----- Total: 103Well, i'd say it's a bit more than a dice with the old role-models of NE555 and CD4017 require, but who are we to judge? Still small enough to comfortably build and test.
Still some work to do manually: Add the LEDs for the dice, add the CD4017 clock generator footprint, add groundplane and let the autoroute do its (admittedly gut-wrenching) job.
And here we are, with a nice simulation of the full PCB. A modern rendition of the classic NE555/CD4017 based electronic dice.
PCBs are being made now and should arrive soon.
-
Finally a use for the CD4017: A clock generator
12/20/2021 at 22:34 • 0 commentsWell, now that the job of the CD4017 in the dice is taken by the NE555, what can we do with the CD4017? Indeed, there is a perfect match for using it has a generator for the two non-overlapping clocks:
The circuit above will convert a single clock signals into two non-overlapping clocks. Exactly as needed for the NE555 logic. A simulation of this circuit is shown below. The signal in the lower row is the clock input.
Things are coming together nicely...
-
Simulating the circuit and introducing a two phase clock
12/20/2021 at 22:31 • 0 commentsSo far, so good. Unfortunately I ran into some issues here, as the circuit proved quite glitchy during spice simulation. A lot of digging revealed that the setup and hold times of the NE555 latches were somewhat unpredicatable due to the slow speed and under some circumstances the register was not updated during a clock cycle. Each register is implemented by a master-slave flip-flop and simply using an normal and inverted clock signal proved to be unreliable.
In the end I managed to fix this by introducing a non-overlapping two phase clock, driving master and slave latch of each register separately. The simulation below shows the functionality of the dice, cycling through all six die patterns. The two clock signals (clk and n_clk) are shown at the bottom
-
The Design
12/20/2021 at 22:26 • 0 commentsBringing the NE555 into the future also means using modern tools. We'll describe the functionality of the dice in VHDL and use PCBFlow to synthesize the digital description into an implementation based on NE555 logic.
At the same time this will also be the first "real life" test of NE555 logic, as the MCPU is a bit too complex and large to detect basic errors with the logic style.
---------- more ----------library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; -- 1 2 -- 3 0 3 -- 2 1 -- Encoding: -- 001 1 -- 010 2 -- 011 1,2 -- 100 2,3 -- 101 1,2,3 -- 110 2,3,4 entity dice555 is port (clk: in std_logic; n_clk: in std_logic; dice: out std_logic_vector(3 downto 0) ); end; architecture main of dice555 is signal cnt: unsigned(2 downto 0); begin process (clk,n_clk) begin if rising_edge(clk) then if cnt < 6 then cnt <= cnt + 1; else cnt <= "001"; end if; end if; end process; -- drive inverted LEDs dice(0) <= NOT cnt(0); dice(1) <= '1' when (cnt = "001") else '0'; dice(2) <= NOT cnt(2); dice(3) <= '0' when (cnt = "11X") else '1'; end;The VHDL source of the dice is shown above. Basically it consists of a counter, counting from 1 to 6 and repeating, and an encoder for the dice pattern.
The encoder has 4 outputs, dice.0 to dice.3, which are assigned as in the picture above. The plan is to connect the LEDs from VCC to ground, to utilize the better driving capability of the lower side NPN. Therefore the pattern encoding is inverted.
Output after the synthesis step below. Around 21 NE555 are needed to implement the dice circuit.Number of cells: 18 ne_DFF 3 ne_NAND2 7 ne_NAND3 2 ne_NOT 6 Chip area for module '\main': 39.000000Logic after synthesis:
And the spice output after techmapping to the NE555 logic library:
.SUBCKT main clk n_clk dice.0 dice.1 dice.2 dice.3 X0 cnt.0 dice.0 ne_NOT X1 cnt.2 dice.2 ne_NOT X2 cnt.1 1 ne_NOT X3 cnt.2 cnt.1 dice.3 ne_NAND2 X4 cnt.0 dice.3 2 ne_NAND2 X5 dice.0 cnt.1 3 ne_NAND2 X6 dice.2 1 4 ne_NAND2 X7 dice.3 3 4 5 ne_NAND3 X8 5 6 ne_NOT X9 cnt.0 1 7 ne_NAND2 X10 3 7 8 ne_NAND2 X11 dice.3 8 9 ne_NAND2 X12 9 10 ne_NOT X13 cnt.0 dice.2 1 11 ne_NAND3 X14 11 dice.1 ne_NOT X15 clk 6 cnt.2 ne_DFF X16 clk 2 cnt.0 ne_DFF X17 clk 10 cnt.1 ne_DFF .ENDS main
 Tim
Tim



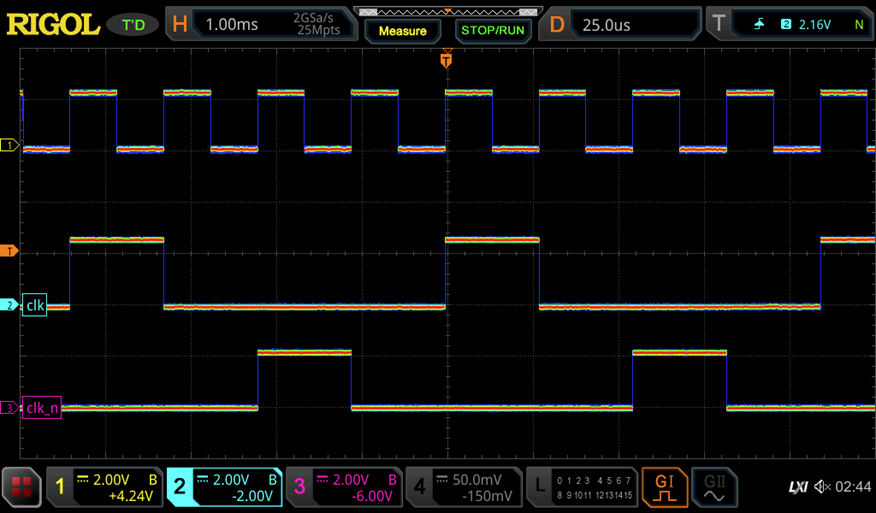 Unfortunately, things did not go as smoothly from there. After some debugging I found that I had to raise the operating voltage to 6V for the dice to function properly. The reason for that is the loading of the clock nets when the input to the latches is low. In that case, the output of the CD4017 has to drive a VBE-diode and a 3.3kohm resistor vs ground. Apparently this is too much and we can observe a significant drop in output voltage which which does not allow the NE555 flip flop to switch. (See
Unfortunately, things did not go as smoothly from there. After some debugging I found that I had to raise the operating voltage to 6V for the dice to function properly. The reason for that is the loading of the clock nets when the input to the latches is low. In that case, the output of the CD4017 has to drive a VBE-diode and a 3.3kohm resistor vs ground. Apparently this is too much and we can observe a significant drop in output voltage which which does not allow the NE555 flip flop to switch. (See 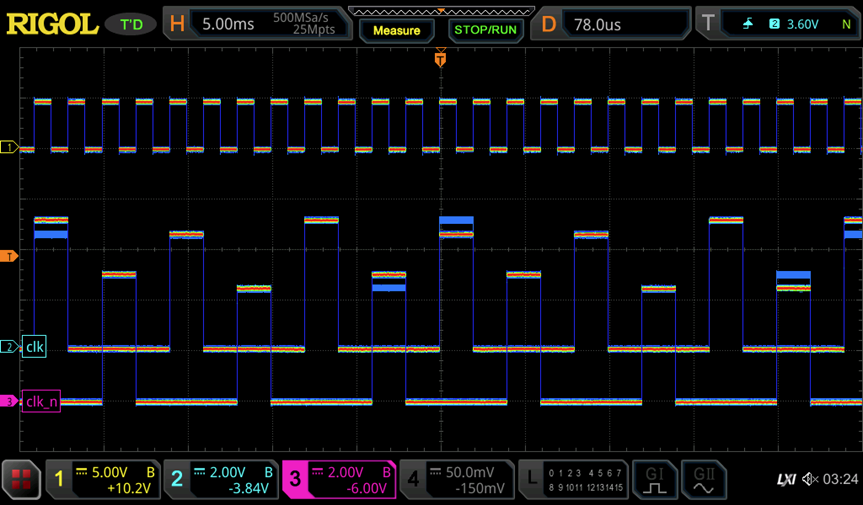


 The statistics are as follows:
The statistics are as follows: PCBs are being made now and should arrive soon.
PCBs are being made now and should arrive soon.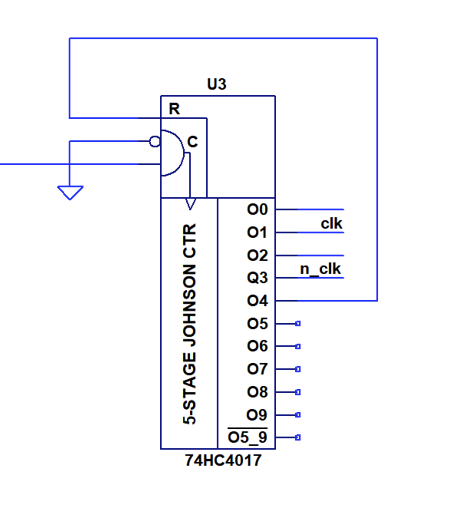 The circuit above will convert a single clock signals into two non-overlapping clocks. Exactly as needed for the NE555 logic. A simulation of this circuit is shown below. The signal in the lower row is the clock input.
The circuit above will convert a single clock signals into two non-overlapping clocks. Exactly as needed for the NE555 logic. A simulation of this circuit is shown below. The signal in the lower row is the clock input.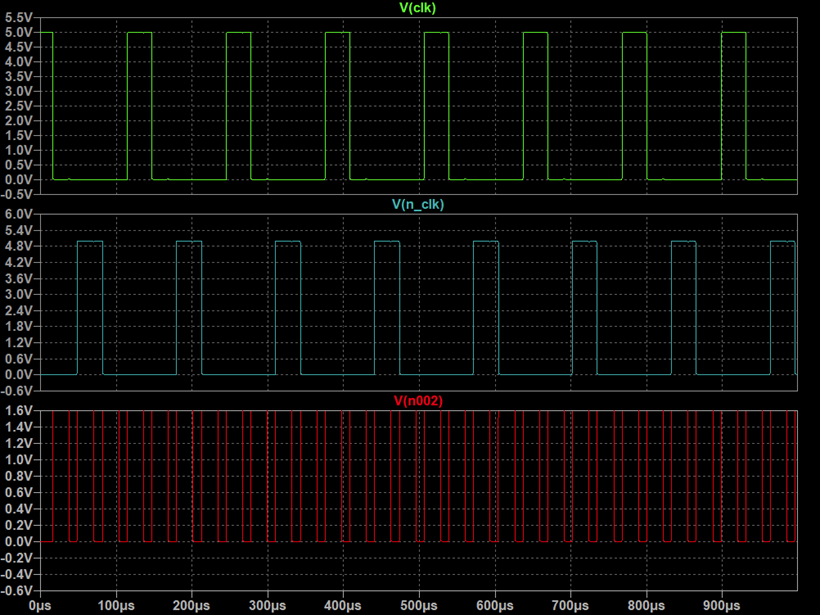 Things are coming together nicely...
Things are coming together nicely...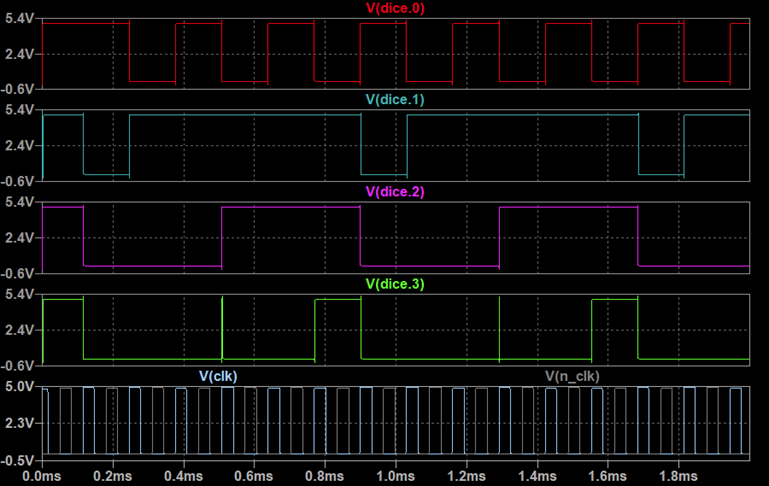
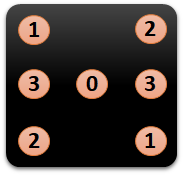
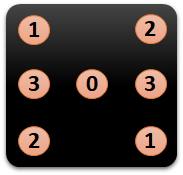 The encoder has 4 outputs, dice.0 to dice.3, which are assigned as in the picture above. The plan is to connect the LEDs from VCC to ground, to utilize the better driving capability of the lower side NPN. Therefore the pattern encoding is inverted.
The encoder has 4 outputs, dice.0 to dice.3, which are assigned as in the picture above. The plan is to connect the LEDs from VCC to ground, to utilize the better driving capability of the lower side NPN. Therefore the pattern encoding is inverted.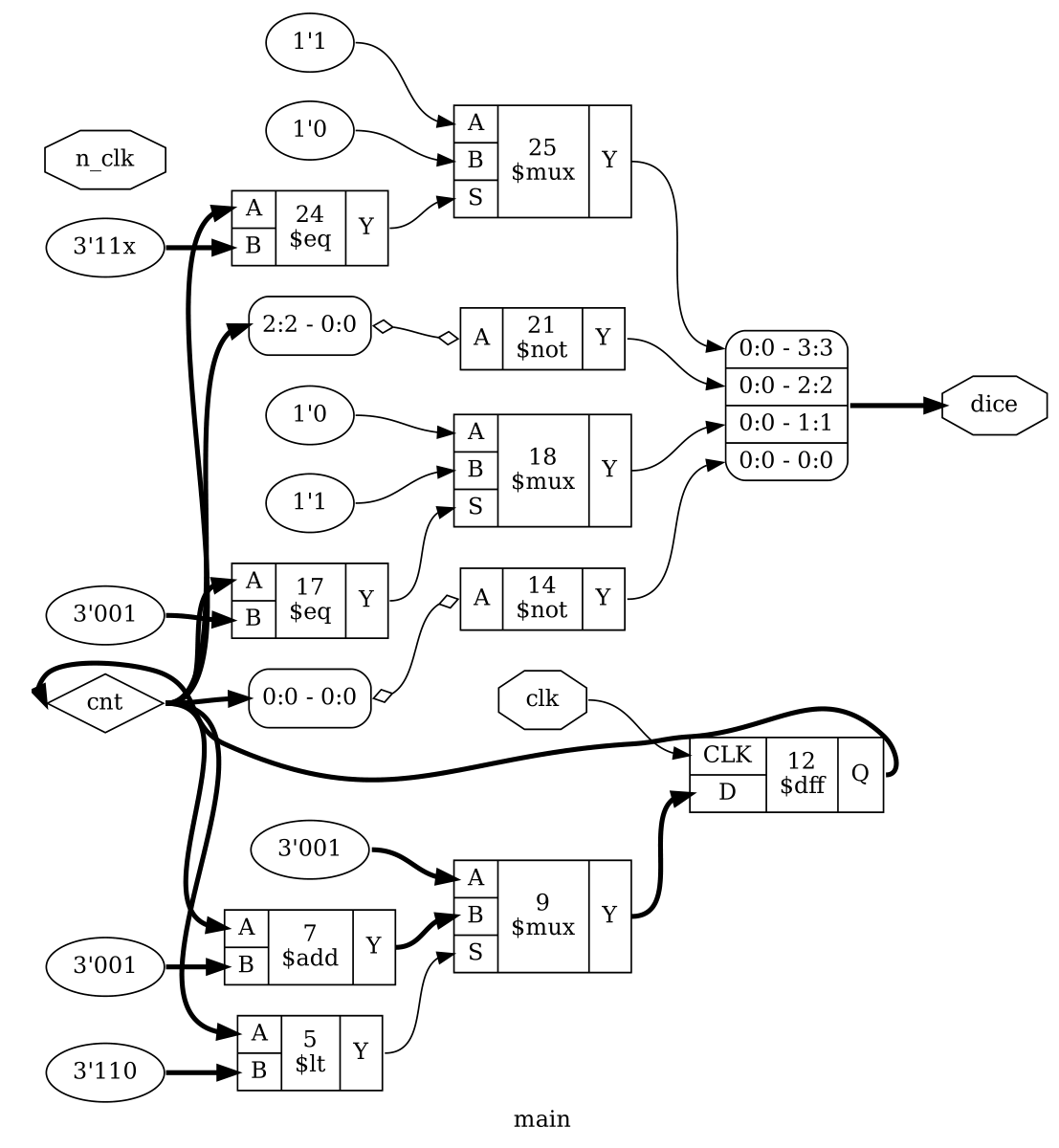 And the spice output after techmapping to the NE555 logic library:
And the spice output after techmapping to the NE555 logic library: