Standing waves occur when two waves (e.g. sound, light, water) of the same wavelength move through each other in opposite directions. This results in a characteristic pattern of nodes and anti-nodes, corresponding to zero and maximum wave amplitude. In an unconstrained system, standing waves could be observed at any wavelength. But usually systems are constrained in space, for example the guitar string is forced to have a node of zero vibration amplitude at either end, where the string runs out. In this case this leads to standing waves of only certain wavelengths, the ones that have a node at each end, giving the musical result that we all like.
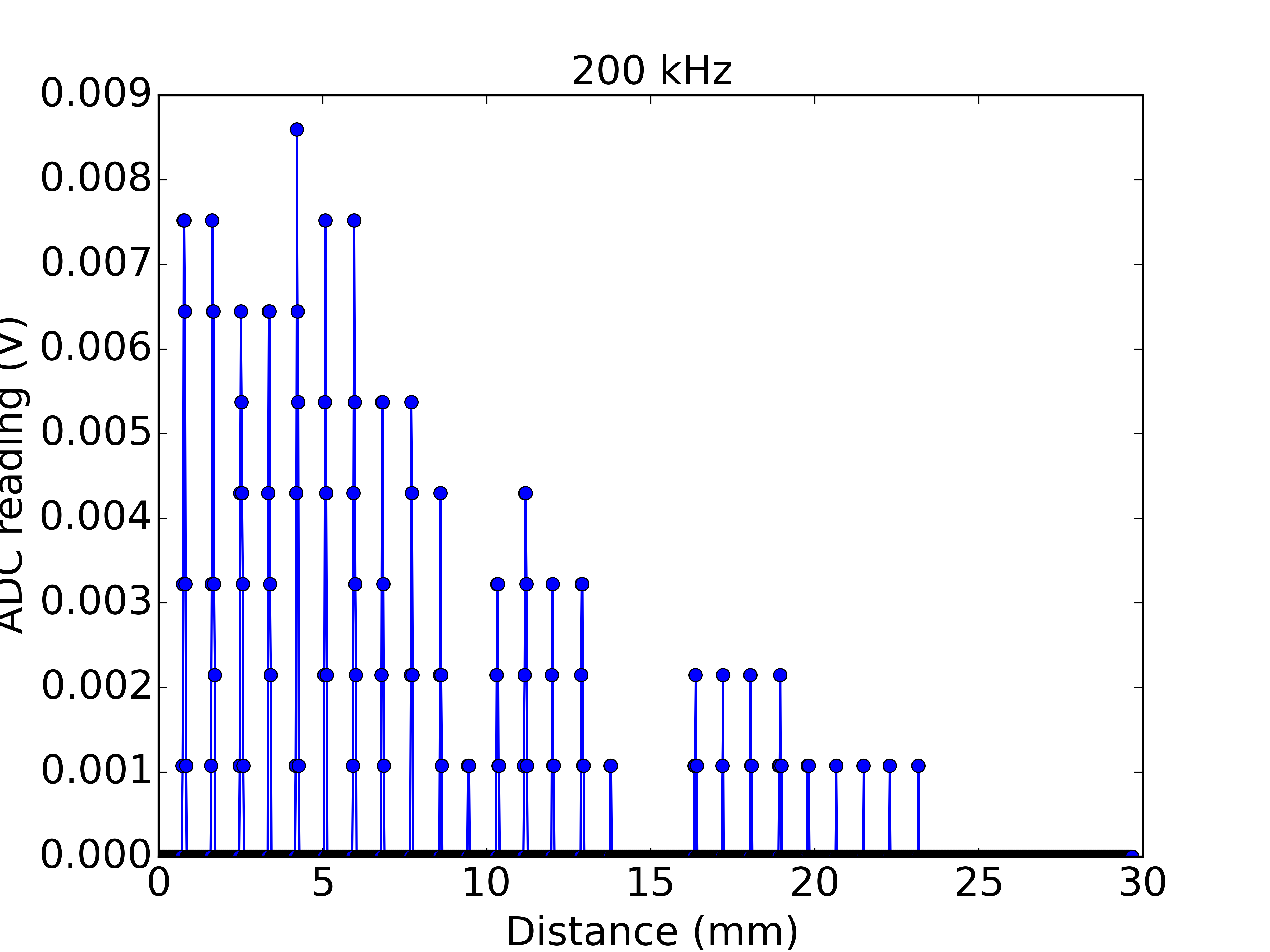
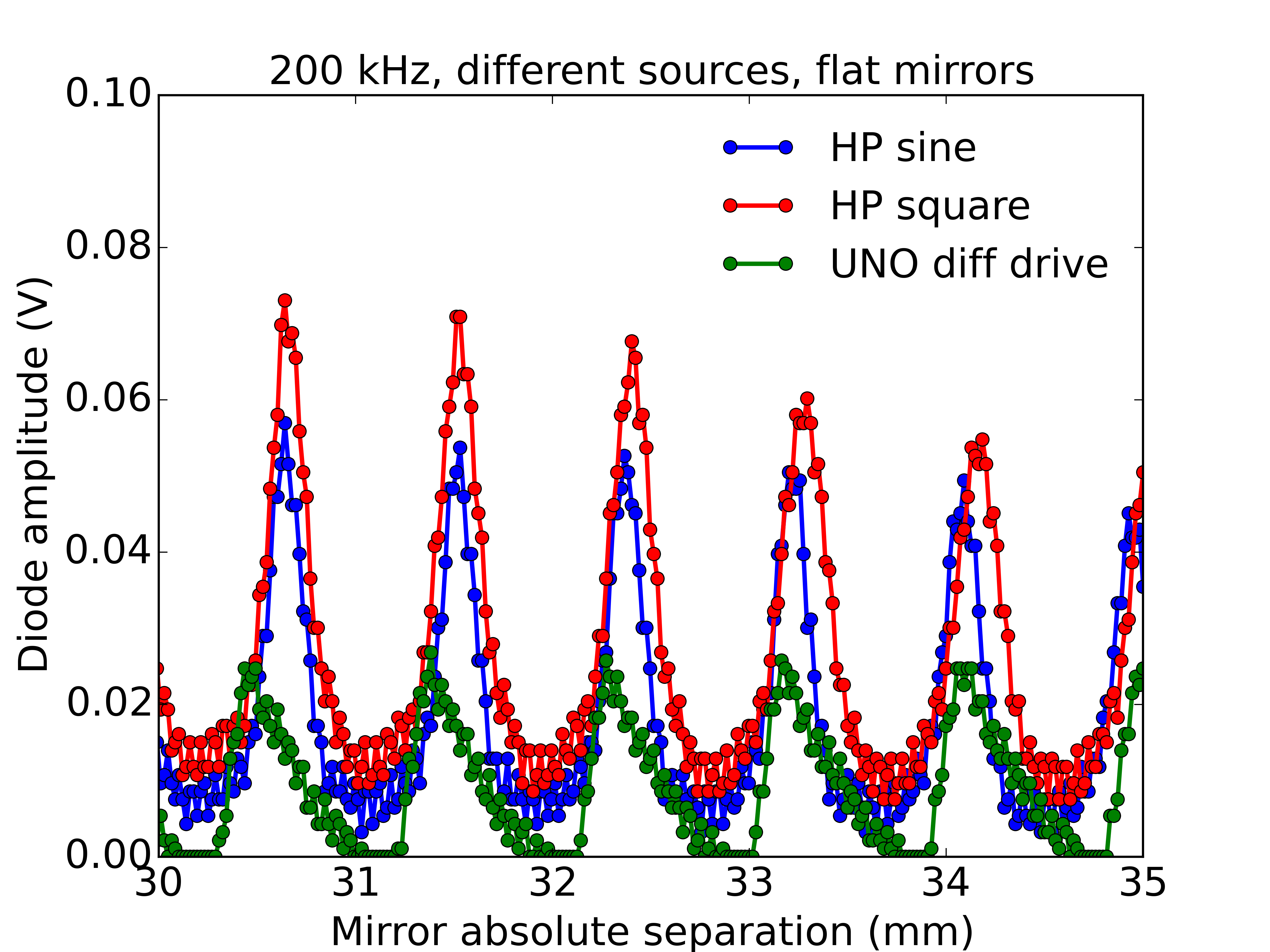
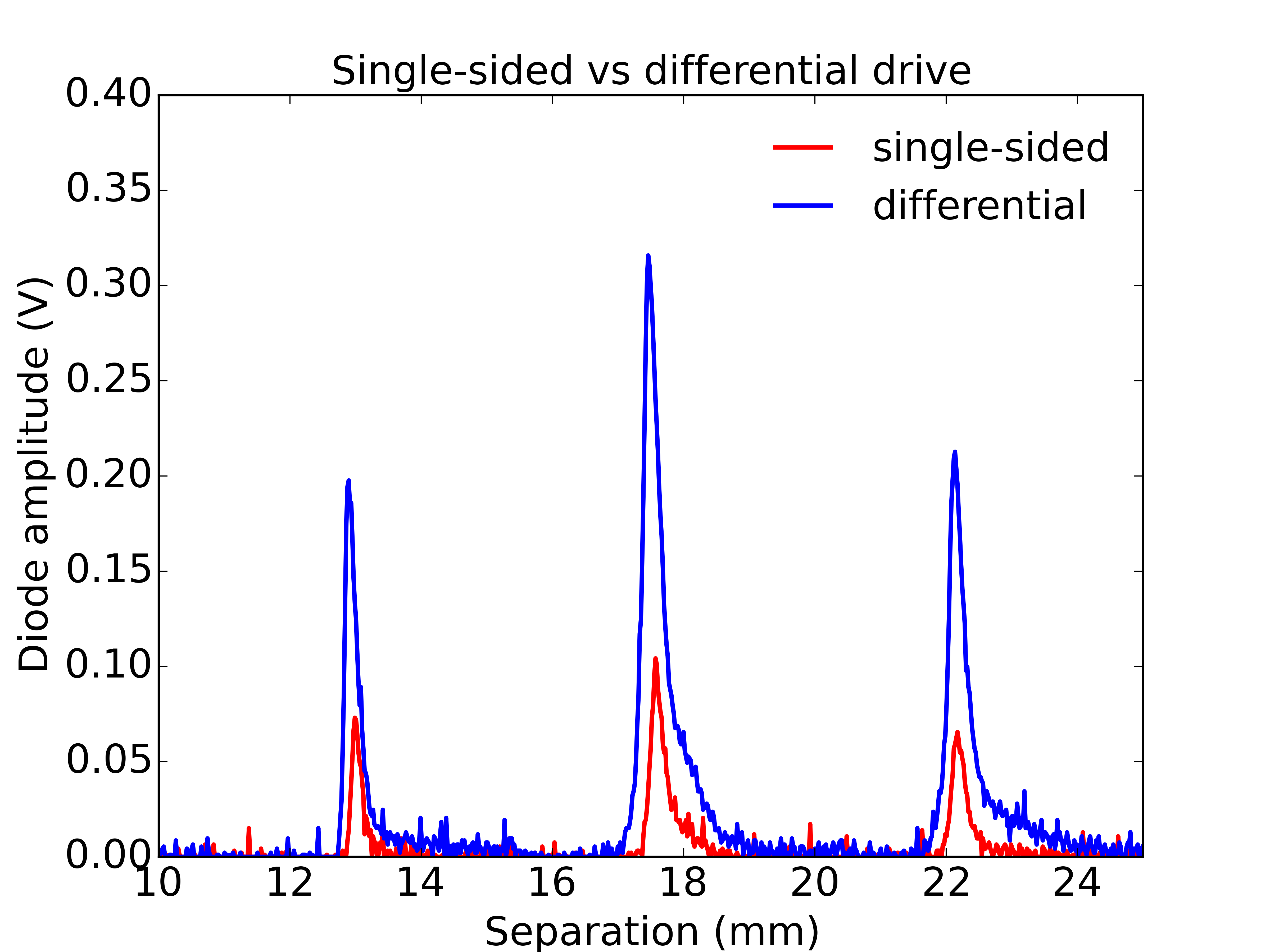
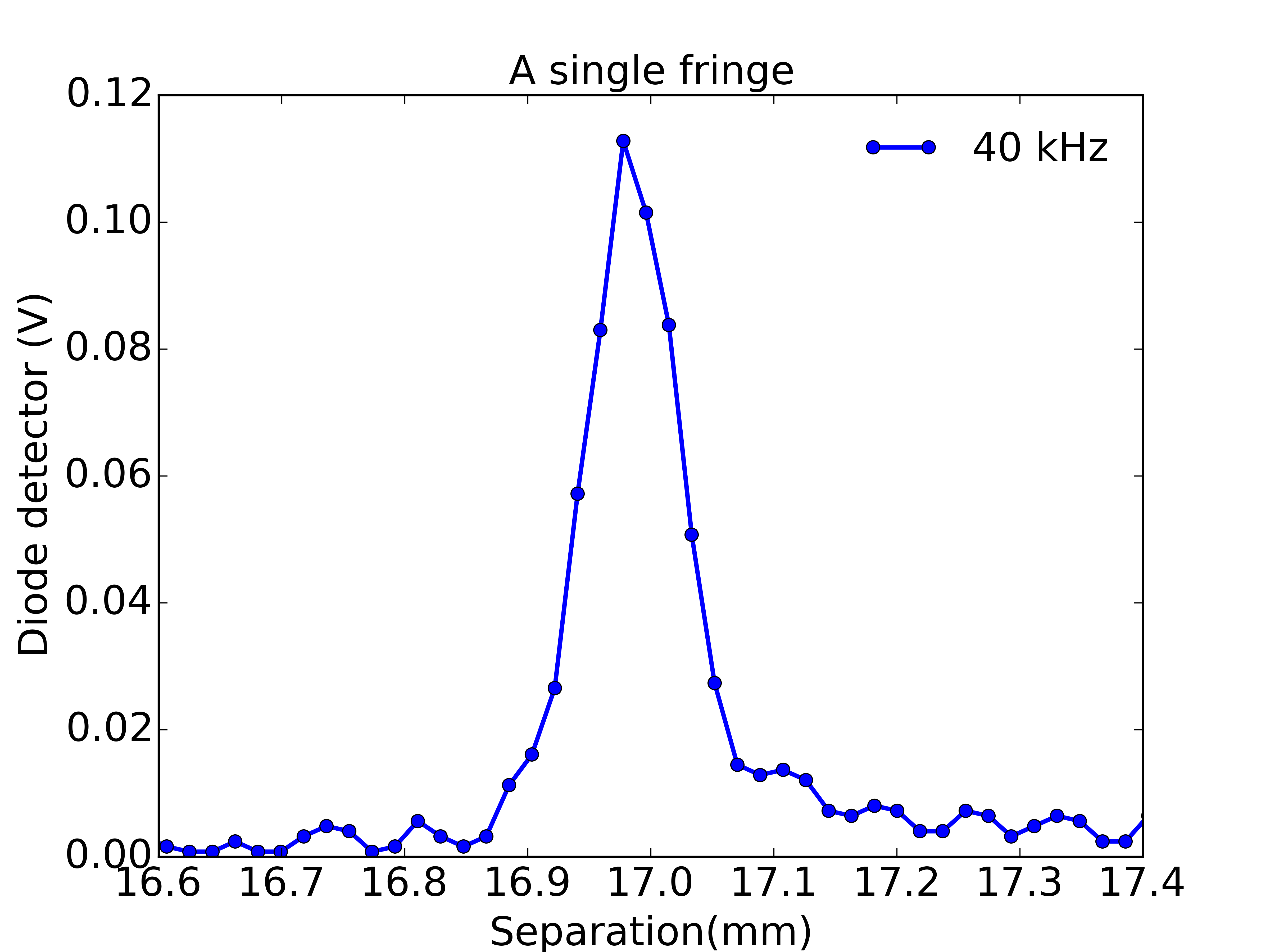
A useful case of standing waves occurs in optics with the Fabry-Perot spectrometer. This consists of two partially transmitting mirrors with their reflecting faces parallel and held apart by some separation. A standing wave pattern is permitted if the separation is an integer multiple of half wavelengths. In this case the system is constrained to have zero amplitude of electromagnetic field at the mirrors, which are just like the ends of the guitar string. It turns out that when this standing wave condition is satisfied then there is a maximum in transmission through the mirrors. The separation of the mirrors can be varied, and extremely sharp peaks in transmission are found around the standing wave conditions. The sharpness of these peaks allows this device to act as a spectrometer, as the distance between mirrors is scanned it becomes a controllable bandpass filter for light.
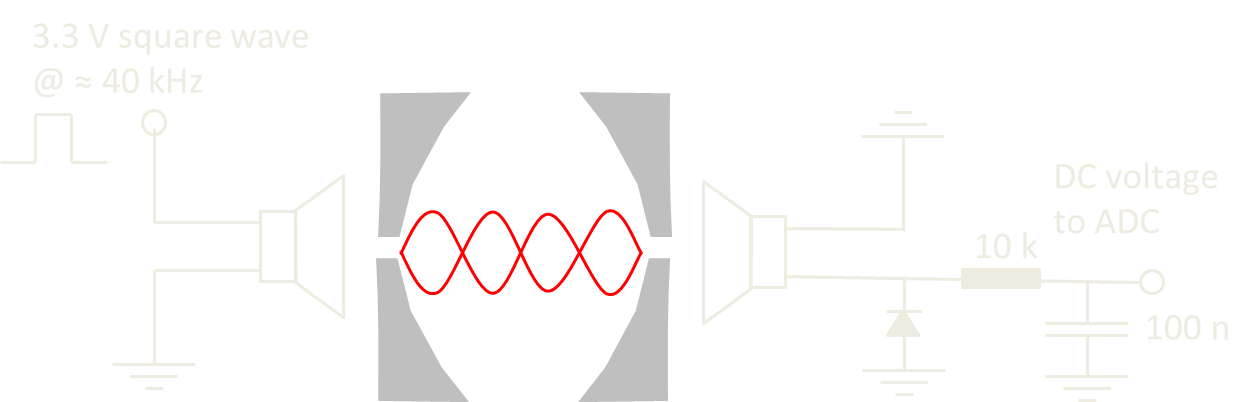
I thought it would be fun to play with a Fabry-Perot but they are a little tricky to setup at home so I decided to replicate the experiment with sound waves. In itself this is not going to provide a useful scientific instrument but it does provide an exact analogy to the optical case and lets us learn the physics behind this precision spectroscopy technique.
 Andrew Ferguson
Andrew Ferguson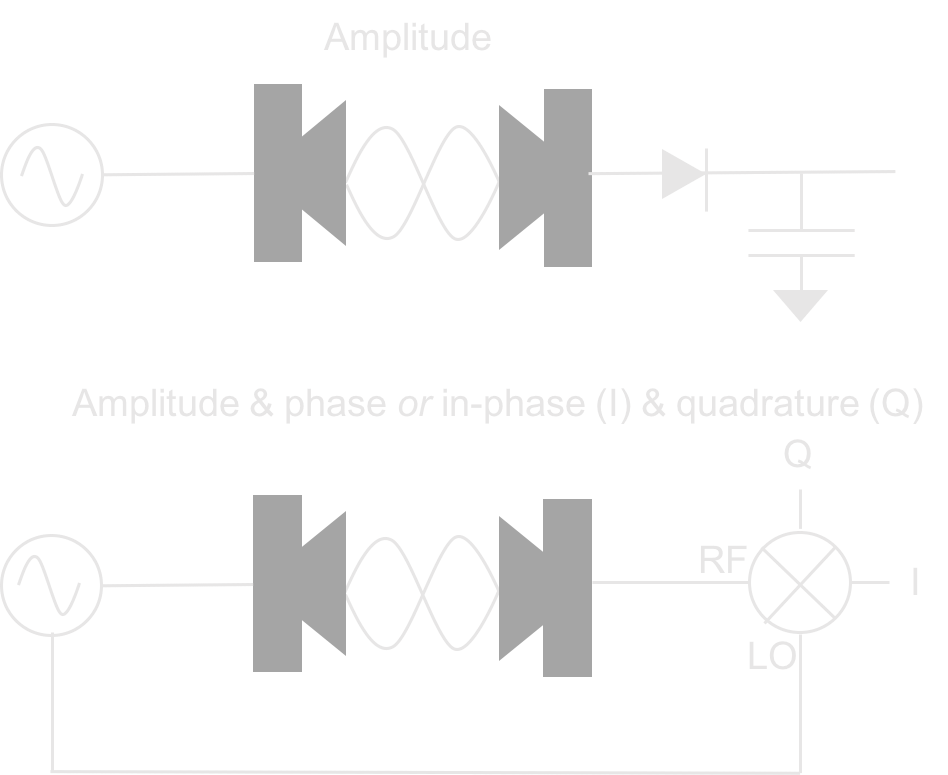


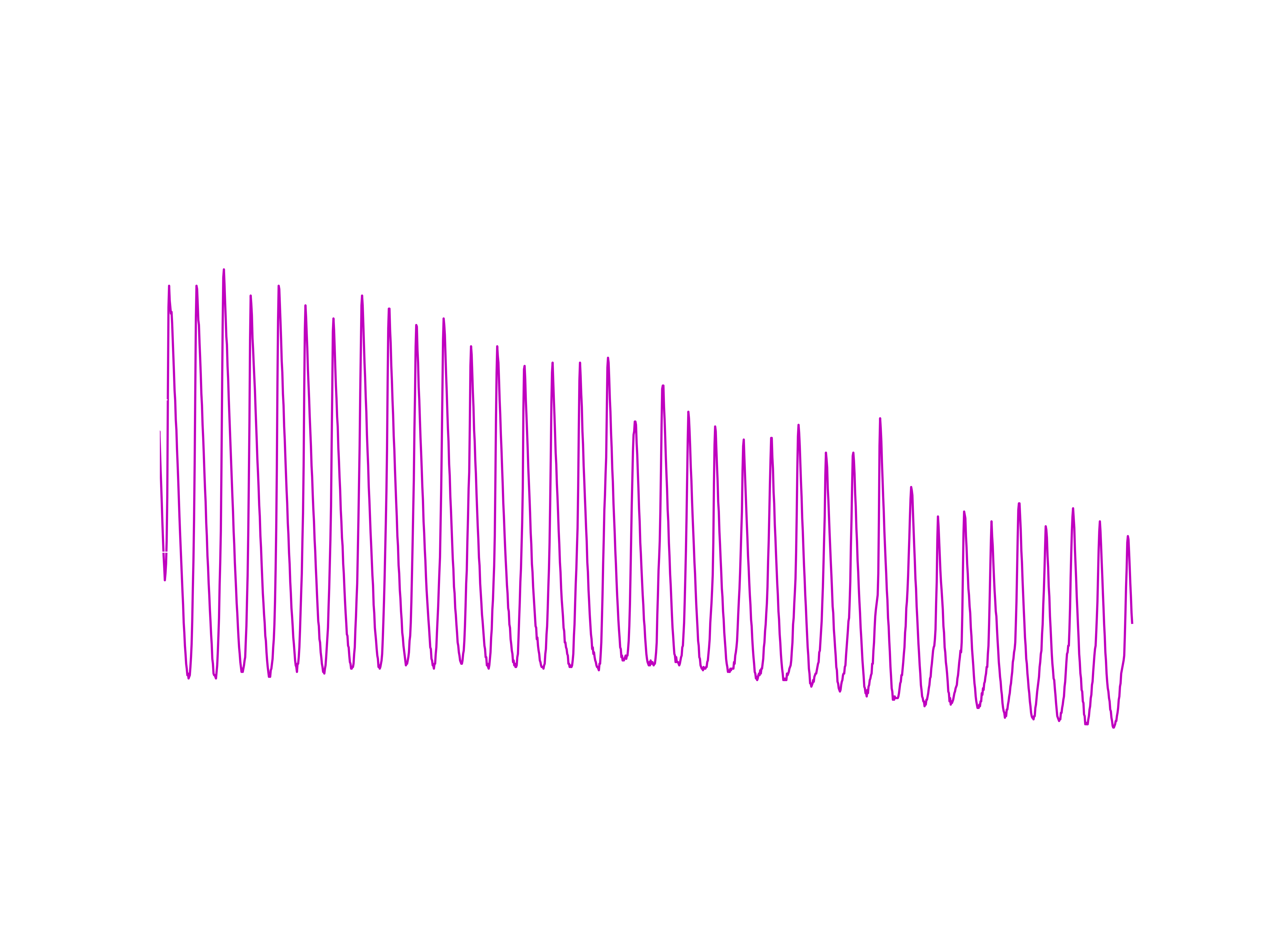
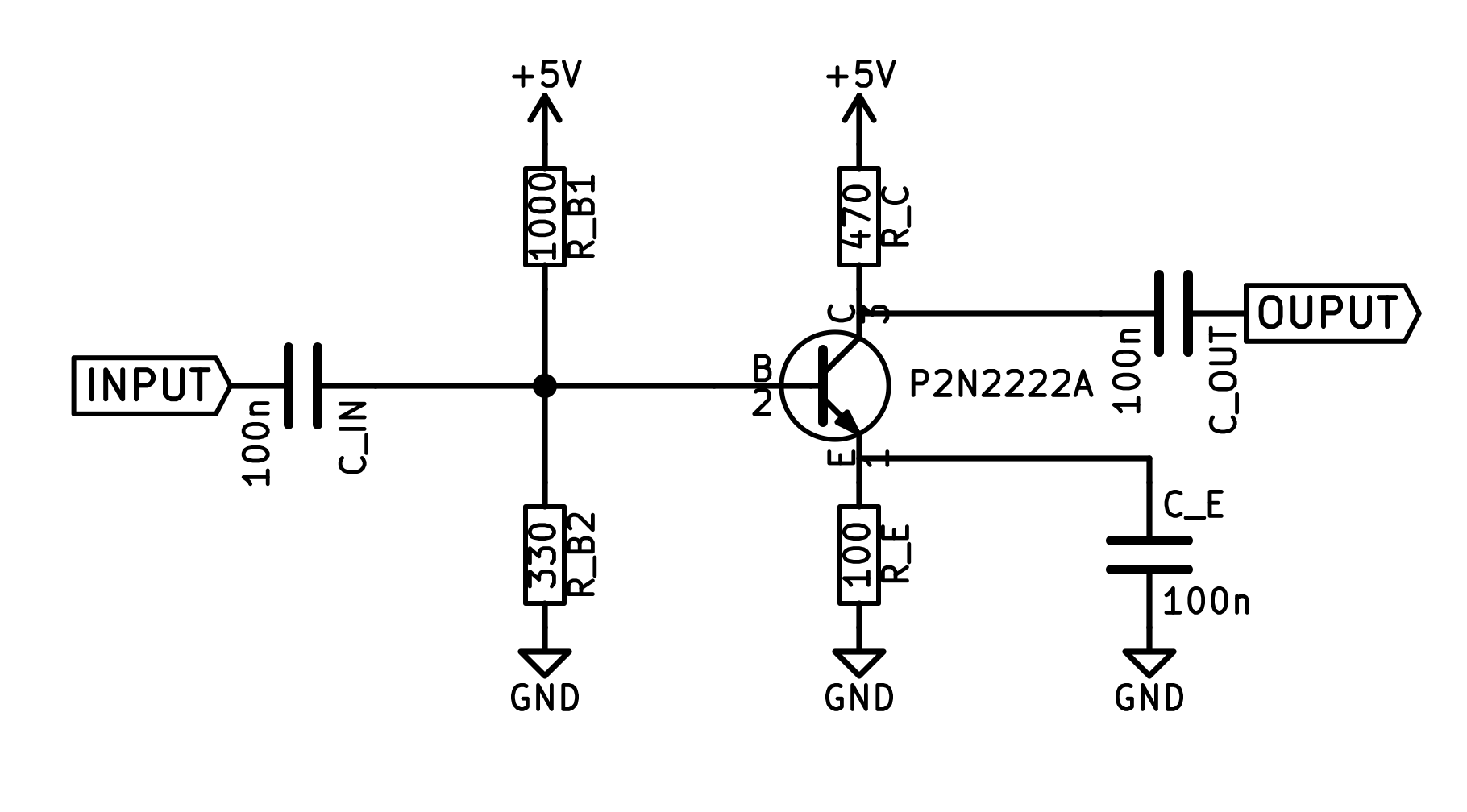 So, here is a time trace of the input to the amp (from the ultrasound transducer) as well as the amp's output. It has gain! In fact, the voltage gain is 47, so the simple calculations turned out to be not too bad. And, the output signal is of about the right amplitude. I am delighted, this amp is just what is needed.
So, here is a time trace of the input to the amp (from the ultrasound transducer) as well as the amp's output. It has gain! In fact, the voltage gain is 47, so the simple calculations turned out to be not too bad. And, the output signal is of about the right amplitude. I am delighted, this amp is just what is needed. 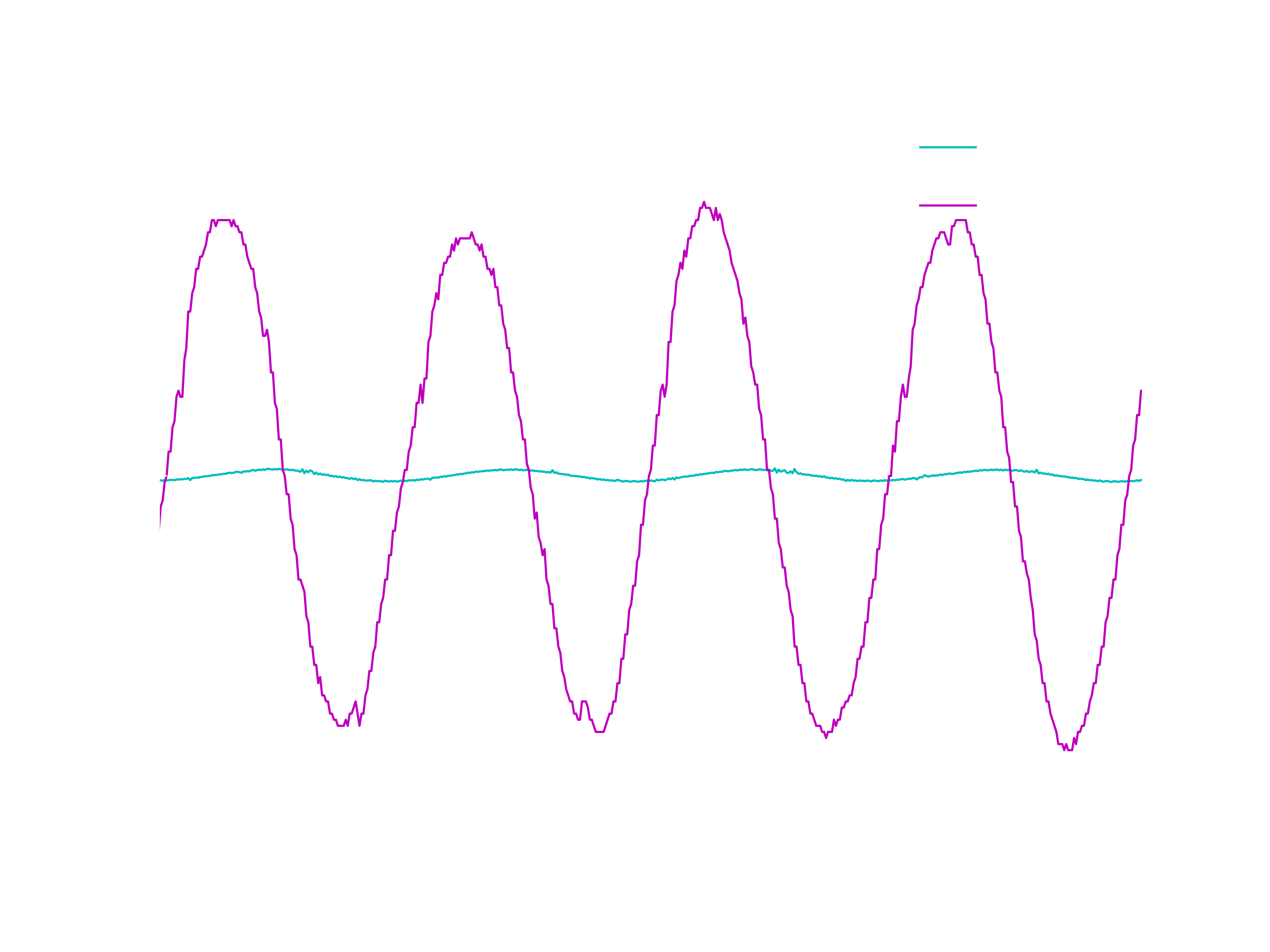
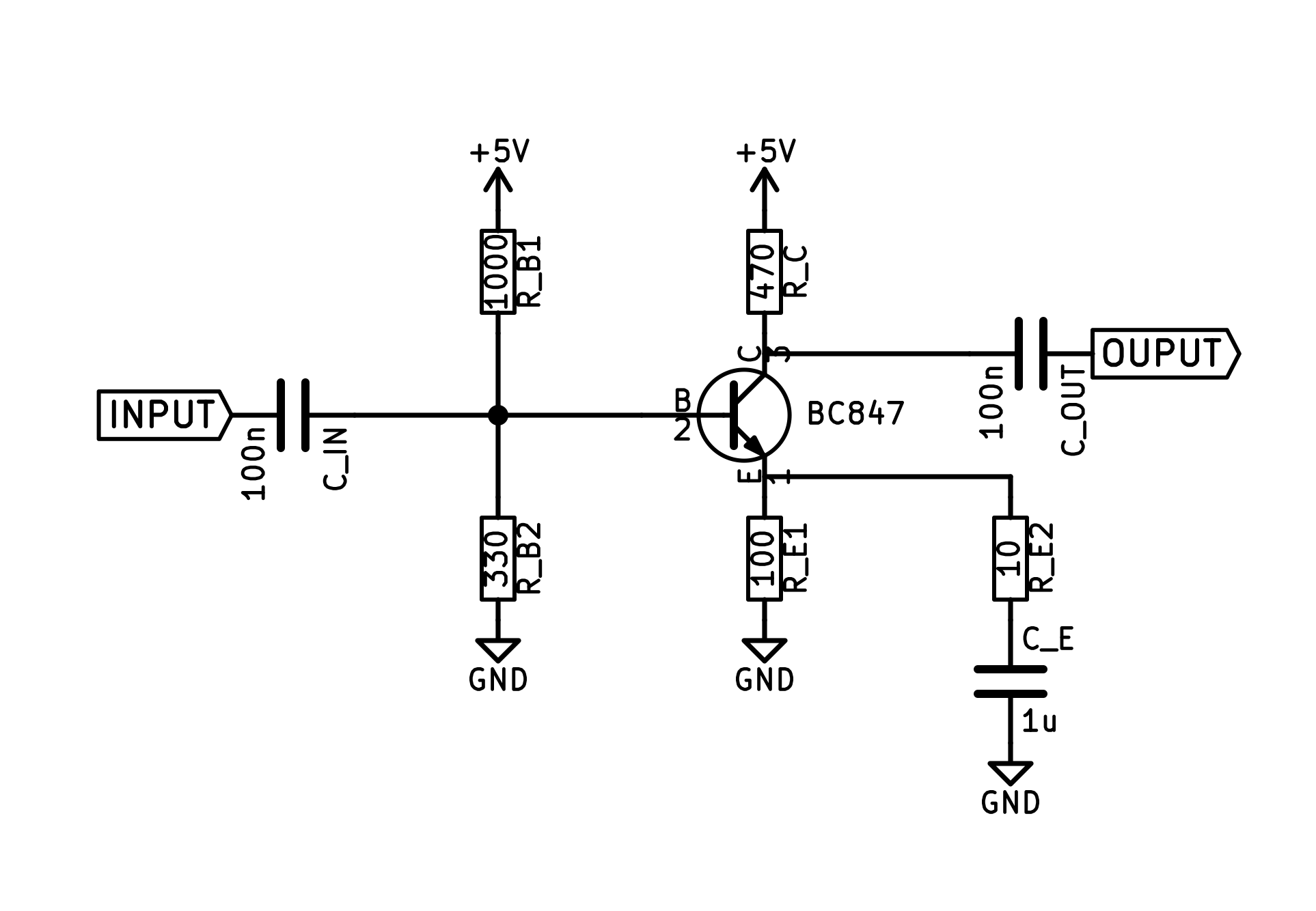
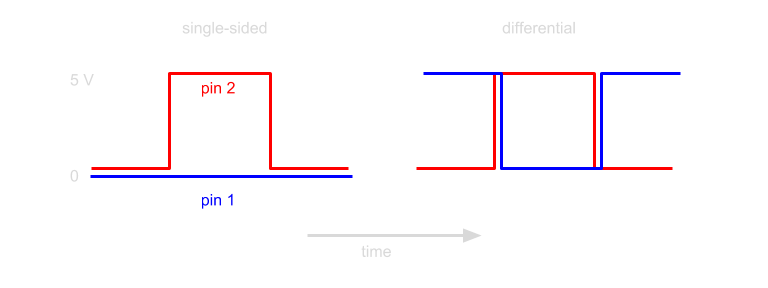
 So this gives me a challenge, to implement a digitally tunable sinusoidal drive in a compact and cheap way. One of the many options would be to use an
So this gives me a challenge, to implement a digitally tunable sinusoidal drive in a compact and cheap way. One of the many options would be to use an 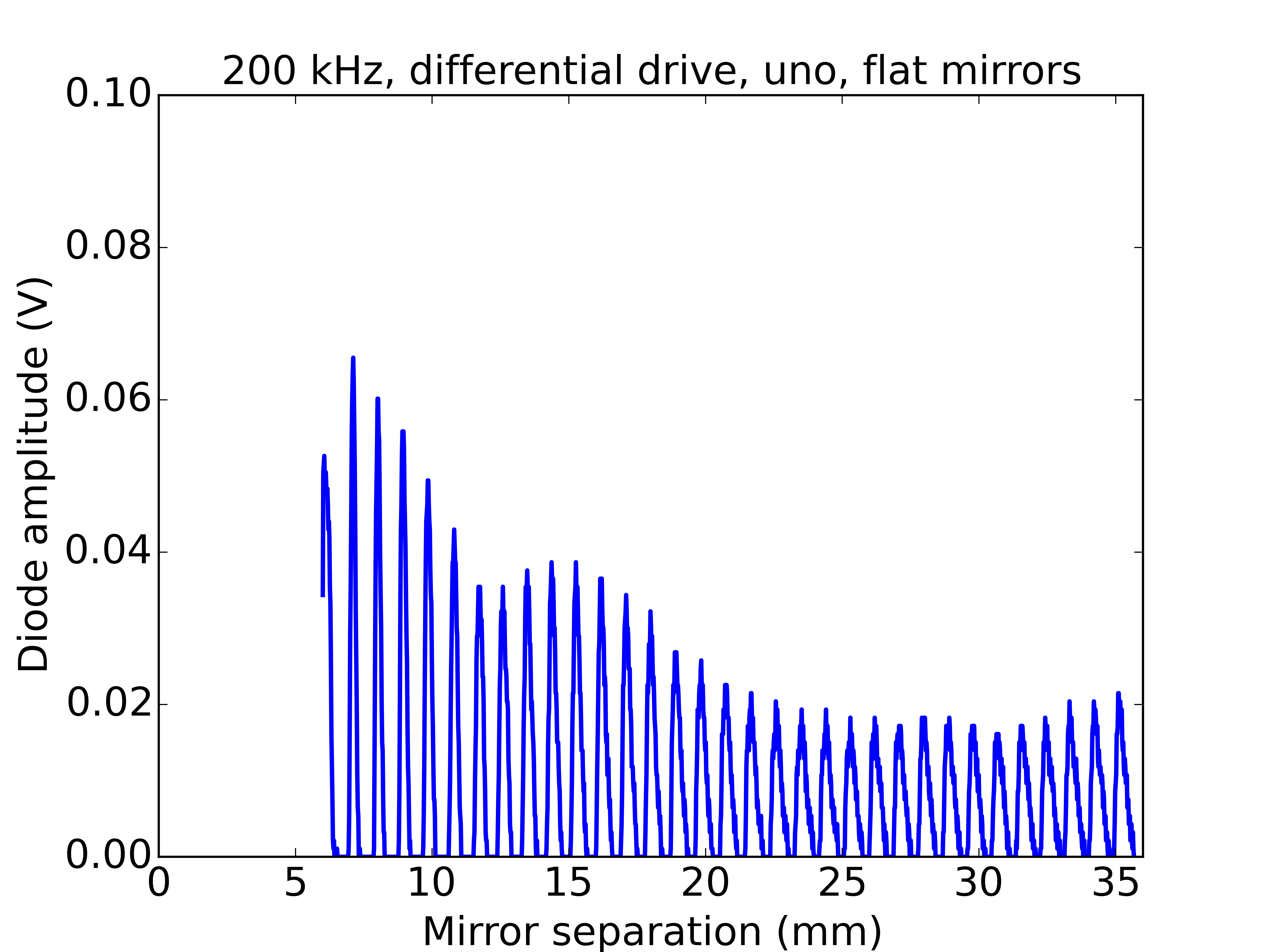








 Scott
Scott
 Petteri Aimonen
Petteri Aimonen
 Marek Materzok
Marek Materzok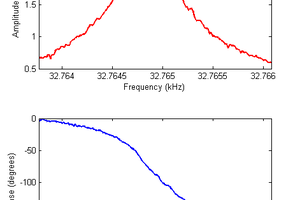
 Dan Berard
Dan Berard
I'm sure you've read through Sam's FAQ pages regarding his DIY Fabry-Perot interferometer. And thank you for describing the concept in terms of the guitar string. I thought I knew how these work, but the analogy helped it gel up in my mind.