French article in GNU/Linux Magazine France
If you wonder why, just click and read the log.
For the what, check Definitions and Draft as well as PEAC vs LFSR for a comparison.
The original algo/project name was "Fibonacci checksum" but it later appeared that it was not the most accurate choice because Leonardo Pisano (the real name of Fibonacci) is the name associated to the periodicity of the sequence under modulo. All I did was add the tiny detail of "end-around carry", or "1-complement addition", which changed everything.
-o-O-0-O-o-
As for how I came to this system...
In 2012, Piano Magic released their album "Life Has Not Finished with Me Yet". One song contains a weird repeating pattern...
Glen Johnson's lyrics are often cryptic and more evocative than objective, but any geek's mind would cling on this mantra at the end:
"Add X to Y and Y to X"
This is really weird but... Why ? What's the point in this obscure "song" with no precise theme or clear subject ? And what does it do ? This last question is the most easily answered : just follow the damned algorithm.
C'est parti...
X=1, Y=0 Y+=X => 0+1=1 X+=Y => 1+1=2 Y+=X => 1+2=3 X+=Y => 2+3=5 Y+=X => 3+5=8 X+=Y => 5+8=13 X+=Y => 8+13=21 Y+=X => 13+21=34 X+=Y => 21+34=55 ...
No need to go further, most of you should have recognised http://oeis.org/A000045, the famous Fibonacci sequence.
This gave me a compelling idea to modify the old Fletcher & Adler algorithms, keeping their very low footprint and minimalistic computational complexity. Both of these well known algos use a pair of values and have a similar structure. The trick is that rearranging the data dependency graph provides the equivalent of a minimalistic polynomial checksum, because the result is fed back on itself, in a more robust way than Fletcher's algo.
At first glance, this new checksum loop's body becomes something like :
Y += ( X + datum[i ] ); X += ( Y + datum[i+1] ); i+=2;
This loop body is totally trivial to unroll. As trivial is the design of the corresponding digital circuit. This early version seemed to contain the whole checksum entropy in the last computed value but now X and Y are part of the signature. And the really important enhancement is the use of the carry!
For superscalar 32 bits CPUs, the following code seems to work well though the missing carry hardware (and/or lack of language support) requires more instructions to emulate:
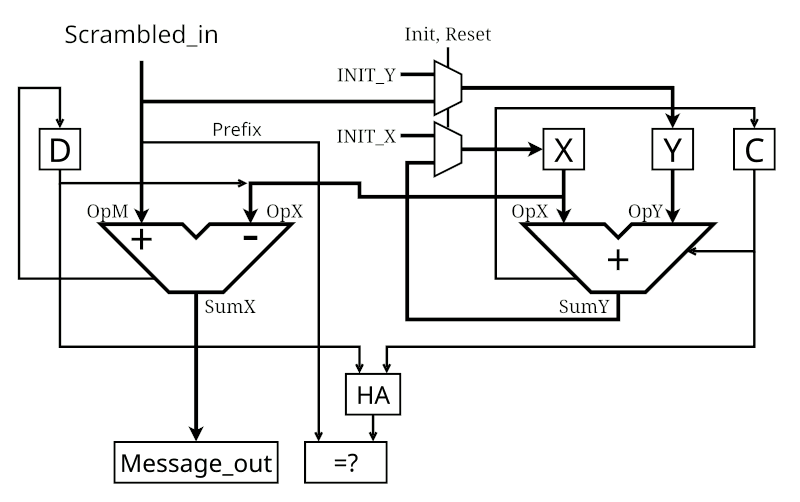
t = X + Y + C; Y = X + data; C = t >> 16; X = t & 0xFFFF;
A more efficient variation exists which does not use a temporary variable:
C += X + Y; Y = X + data; X = C & MASK; C = C >> WIDTH;
In this worst case, without support of a carry flag, that's 5 basic operations (not counting memory loads) that fit in 4 registers and 3 cycles, to process 2 bytes. Not too bad. I'll let you deal with alignment. But is it really safe or safer?
The following logs will show how the idea evolves and the performance increases, through discussions about carry wrap-around, register widths, scheduling, avalanche, parallelism, orbits, structure, and escaping black holes...
-o-O-0-O-o-
Logs:
1. The variable
2. Datapath
3. Adler32 weakness
4. Easy circuit
5. Periodicity
6. A promising 32-bit checksum
7. Progress
8. Why
9. Orbital mechanics
10. Orbits, trajectories and that damned carry bit
11. Two hairy orbits
12. How to deal with black holes
13. Anteriority
14. Moonlighting as a PRNG
15. A new name
16. More orbits !
17. First image
18. Structure and extrapolations
19. Even more orbits !
20. Start and stop
21. Some theory
22. Some more theory
23. Even more theory.
24. A little enhancement
25. sdrawkcab gnioG
26. Further theorising
27. What is it ?
28. A bigger enhancement
29. Going both ways
30. Can you add states ?
31. Please, GCC !
32. _|_||_||_|______|______|____|_|___|_________|||_|__
33. Carry on with GCC
34. A good compromise
35. The new non-masking algorithm
36. Add or XOR ?
37. A 32/64-bit version
38. Closing the trajectories
39....
 Yann Guidon / YGDES
Yann Guidon / YGDES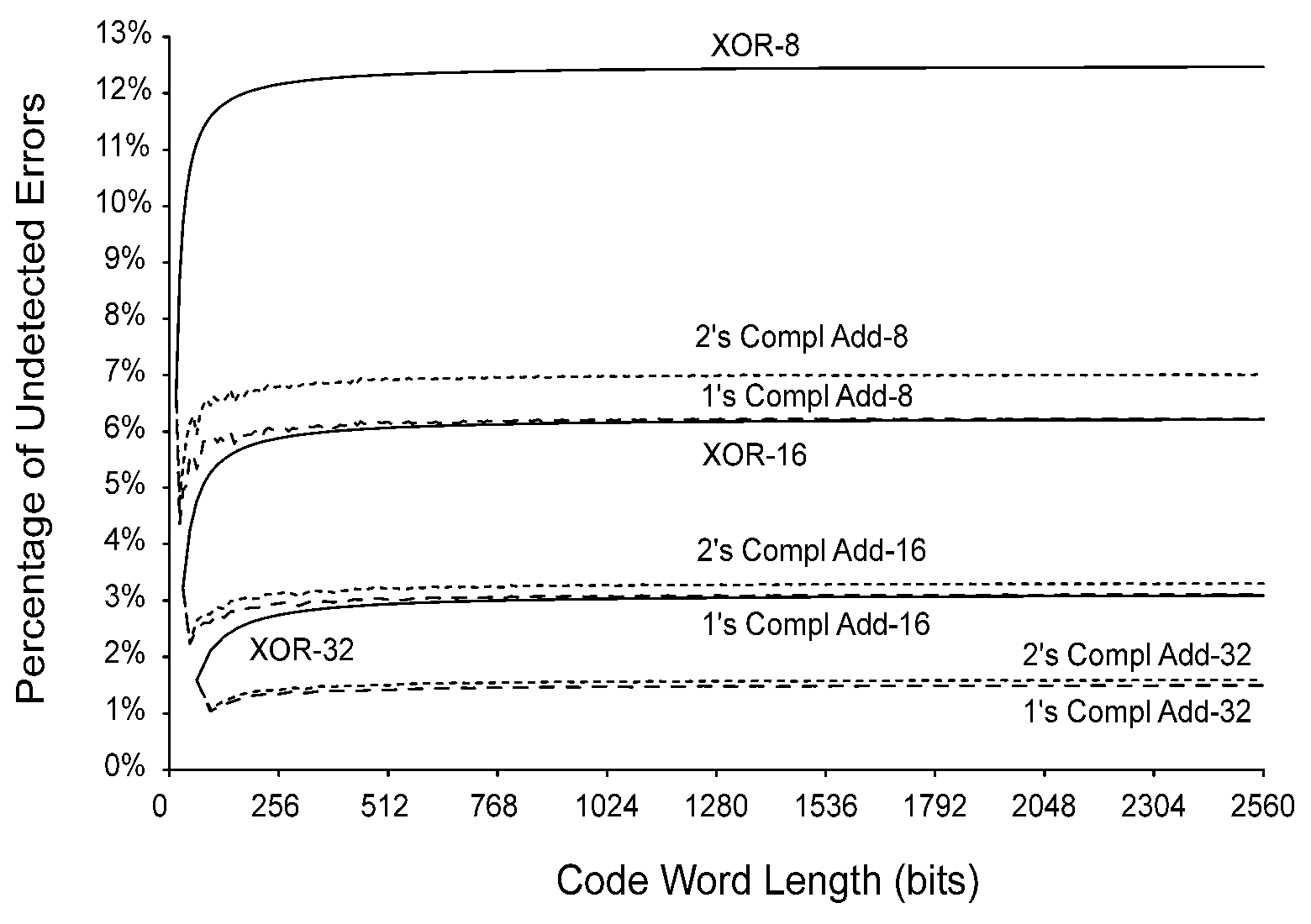





 Tea B
Tea B

https://www.youtube.com/watch?v=EWgts6EiJA0 has some relevant ideas here and there :-)