Bipolar Membrane Energy Harvester

The pH gradient cells and the flow battery cells appear to work, although more data is needed to be certain. Currently we are moving the pH probe between the inside and outside cavity manually, which can cause calibration drift. It would be better if we had two pH probes, calibrated the same initially, so we could directly compare the pH inside and outside of the devices and show that they equilibrate differently at the same time. Using two pH probes would also control for any pH buffer solution that diffuses out of the pH probe tips, potentially causing pH readings to drift. Even without that though, the pH measurements are repeatably higher or lower depending on which direction the ion membrane faces.

There are two additional sources of error to watch out for. First, when the pH probe is rinsed with DI water or removed from the storage solution and placed in the pH gradient cell, it takes up to a few minutes for the probe to equilibrate with the solution. Second, after freshly mixing the liquid, the pH may differ on both sides due to accidental dissolution of gases like CO2 or due to the introduction of contaminants. Great attention must be taken when handling the liquid to ensure no contaminants are introduced.

Also as you will see, if fresh solution is used, it will need to equilibrate with the membrane over the course of hours - using fresh NaOH or NaCO3 solution is not advised once the devices are equilibrated: this could react with the active sites in the ionomer and clog them up if done too many times. For the effect to happen, there must be more unoccupied ionic functional groups on the bipolar membrane than there are ions in solution. If mixing the liquids to extinguish the pH gradient, you should re-mix the liquid already in the cells, and only use DI water to account for evaporation. This will ensure that the liquid is as equilibrated as possible with the device and help avoid contamination as well.

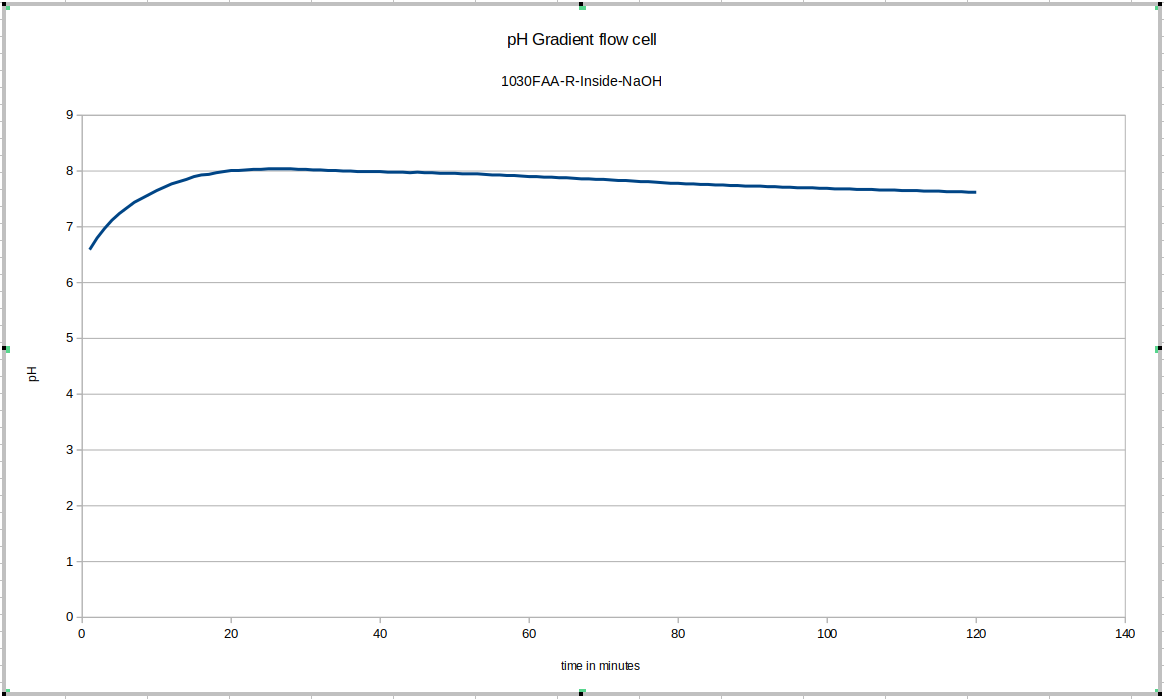
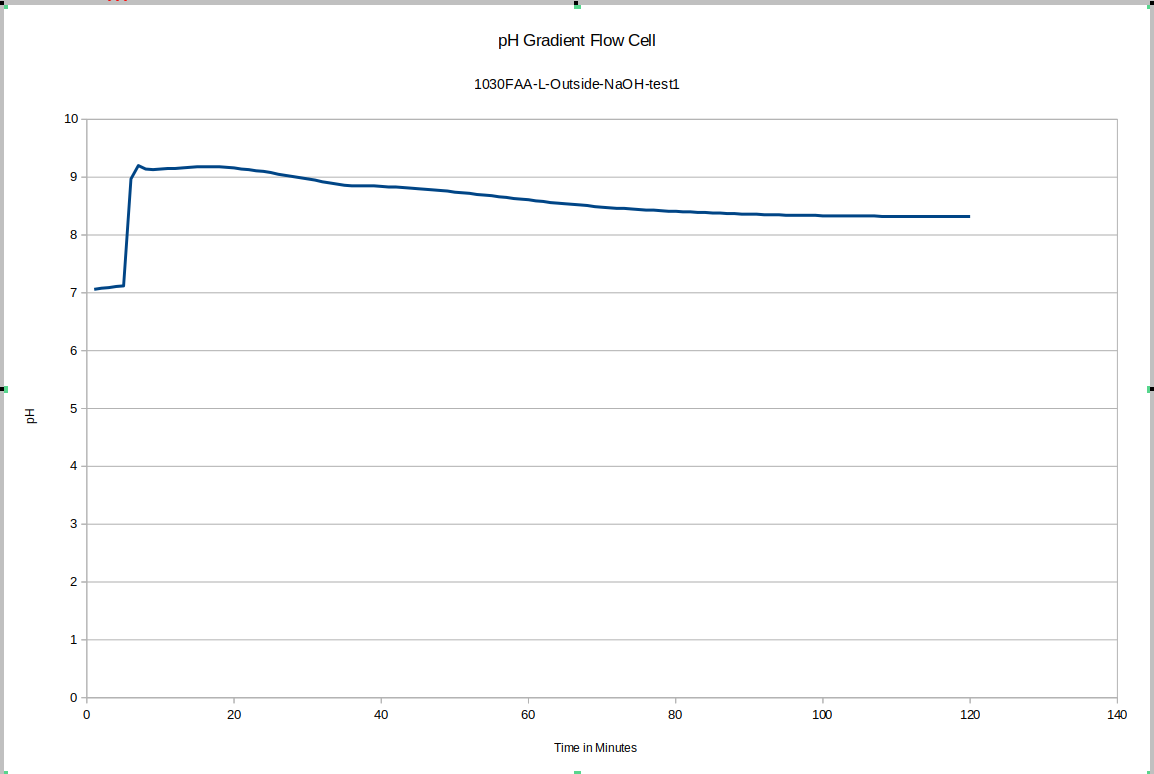
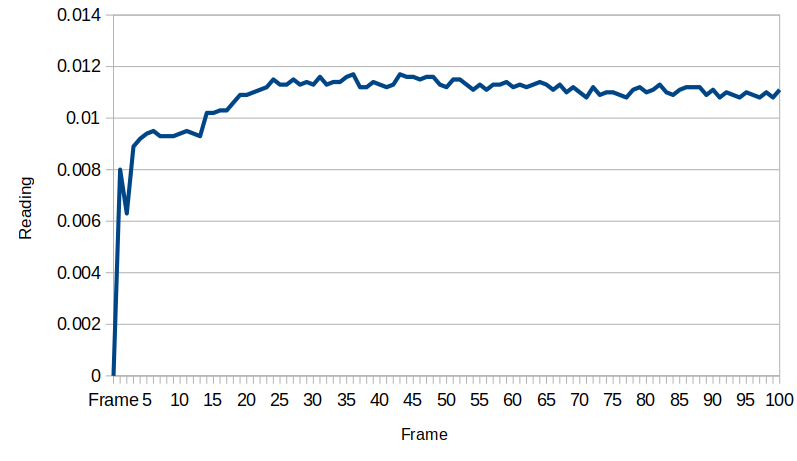
This was the first data acquisition of the pH gradient flow cell. You can see the initial effect of removing the probe from the storage solution and putting it in the test environment, and then you can see that since fresh NaOH solution was used instead of mixing the liquid in the device, longer-term equilibration was still happening. These drifts do not happen in later tests to anywhere close to this degree, once we start accounting for these effects in our experimental procedulre.

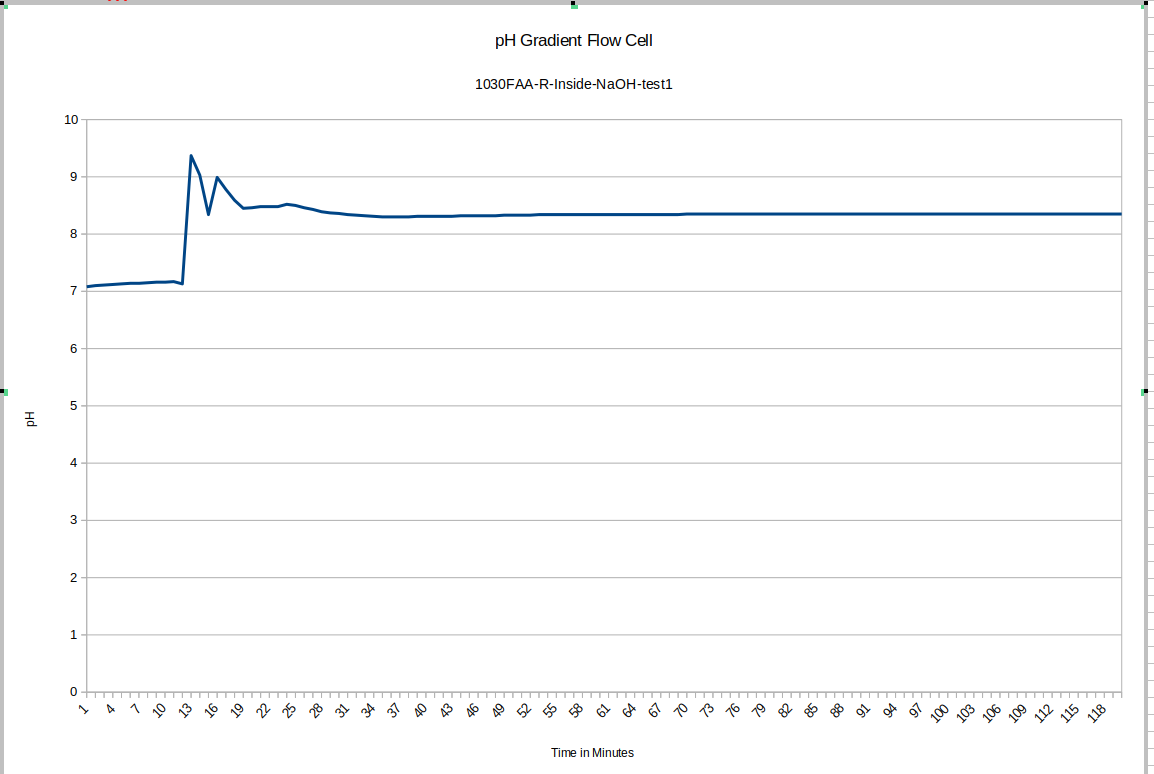
Here again you can see the effect of removing the device from the storage solution and putting it into the test device: this time it is much quicker for some reason: more investigation may be warranted to explain that: it may depend on whether or not the probe was rinsed of storage solution before adding it to the test environment. This test drifts a bunch too: since our maximum pH buffer is 10, it's possible it's not reading properly during the earlier part of the test. This liquid was still equilibrating with the new NaOH solution: we recommend letting everything equilibrate for a few days before beginning testing, and reusing the fluid inside the test device, topping it up with DI water only.

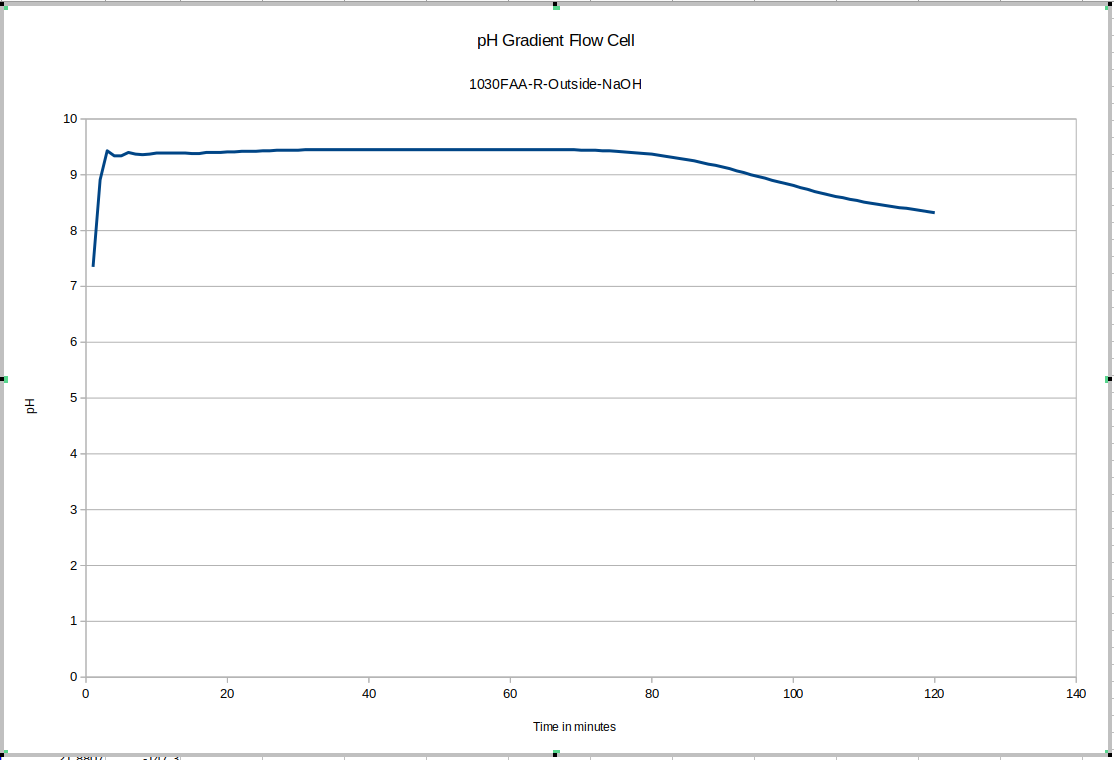
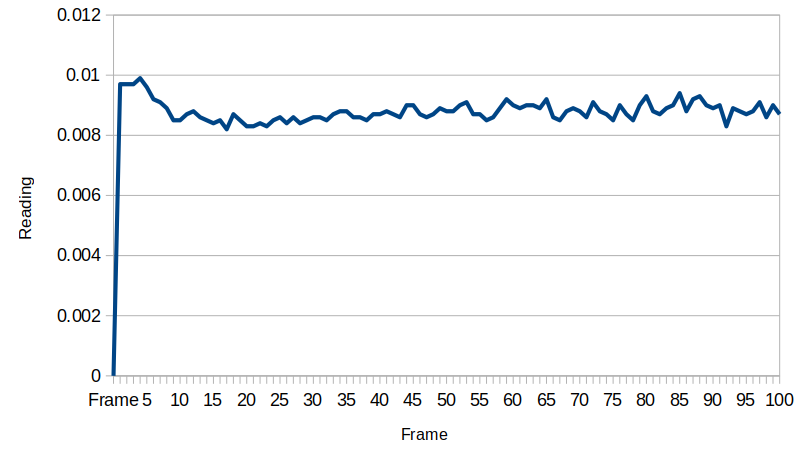
Once we began to account for the sources of error in the first few tests, we started to get data that drifted much less after an initial equilibration period.

For our test device "R" the outside equilibrated to about 7.75 and the inside equilibrated to about 7.58. This is good because as you will see, the test device "L" has its membrane direction reversed relative to "R", and it tends to have the higher pH on the inside.

In this test, the test was started in both cases while the pH probe was in its storage solution. hence the large initial disruption.

Unfortunately, this makes it a little difficult to see, but the inside seems to have a steady-state pH which is about 0.1 higher than the outside, which is the same order of magnitude that we saw in test device "R", which had a pH difference of .17.

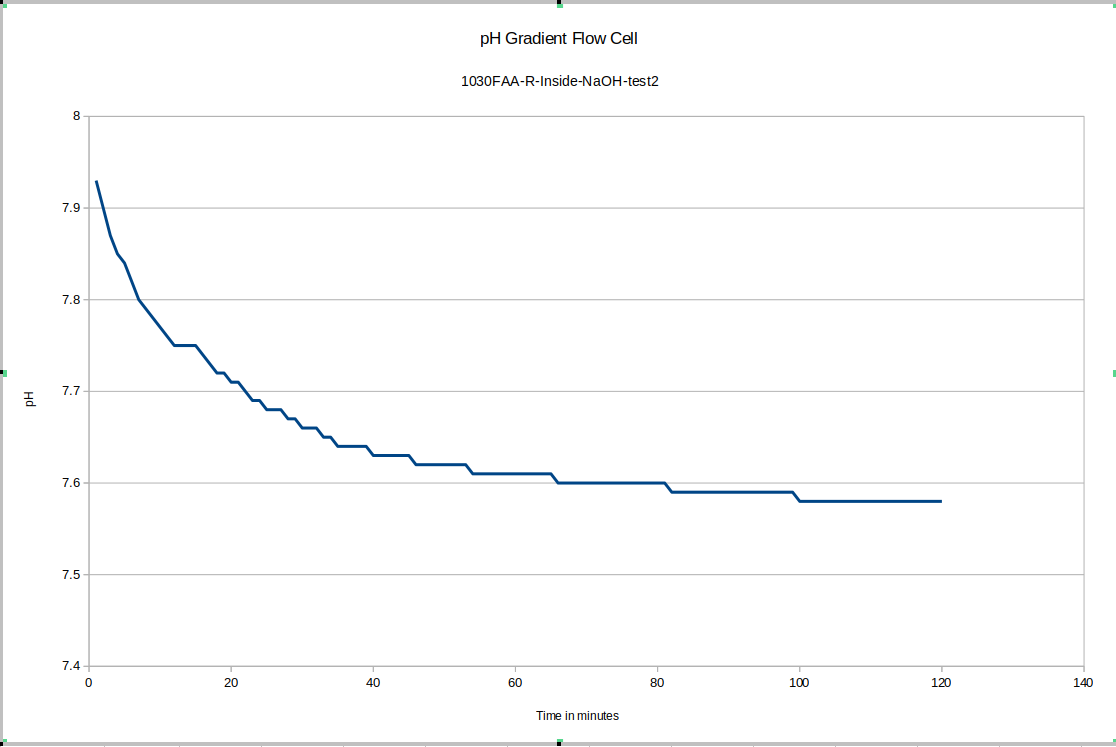
After that test I decided I would try to start the tests after the pH probe was in place in the test environment. I still sometimes caught the tail end of it, but these graphs came out clearer.

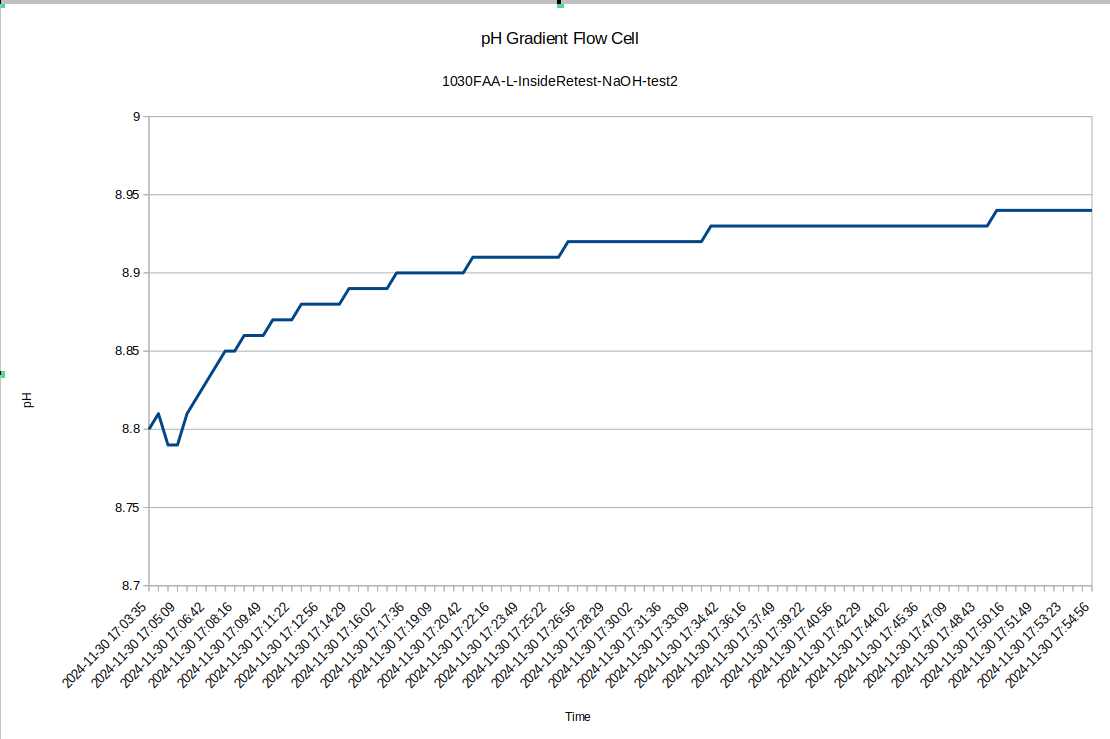
Also for test 2 here I left the device to equilibrate overnight, so the pH difference between the inside and the outside is now very large: about 0.52 with the inside being higher, which is consistent with the previous data.

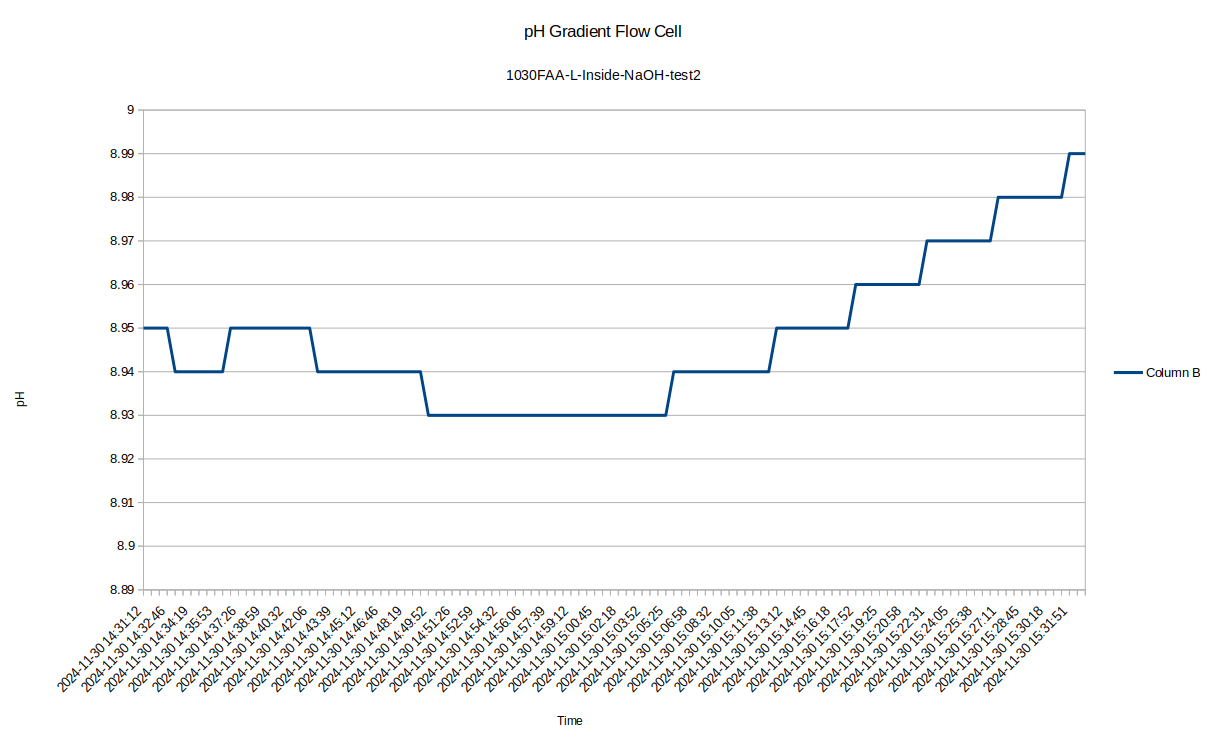
I was surprised to see such a large difference between the inside and outside pH, so I re-tested the inside of the device to see how repeatable the measurements were with the pH probe: I got a measurement of 8.94, so the measurement error seems to be down around .05, which is 10 times less than the pH difference we are seeing!

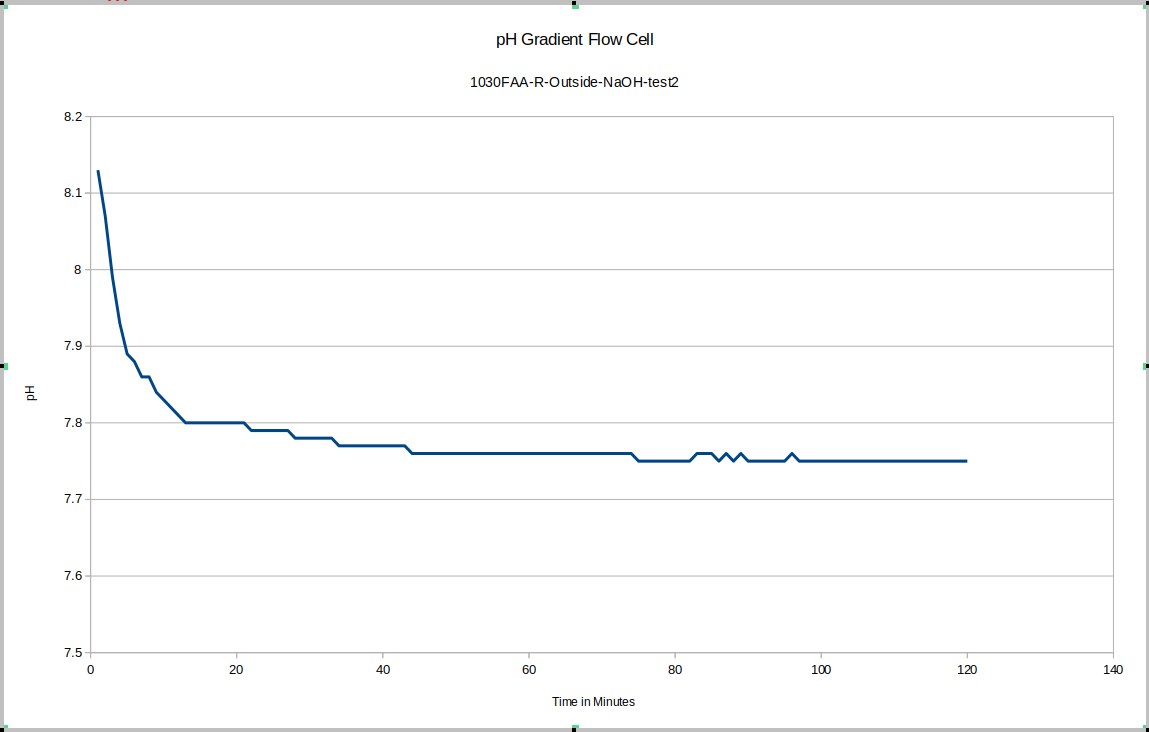
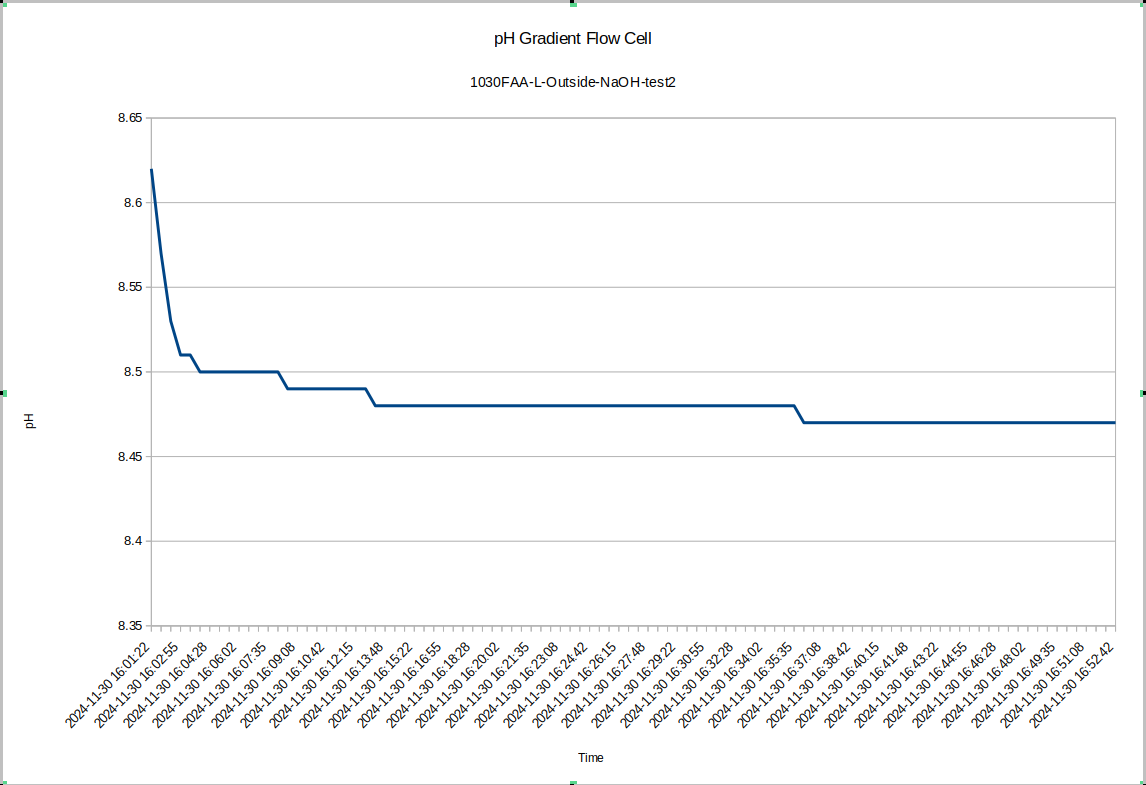
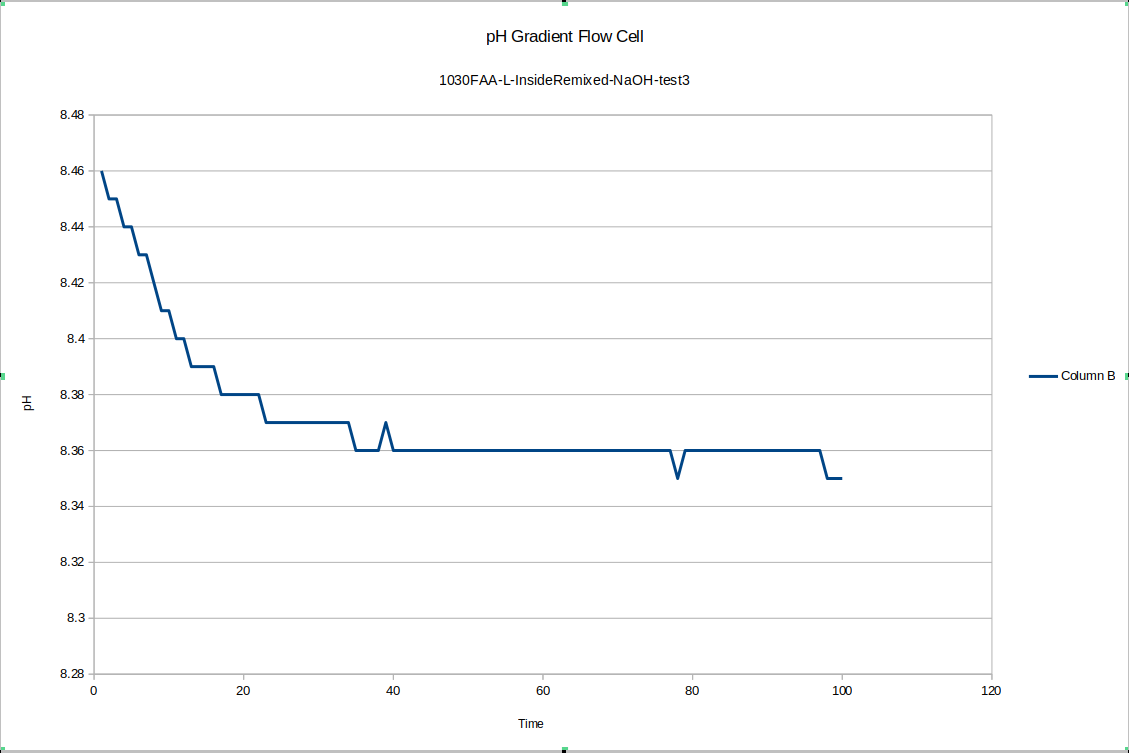
For one final pH gradient test, I remixed the liquid on the inside and outside of device "L" and ran one more test. It seems the slower equilibration may happen after the liquid in the devices is freshly mixed. In any case, a short time after re-mixing the inside quickly stabilized at 8.35

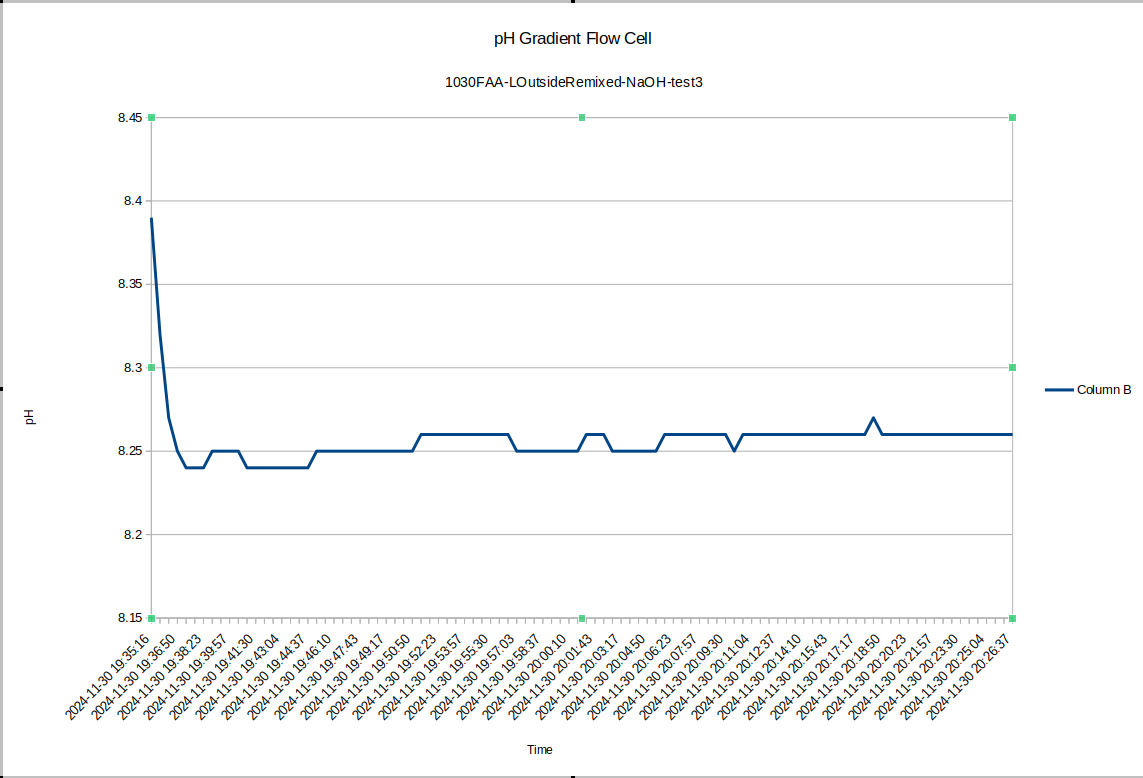
And the outside stabilized at 8.26, with a difference of .09 right after mixing - a little small if the measurement error between those previous tests was .05, but if we let the device equilibrate overnight again, I expect the pH difference will go back up around .5 again. Other similar results exist elsewhere in the literature for pH gradients across bipolar membranes: the bipolar membrane setup on its own does not constitute a nonequilibrium steady state, but one could certainly imagine punching sufficiently small holes in the membrane so that it must do work against the flowback to maintain the pH gradient. So that's tested by our new flow cell design. 

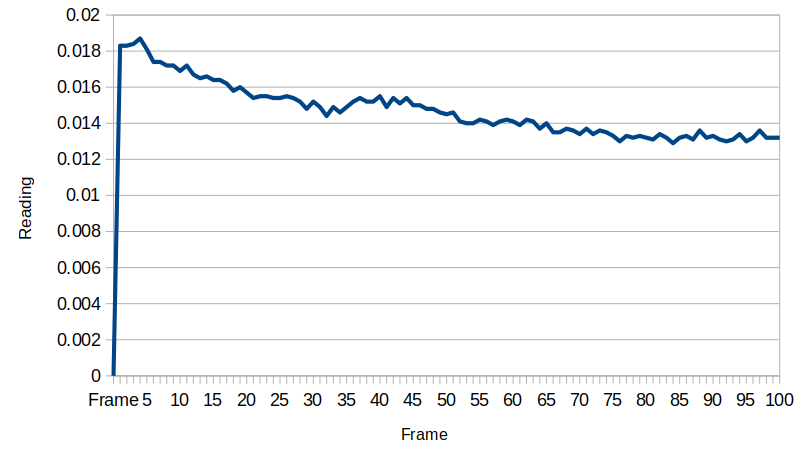
When moved to the test site, a little charge built up which subsequently dissipated: it seems the device gains a little bit of energy from macroscopic turbulence in the water. The voltage stabilizes at about 0.0135 millivolts after a while. The flowback holes provide an electrical resistance that the system works against, and the exponential behavior is related to the capacitance between the two electrodes. We will need to measure that resistance and capacitance to know just how much energy is actually here, but that will introduce energy to the circuit, so we want to take all these measurements first before getting the capacitance and resistance values.

Once the device is shorted, the energy returns, and always in the same direction. Clearly some chemical energy is drained when this happens, as in this case the voltage only went back up to 0.0125 millivolts, but if we wait to the following day, the device always replenishes itself.

After shorting the device again, it holds steady at about 0.09 millivolts. Another thing to note was the temperature in the room cooled down by a few degrees towards the end of the day, and this could also contribute to the voltage reduction. These data are very preliminary and more work is needed to characterize the system behavior better.

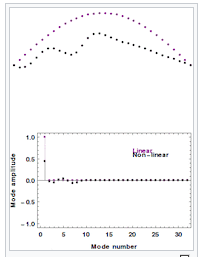
One educated in conservative textbook thermodynamics might be surprised to find that there is a long and venerable history of challenges to the second law of thermodynamics worthy of followup inquiry. The first hint that something was amiss with modern thermodynamics perhaps came in 1953, when Enrico Fermi, John Pasta, Stanislaw Ulam and Mary Tsingou performed discretized simulations of a vibrating string with a nonlinear elasticity (1,2,3,4). This became known as the FPUT experiment or the FPUT problem, after the names of the contributing scientists. In this experiment, it was found that, counter to thermodynamic expectations, when the number of elements in the string was small and when the elements were nonlinearly coupled, the system would not thermalize but rather would undergo periodic recurrence to the initial state (3). It was found that the osscillations could be described as solitons obeying the KDV equation (1), and the symmetries of these solitons enabled the system to avoid ergodicity. 

Here you can see a more modern simulation of the FPUT experiment, courtesy of Wikipedia (1)

For many decades, the FPUT experiment was considered a curiosity, though found to be relevant to experiments involving nanoparticles. It was not a means of extracting energy, but it did show that the assumption of ergodicity might not be valid in all physically realizeable systems.

In the interim, Ilya Prigogine wrote many relevant and well cited papers on nonequilibrium statistical mechanics, but his arguments are sophisticated and I have yet to evaluate the relevance to the present systems of interest in detail - hopefully I can write a followup update later, focused on Prigogine's work once I understand it better. 

Eventually, in 2005 Vladislav Capek and Daniel Sheehan, in their book "Challenges to the Second Law of Thermodynamics", identified some specific statistical mechanical conditions under which deviations from standard thermodynamic behavior were possible (5), providing direction for further experimental investigation. Specifically, they found that statistical mechanical systems with strong quantum mechanical coupling would not necessarily behave in an ergodic manner and that strong coupling can often be found at the surfaces and boundaries of a system. Interestingly, Capek's definition of strong coupling involves non-negligible higher order terms like the second order nonlinearity in the FPUT problem, and due to the discretization of the FPUT problem, it's boundaries are finitely far away, typically a few wavelengths of the principal modes at most just as needed in many of the systems Capek describes, so the findings are in agreement. Moreover, the book mentions that it is well known in biology that receptors couple strongly (by Capek's definition) to the molecules they are meant to interact with via various mechanisms. The importance of behavior at boundaries cannot be understated: strong quantum mechanical coupling becomes very unlikely to happen across large distances, so the two requirements go hand in hand.

In the two decades since the publication of Capek and Sheehan's book, researchers have gleaned further insights into these systems and constructed various devices which demonstrate the concepts involved in practice. The core idea, they realized, was that unusual nonequilibrium steady state systems enabling energy harvesting could be found amongst the set of systems for which the thermodynamic limit is a poor approximation. In practice, this means looking for systems with a small number of particles N, systems where the relevant volume V is small (or equivalently, where the boundaries of the system are nearby), or where the ratio of N to V is variable or tends towards zero or infinity.

Daniel Sheehan subsequently produced an "epicatalytic thermal diode" which when immersed in a single heat bath at above 1200 kelvin spontaneously produced a temperature difference of upwards of 100 Kelvin across a small gap in a thin hydrogen atmosphere with a sufficiently long mean free path, between two appropriately engineered electrodes (6,7,8). And to underscore the physical concept, he followed that up with a room temperature "thermal battery" device (9,10) which is the inspiration for the bipolar membrane devices we demonstrate in the above experiment. Daniel Sheehan continues to explore many other example systems, with the intention of eventually making them physically realizeable (11).

Paul Thibado has noticed energy localization effects similar to the FPUT experiment in graphene monolayers suspended across a gap in a substrate so that it vibrates in response to thermal fluctuations, and has found it possible to harvest thermal motions this way by means of parametric variations in capacitance, using sufficiently fast diodes like MIM diodes, although he tends to speak more conservatively about the implications of these experimental results (12,13,14).

And last but certainly not least, Garrett Moddel has encountered anomalous effects which could be explained by the insights from Capek and Sheehan in MIM diodes next to casimr cavities. In these systems the presence of the Casimr cavity seems to perturb the steady state situation associated with the Seebeck effect, pushing it out of equilibrium to produce a nonequilibrium steady state (15,16,17). It is unclear whether this is truly vacuum energy as Garrett calls it, or simply asymmetric boundary conditions far from the thermodynamic limit which enable energy harvesting, though it seems to me to be the latter.

Many other researchers like Germano D'abramo have proposed other systems which should exhibit energy harvesting accompanied by an apparent decrease in entropy, and are working on physically demonstrating these systems. For those interested in further study, check out The Unlab on Youtube (18) or the literature citing "Challenges to the Second Law of Thermodynamics ; it was a small conference in 2022 attended by big names like Stephen Wolfram. Many of the talks are excellent and the conference demonstrates that quietly, in the background, this subject is of great interest to some of the top scientists in the world.

References:

1. “Fermi–Pasta–Ulam–Tsingou Problem.” In Wikipedia, September 24, 2024. https://en.wikipedia.org/w/index.php?title=Fermi%E2%80%93Pasta%E2%80%93Ulam%E2%80%93Tsingou_problem&oldid=1247548040.
2. Dauxois, Thierry. “Fermi, Pasta, Ulam and a Mysterious Lady.” arXiv, January 10, 2008. https://doi.org/10.48550/arXiv.0801.1590.
3. Fermi, E.; Pasta, J.; Ulam, S. (1955). "Studies of Nonlinear Problems" (PDF). Document LA-1940. Los Alamos National Laboratory.
4. Zabusky, N. J., and M. D. Kruskal. “Interaction of ‘Solitons’ in a Collisionless Plasma and the Recurrence of Initial States.” Physical Review Letters 15, no. 6 (August 9, 1965): 240–43. https://doi.org/10.1103/PhysRevLett.15.240.
5. Čápek, Vladislav, and Daniel P. Sheehan. Challenges to the Second Law of Thermodynamics: Theory and Experiment. Dordrecht: Springer Netherlands, 2005. https://doi.org/10.1007/1-4020-3016-9.
6. Sheehan, D. P. “Nonequilibrium Heterogeneous Catalysis in the Long Mean-Free-Path Regime.” Physical Review E 88, no. 3 (September 18, 2013): 032125. https://doi.org/10.1103/PhysRevE.88.032125.
   
7. Sheehan, D. P., T. A. Zawlacki, and W. H. Helmer. “Apparatus for Testing Gas-Surface Reactions for Epicatalysis.” Review of Scientific Instruments 87, no. 7 (July 5, 2016): 074101. https://doi.org/10.1063/1.4954971.
   
8. Sheehan, D. P., and T. M. Welsh. “Epicatalytic Thermal Diode: Harvesting Ambient Thermal Energy.” Sustainable Energy Technologies and Assessments 31 (February 1, 2019): 355–68. https://doi.org/10.1016/j.seta.2018.11.007.
   
9. Sheehan, Daniel. “Concentration Cell Powered by a Chemically Asymmetric Membrane: Theory.” SSRN Scholarly Paper. Rochester, NY: Social Science Research Network, May 17, 2022. https://doi.org/10.2139/ssrn.4112190.
10. “APS -2023 Annual Meeting of the APS Far West Section - Event - Experimental Results of a Thermal Battery.” In Bulletin of the American Physical Society, Vol. Volume 68, Number 9. American Physical Society. Accessed November 29, 2024. https://meetings.aps.org/Meeting/FWS23/Session/K01.32.
11. Sheehan, Daniel P. “Supradegeneracy and the Second Law of Thermodynamics.” Journal of Non-Equilibrium Thermodynamics 45, no. 2 (April 1, 2020): 121–32. https://doi.org/10.1515/jnet-2019-0051.
12. Ackerman, M. L., P. Kumar, M. Neek-Amal, P. M. Thibado, F. M. Peeters, and Surendra Singh. “Anomalous Dynamical Behavior of Freestanding Graphene Membranes.” Physical Review Letters 117, no. 12 (September 13, 2016): 126801. https://doi.org/10.1103/PhysRevLett.117.126801.
13. Thibado, P. M., P. Kumar, Surendra Singh, M. Ruiz-Garcia, A. Lasanta, and L. L. Bonilla. “Fluctuation-Induced Current from Freestanding Graphene.” Physical Review E 102, no. 4 (October 2, 2020): 042101. https://doi.org/10.1103/PhysRevE.102.042101.
14. Xu, P., M. Neek-Amal, S. D. Barber, J. K. Schoelz, M. L. Ackerman, P. M. Thibado, A. Sadeghi, and F. M. Peeters. “Unusual Ultra-Low-Frequency Fluctuations in Freestanding Graphene.” Nature Communications 5, no. 1 (April 28, 2014): 3720. https://doi.org/10.1038/ncomms4720.
15. Moddel, Garret, Ayendra Weerakkody, David Doroski, and Dylan Bartusiak. “Optical-Cavity-Induced Current.” Symmetry 13, no. 3 (March 2021): 517. https://doi.org/10.3390/sym13030517.
16. Moddel, Garret, Ayendra Weerakkody, David Doroski, and Dylan Bartusiak. “Casimir-Cavity-Induced Conductance Changes.” Physical Review Research 3, no. 2 (April 20, 2021): L022007. https://doi.org/10.1103/PhysRevResearch.3.L022007.
17. “Zero-Point Energy: Capturing Evanescence. | EBSCOhost.” Accessed November 29, 2024. https://openurl.ebsco.com/EPDB%3Agcd%3A7%3A14426119/detailv2?sid=ebsco%3Aplink%3Ascholar&id=ebsco%3Agcd%3A159924233&crl=c&link_origin=scholar.google.com.
18. YouTube. “The UnLAB.” Accessed November 30, 2024. https://www.youtube.com/channel/UCqC5Gi5IjSlo4daxyLDWSZQ

In conjunction with the recent redesign, we decided to look into alternative solutions to use in our fuel cell.  Specifically, we are looking to compare sodium carbonate, sodium chloride, and sodium borate with the currently used urea borate. 

This is because urea borate must be very concentrated to shift the Ph appreciably, and the expected concentration gradient across the membrane is small. Moreover there were questions about the degree of reversibility once the urea adsorbed to an active site on the ionomer: could it stay ionized? If so, the ionomer membranes could become saturated, and this kills the effect because there must be unoccupied active sites to form the nonequilibrium steady state. Moreover there was a remote possibility that the urea could oxidize under ambient conditions and get used up as a fuel, and the borate ions being trivalent seem to get chelated by the ionomers and remain stuck there over time. The hope with sodium carbonate is that although it is a multivalent acid, it is such a weak acid that it tends not to get chelated when in the presence of sodium ions. Perhaps this could add nonlinear behaviors which improve the output of the devices.

As when initially determining the suitability of materials for this device, we needed to confirm the solutions would not interact with any of the materials used. To do this, we soaked the materials in each of the three solutions. The process was similar to that used in testing materials described in parts 2-1 to 2-5 of the instructions. Unlike when first testing the materials, in this instance we only looked for changes in pH.

As shown in the table above, most of the materials did not react significantly to the different solutions. The only material that showed a significant pattern in changing the pH was silicone, which raised the pH slightly. This is not unexpected, as we did not use silicone in the pervious iteration of the fuel cell because it raised the pH in the initial materials testing as well. We chose to retest because we switched to an aquarium grade silicone to see if that would reduce the reaction, which it seems to have done. Additional testing should be done before we introduce silicone into the fuel cell. We expect aquarium-grade silicone will perform better, because it is designed not to leach chemicals into water.

None of the potential solutions show significant reactivity to the main materials used in the fuel cell, with sodium chloride having the smallest change in pH for the materials overall. In a followup experiment it would be good to collect repeat testing data to perform statistical analysis on these data and get an idea of the standard deviation of each result, but for now this gives us a sense of what works and what doesn't.

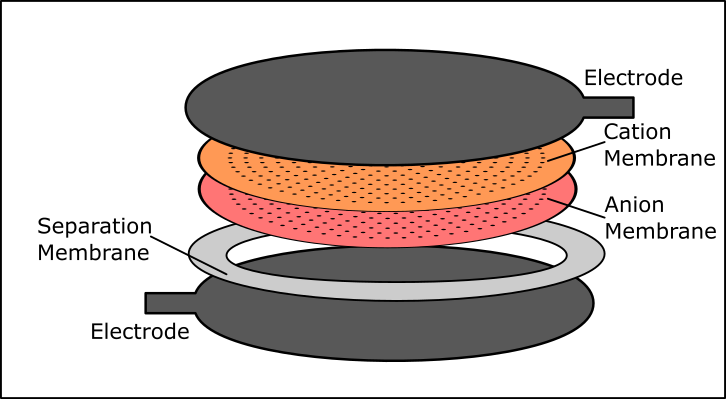
In an attempt to improve the efficiency, repeatability and ease of construction of the fuel cell, we decided to change our approach to the electrode assembly. As we described in the details for this project, two liquids on either side of the membrane are at a nonequilibrium steady state with respect to their boundary conditions. We added a flowback channel, and aim to have a diffusion rate less than that of the bipolar membrane so there is an appreciable pH difference remaining despite the diffusion.

The diffusion path allows recombination of ions and the production of an electric current, but the total path length of the particles must be minimized to make them more likely to take that path: the power of the device drops off exponentially with the path length of the particles, to the square of the distance between the electrodes, and proportionally to the surface area of the electrodes. In the previous setup, we had two small electrodes and one large flowback channel in the center, so that the particle path length may be as large as the radius of the entire device for the particle to make the trip from one electrode to the other, recombine and diffuse back through.

In order to minimize total path length for this otherwise improbable event, we created a series of small holes in the bipolar membrane instead of one large flowback hole. The holes, spaced 4 mm apart with a diameter between .2mm and .05mm depending on the tooling available, will serve as many small flowback channels. Overall this will allow for a larger effective surface area for the electrode as well, because flowback will be evenly spaced over the entire surface of the membrane. We hope this will show a marked improvement over other models, with the smaller path length translating into increased power output. 

We are currently setting up a jig that will allow us to drill holes into the bipolar membrane using a .2 mm micro bit. Using a drill bit should minimize the disruption of the membrane interface over other methods such as piercing the membrane with pins.

In addition to changing the membrane layers in the electrode assembly, there were some changes to the printed flow cell. We closed off the original center opening to the electrode assembly and added two notches opposite one another for the electrode tabs. Additionally we will be making an insertable frame so that the inside of the device can be lined with aquarium-grade silicone or parrafin wax, and an enclosure made of black PETG to keep light away from the device, in case any photocatalytic processes might serve as a source of energy for the device.

Here's our official video for the Hackaday Prize competition:

Another quick update for you! Part 3 of this project (The bipolar membrane flow cell) was completely reworked to make it easier to put together, as well as potentially producing a better pH gradient. Take a look at the updated instructions if you haven't already. We're seeing a pH difference of up to .5 in our latest proof-of-concept devices too. We'll be taking measurements periodically in order to test if this gradient breaks down over time. Keep an eye out for those tables to be posted in the coming weeks.

We recommend studying nonequilibrium statistical mechanics to really thoroughly understand the experiments you can perform with the bipolar membrane devices. The best course I have found on this topic is by Prof. V. Balakrishnan on Youtube.

Here you can find numerous relevant references and related topics of study, including other systems besides the bipolar membrane device, if you wish to try replicating those results as well. Needless to say, research in this field is still quite active.

1. Bai, C., and A. S. Lavine. “On Hyperbolic Heat Conduction and the Second Law of Thermodynamics.” Journal of Heat Transfer 117, no. 2 (May 1, 1995): 256–63. https://doi.org/10.1115/1.2822514.
2. Bar, Amir. “Linear Response and Onsager Reciprocal Relations,” n.d.
   Barletta, A., and E. Zanchini. “Hyperbolic Heat Conduction and Local Equilibrium: A Second Law Analysis.” International Journal of Heat and Mass Transfer 40, no. 5 (March 1, 1997): 1007–16. https://doi.org/10.1016/0017-9310(96)00211-6.
   
3. Bright, T. J., and Z. M. Zhang. “Common Misperceptions of the Hyperbolic Heat Equation.” Journal of Thermophysics and Heat Transfer 23, no. 3 (2009): 601–7. https://doi.org/10.2514/1.39301.
4. “Brownian Ratchet.” In Wikipedia, September 26, 2022. https://en.wikipedia.org/w/index.php?title=Brownian_ratchet&oldid=1112473938#cite_note-forced-3.  
5. Callen, Herbert B., and Theodore A. Welton. “Irreversibility and Generalized Noise.” Physical Review 83, no. 1 (July 1, 1951): 34–40. https://doi.org/10.1103/PhysRev.83.34.  
6. Čápek, Vladislav, and Daniel P. Sheehan. Challenges to the Second Law of Thermodynamics: Theory and Experiment. Dordrecht: Springer Netherlands, 2005. https://doi.org/10.1007/1-4020-3016-9.  
7. Chemistry LibreTexts. “17.3: Brownian Ratchet,” January 17, 2021. https://chem.libretexts.org/Bookshelves/Biological_Chemistry/Concepts_in_Biophysical_Chemistry_(Tokmakoff)/04%3A_Transport/17%3A_Directed_and_Active_Transport/17.03%3A_Brownian_Ratchet.
8.   D’Abramo, Germano. “On the Exploitability of Thermo-Charged Capacitors.” Physica A: Statistical Mechanics and Its Applications 390, no. 3 (February 1, 2011): 482–91. https://doi.org/10.1016/j.physa.2010.10.031.
9. D’Abramo, Germano. “Thermo-Charged Capacitors and the Second Law of Thermodynamics.” Physics Letters A 374, no. 17 (April 12, 2010): 1801–5. https://doi.org/10.1016/j.physleta.2010.02.056.
10. Danageozian, Arshag, Mark M. Wilde, and Francesco Buscemi. “Thermodynamic Constraints on Quantum Information Gain and Error Correction: A Triple Trade-Off.” PRX Quantum 3, no. 2 (April 26, 2022): 020318. https://doi.org/10.1103/PRXQuantum.3.020318.
11. Démoulin, Damien, Marie-France Carlier, Jérôme Bibette, and Jean Baudry. “Power Transduction of Actin Filaments Ratcheting in Vitro against a Load.” Proceedings of the National Academy of Sciences 111, no. 50 (December 16, 2014): 17845–50. https://doi.org/10.1073/pnas.1414184111.  
12. “Entropic Force.” In Wikipedia, September 7, 2023. https://en.wikipedia.org/w/index.php?title=Entropic_force&oldid=1174355238
13. .  Ethier, S. N., and Jiyeon Lee. “The Flashing Brownian Ratchet and Parrondo’s Paradox.” Royal Society Open Science 5, no. 1 (January 24, 2018): 171685. https://doi.org/10.1098/rsos.171685.  
14. Ghosh, Aritra, Malay Bandyopadhyay, Sushanta Dattagupta, and Shamik Gupta. “Quantum Brownian Motion: A Review.” arXiv, June 5, 2023. https://doi.org/10.48550/arXiv.2306.02665.
15. Higashi, Torahiko L, Georgii Pobegalov, Minzhe Tang, Maxim I Molodtsov, and Frank Uhlmann. “A Brownian Ratchet Model for DNA Loop Extrusion by the Cohesin Complex.” eLife 10 (n.d.): e67530. https://doi.org/10.7554/eLife.67530.  
16. Hoyuelos, Miguel. “Entropy of Continuous Markov Processes in Local Thermal Equilibrium.” Physical Review E 79, no. 5 (May 22, 2009): 051123. https://doi.org/10.1103/PhysRevE.79.051123.  
17. Hwang, Wonmuk, and Martin Karplus. “Structural Basis for Power Stroke vs. Brownian Ratchet Mechanisms of Motor Proteins.” Proceedings of the National Academy of Sciences 116, no. 40 (October 2019): 19777–85. https://doi.org/10.1073/pnas.1818589116
18. .  Iñiguez, José, and Douglas Az. “An Unusually Efficient Coupling of Carnot Engines” 17, no. 2 (2010). Kubo, R. “The Fluctuation-Dissipation Theorem,” n.d. Lee, James Weifu. “Type-B Energetic Processes and Their Associated Scientific Implications.” Journal of Scientific Exploration 36, no. 3 (January 1, 2022). https://doi.org/10.31275/20222517.  
19. ———. “Type-B Energy Process: Asymmetric Function-Gated Isothermal Electricity Production.” Energies 15, no. 19 (January 2022): 7020. https://doi.org/10.3390/en15197020
20. . Levy, George. “Loschmidtʹs Temperature Gradient Paradox – A Quantum Mechanical Resolution,” n.d. Levy, George S. “Loschmidt’s Paradox, Extended to CPT Symmetry, Bypasses Second Law.” Journal of Applied Mathematics and Physics 07, no. 12 (December 20, 2019): 3140. https://doi.org/10.4236/jamp.2019.712221. 
21. Mogilner, Alex, and George Oster. “Force Generation by Actin Polymerization II: The Elastic Ratchet and Tethered Filaments.” Biophysical Journal 84, no. 3 (March 2003): 1591–1605. https://doi.org/10.1016/S0006-3495(03)74969-8
22. . Monroe, Charles W, and John Newman. “An Introduction to the Onsager Reciprocal Relations.” Chemical Engineering Education 41, no. 4 (2007). Nordebo, Sven. “On the Interpretation and Significance of the Fluctuation-Dissipation Theorem in Infrared Spectroscopy.” arXiv, September 18, 2023. https://doi.org/10.48550/arXiv.2309.07837. 
23. Onsager, Lars. “Reciprocal Relations in Irreversible Processes. I.” Physical Review 37, no. 4 (February 15, 1931): 405–26. https://doi.org/10.1103/PhysRev.37.405. 
24. ———. “Reciprocal Relations in Irreversible Processes. I.” Physical Review 37, no. 4 (February 15, 1931): 405–26. https://doi.org/10.1103/PhysRev.37.405. 
25. Oster, George. “Brownian Ratchets: Darwin’s Motors.” Nature 417, no. 6884 (May 2002): 25–25. https://doi.org/10.1038/417025a. 
26. Peskin, C.S., G.M. Odell, and G.F. Oster. “Cellular Motions and Thermal Fluctuations: The Brownian Ratchet.” Biophysical Journal 65, no. 1 (July 1993): 316–24. https://doi.org/10.1016/S0006-3495(93)81035-X. 
27. Physics LibreTexts. “4.1: Introduction to Static and Quasistatic Fields,” May 11, 2020. https://phys.libretexts.org/Bookshelves/Electricity_and_Magnetism/Electromagnetics_and_Applications_(Staelin)/04%3A_Static_and_Quasistatic_Fields/4.01%3A_Introduction. 
28. Physics LibreTexts. “7.4: Fluctuation-Dissipation Theorem,” January 13, 2022. https://phys.libretexts.org/Bookshelves/Quantum_Mechanics/Essential_Graduate_Physics_-_Quantum_Mechanics_(Likharev)/07%3A_Open_Quantum_Systems/7.04%3A_Fluctuation-dissipation_Theorem
29. . Rubin, M. B. “Hyperbolic Heat Conduction and the Second Law.” International Journal of Engineering Science 30, no. 11 (November 1, 1992): 1665–76. https://doi.org/10.1016/0020-7225(92)90134-3. 
30. Sheehan, D. P. “A Self-Charging Concentration Cell: Theory.” Batteries 9, no. 7 (July 2023): 372. https://doi.org/10.3390/batteries9070372. 
31. Sheehan, D. P., D. J. Mallin, J. T. Garamella, and W. F. Sheehan. “Experimental Test of a Thermodynamic Paradox.” Foundations of Physics 44, no. 3 (March 1, 2014): 235–47. https://doi.org/10.1007/s10701-014-9781-5. 
32. Sheehan, D. P., and T. M. Welsh. “Epicatalytic Thermal Diode: Harvesting Ambient Thermal Energy.” Sustainable Energy Technologies and Assessments 31 (February 1, 2019): 355–68. https://doi.org/10.1016/j.seta.2018.11.007. 
33. Sheehan, Daniel. “Concentration Cell Powered by a Chemically Asymmetric Membrane: Theory.” SSRN Scholarly Paper. Rochester, NY, May 17, 2022. https://doi.org/10.2139/ssrn.4112190
34. . ———. “Maxwell Zombies: Mulling and Mauling the Second Law of Thermodynamics.” Journal of Scientific Exploration 34, no. 3 (September 15, 2020): 513–36. https://doi.org/10.31275/20201645. 
35. Sheehan, Daniel P. Epicatalytic thermal diode. United States US9212828B2, filed May 28, 2014, and issued December 15, 2015. https://patents.google.com/patent/US9212828B2/en. 
36. ———. “Maxwell Zombies: Conjuring the Thermodynamic Undead: Modern Descendants of Maxwell’s Celebrated Demon Defy Standard Thinking about Heat Engines and May Offer a Path to a New Kind of Energy Generation.” American Scientist 106, no. 4 (July 1, 2018): 23
37. 4–42. ———. “Supradegeneracy and the Second Law of Thermodynamics.” Journal of Non-Equilibrium Thermodynamics 45, no. 2 (April 1, 2020): 121–32. https://doi.org/10.1515/jnet-2019-0051. 
38. Takuma, Tadasu, and Takatoshi Shindo. “Fundamentals of Electrostatic and Quasi-Electrostatic Fields.” In Problems and Puzzles in Electric Fields, edited by Tadasu Takuma and Takatoshi Shindo, 109–15. Singapore: Springer, 2020. https://doi.org/10.1007/978-981-15-3297-9_5.
39. Gikunda, Millicent N., Ferdinand Harerimana, James M. Mangum, Sumaya Rahman, Joshua P. Thompson, Charles Thomas Harris, Hugh O. H. Churchill, and Paul M. Thibado. “Array of Graphene Variable Capacitors on 100 Mm Silicon Wafers for Vibration-Based Applications.” Membranes 12, no. 5 (May 2022): 533. https://doi.org/10.3390/membranes12050533.
40. Mangum, James M., Ferdinand Harerimana, Millicent N. Gikunda, and Paul M. Thibado. “Mechanisms of Spontaneous Curvature Inversion in Compressed Graphene Ripples for Energy Harvesting Applications via Molecular Dynamics Simulations.” Membranes 11, no. 7 (July 2021): 516. https://doi.org/10.3390/membranes11070516.

We tested the fully assembled bipolar membrane flow cell and posted it to my friend Jeremy's channel. You can see the preliminary results here:

We have a quick update for you, to show an interesting result we had with one of our proof-of-concept devices. 

The bipolar membranes in these devices need to be soaked in a dilute solution of sodium hydroxide because the anion membranes have a quaternary ammonium ion, and they use chloride ions for shipping the membrane. This would make them acidic in our experiments if they are not neutralized.

We ran the experiment without pre-soaking the device and got measurements that were extremely acidic, though there was still a pH difference. There were two devices, one with the anion membrane facing the outer cylinder and one with it facing the inner cylinder. For the device with the anion membrane facing the outer cylinder, the outer measurement was a pH of 2.471 and the inner measurement was 3.264. For the one with the anion membrane facing the inner cylinder, the outer measurement was 3.382 and the inner measurement was 2.475.

All these were much more acidic than the 6.776 pH of the solution used, due to the HCl forming from the chloride in the membrane. We do see a much larger pH gradient than what is expected for this device, which should have fully equalized. We're not sure if the chamber directly exposed to the anion membrane had a lower pH because the membrane was not neutralized, or if the pH gradient we are trying to demonstrate is exaggerated at a lower pH. We plan on exploring this idea at a later date, but wanted to share the interesting results.

Keep an eye out for a much larger update, including a complete overhaul of the bipolar membrane flow cell.