Just about everything has a computer in it these days. Computers are one form of digital logic, but by no means the only kind. Digital logic circuits appear everywhere. Sometimes they are parts of a computer system and sometimes they are completely independent.
Digital circuits or digital logic are primarily concerned with circuits that are in two states: 1 or 0. That 1 or 0 might represent something on or off or a yes/no answer. We might gather lots of those states together to represent numbers or even letters. The key is that the state of the circuit has two discrete states.
Contrast this to analog electronics. An audio signal could have any number of voltage values. An audio amplifier might output 3V and then 3.05V and then 3.1V. Later, it might output 1.2V. All of these are legitimate values. However, it also makes them prone to noise and other effects. For example, if the 3V output gets 0.1V of noise impressed on it, how do we know it isn't the 3.1V signal? We don't. FOr most analog devices, a little noise doesn't hurt much but if you were -- say -- trying to do math by adding two voltages that 0.1V of noise would contribute to getting you the wrong answer.
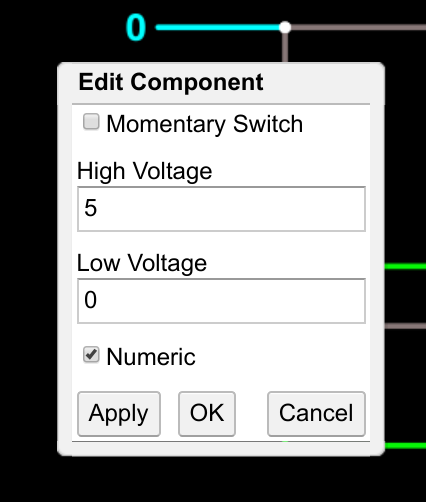
With a digital circuit, there will be some threshold value, usually a voltage. For example, I might decide 0 volts is the 0 state and 5 volts is the 1 state. I could then arbitrarily decide anything under 2.5V is a 0 and anything above 2.5V is a 1. This will offer a lot of noise immunity. Even one volt of noise plus or minus won't affect the circuit at all.
This is the fundamental reason digital electronics are important. Anything that has an on/off characteristic is a natural fit. But by grouping these exact states together we can form very complex logic circuits that will work repeatably like a computer. For example, you can ask your computer to display an exact shade of red because -- for most software -- you can specify 256 values for each color component. Imagine if you had a red light bulb and a knob that made the light brighter or dimmer. That would be an analog device and it might be difficult to get a precise brightness from such a device.
This bootcamp is part of a series:
| Bootcamp 0 | Covers basic digital logic concepts with simulations (this bootcamp) |
| Bootcamp 1 | Introduction to FPGA coding and simulation with combinatorial logic |
| Bootcamp 2 | More FPGA coding and simulation with flip flops (sequential logic) |
| Bootcamp 3 | Working with actual FPGA hardware |
When you are ready, move on to the steps and continue on your FPGA adventure! You'll also find background articles in the project logs. You might want to browse them first and refer back to them as you work through the steps. The logs also have a glossary you can check for any unfamiliar terms.
 Al Williams
Al Williams






 Tim
Tim

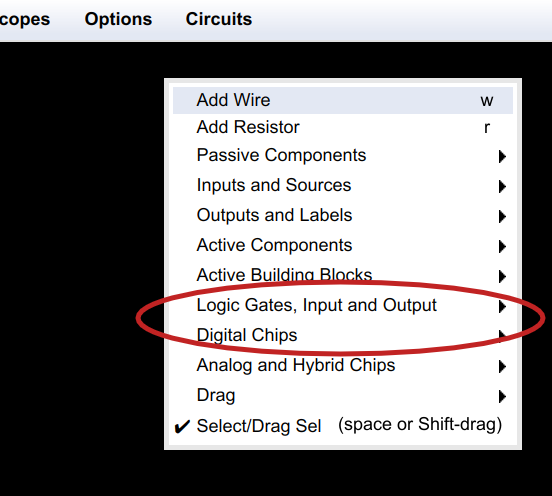
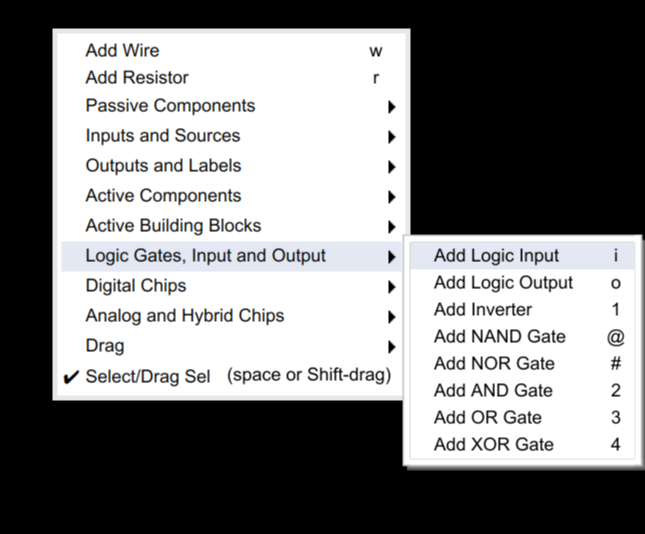
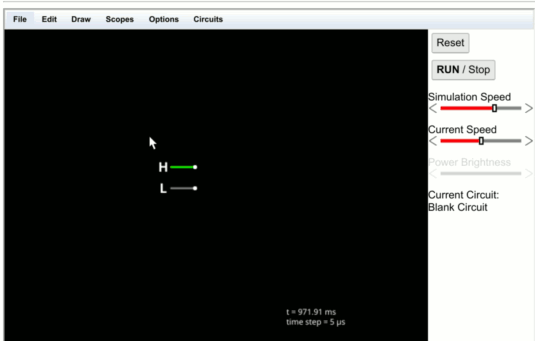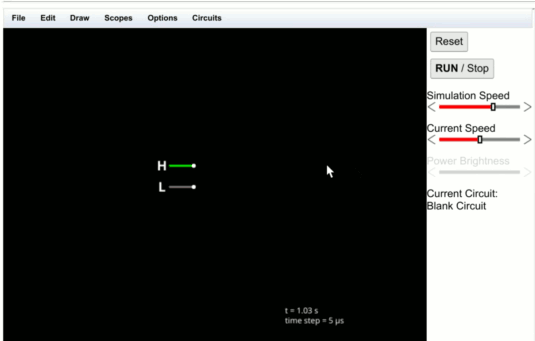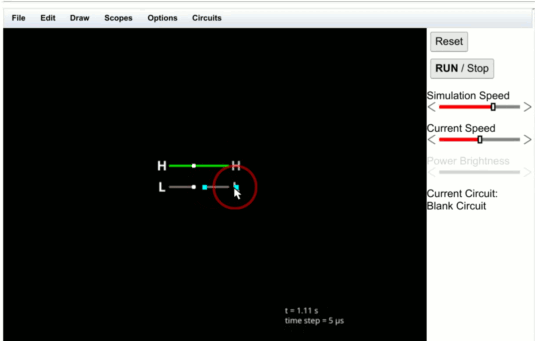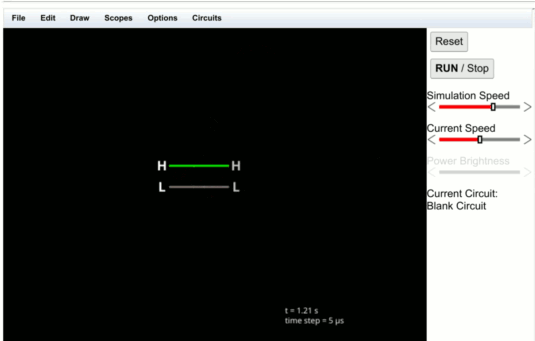
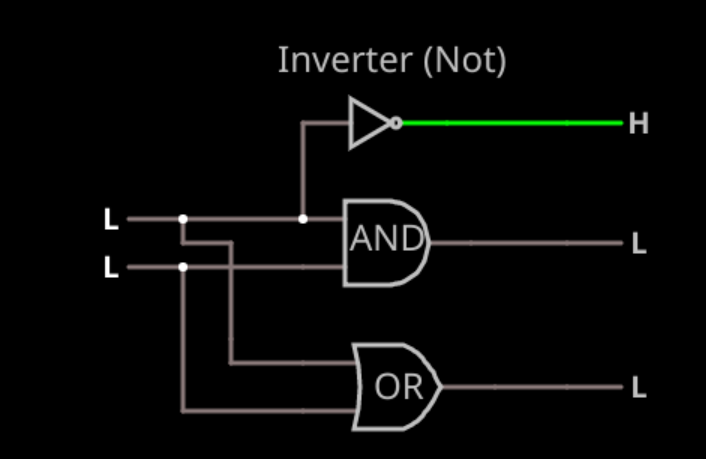
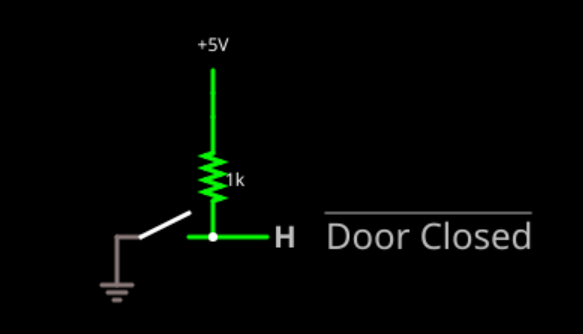
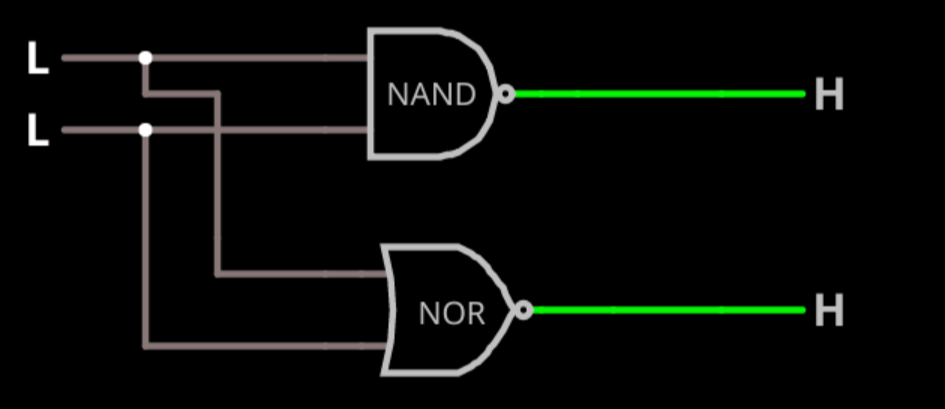
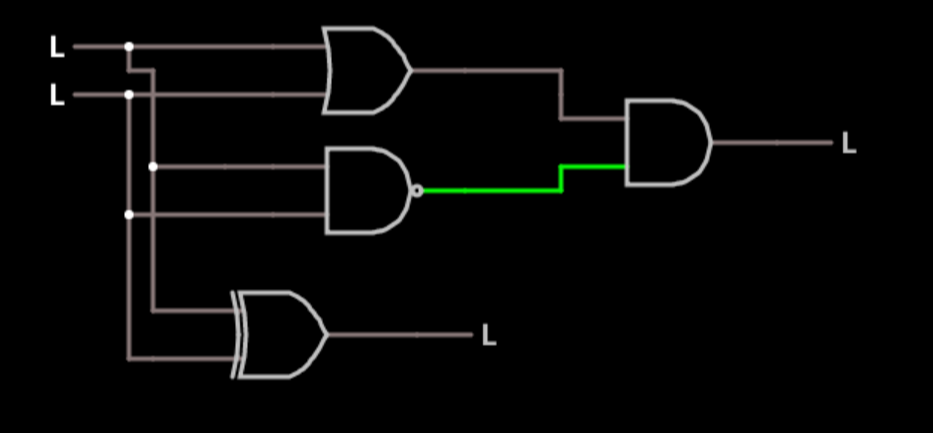
"2 ▇▇▇▇ Understanding Basic Logic Gates ▇▇▇▇ Open the simulator using this link and you'll see ..."
link error
http://tinyurl.com/y9qlmssd%E2%80%8B ---> http://tinyurl.com/y9qlmssd