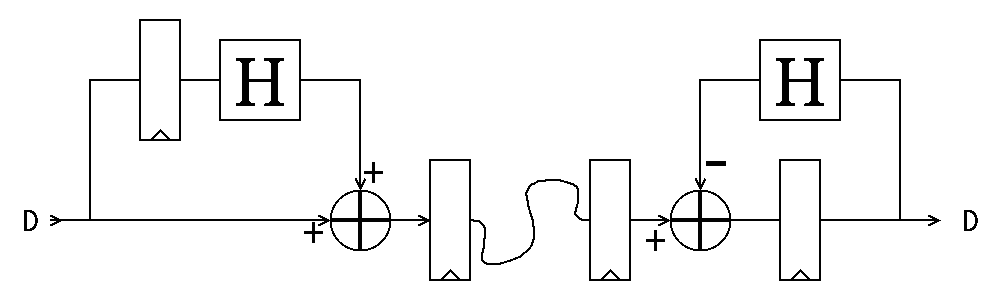-
No more gPEAC ?
01/04/2026 at 11:48 • 0 commentsThe log 181. PEAC w18 is a mixed bag, there are good things but overall, the less good aspects stick.
Given the great performance bump introduced by the Hammer circuit, I wonder why I still keep the gPEAC layer. There are two reasons: it's the best scrambler, and though the very long periods are great, more importantly it can't be "crashed" (which is a flaw of LFSRs).
At a higher level, the system is stronger because it associates two circuits of different nature.
But what if?
.
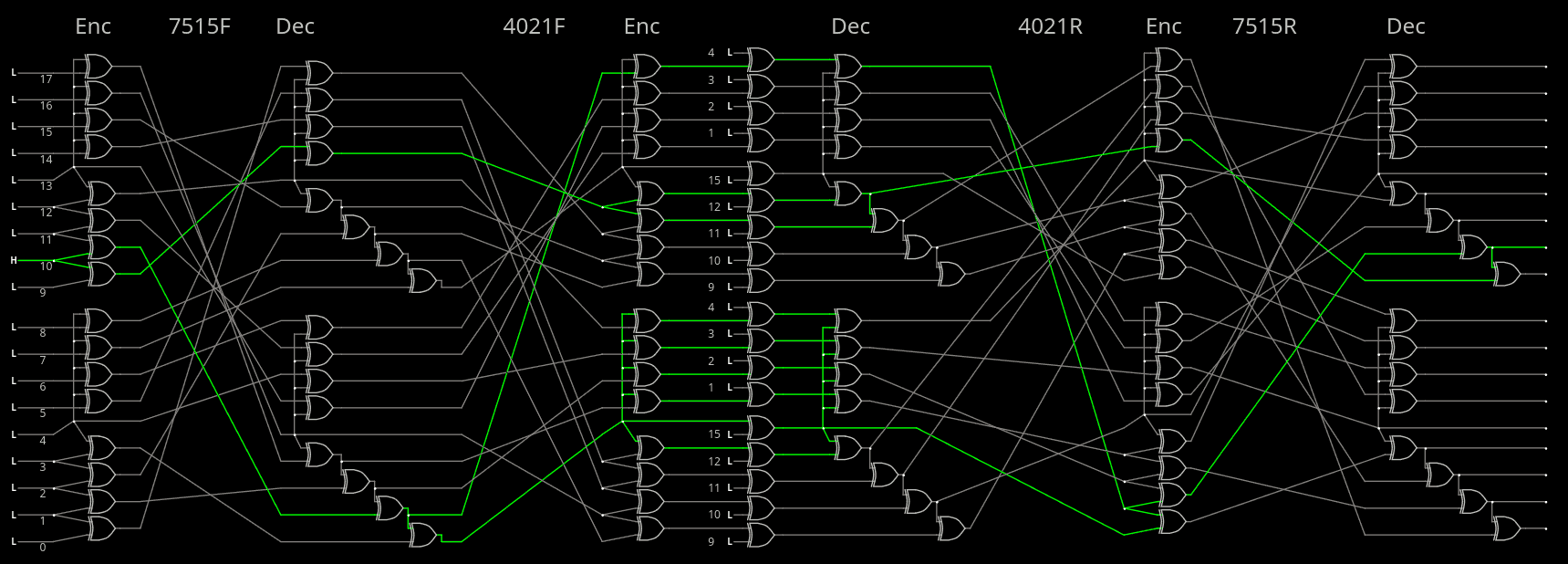
Removing gPEAC removes the scrambler. Is it required ? Even though the miniPHY handles baseline wander (somehow, at least that's the expectation), and even if it uses a sort of convolutional error correction system, the spectrum still needs to be spread. Scrambling also helps a bit to increase error detection.
LFSRs don't work well, they suffer from easy cancellation. Using the Hammer on the send side would be much better (and it's very tempting) but cancellation remains, even though a wider Hammer could provide hidden states. But it wouldn't work. It probably wouldn't improve error detection, which is already maximised.
-
Success
12/29/2025 at 17:03 • 0 commentsThe Hammer18 circuit fits well inside the NRZI unit and instantly delivers fantastic results. Just as expected. That will be my Christmas then!
Here are the results after 10 millions of injected errors:
1 : 2241925 - **************************************************** 2 : 5543183 - ******************************************************************************************************************************** 3 : 1691752 - **************************************** 4 : 369784 - ********* 5 : 112181 - *** 6 : 32917 - * 7 : 6360 - * 8 : 1401 - * 9 : 377 - * 10 : 84 - * 11 : 21 - * 12 : 12 - * 13 : 2 - * 14 : 0 - 15 : 0 - 16 : 0 - 17 : 1 - *
The little 1 at the end is an initialisation bug in the program.
Otherwise, the 4x slope is very apparent: the system has achieved true 2-bit-per-word performance!
There is a little "bump" at the start, 1/4 of the errors are caught immediately, but the next cycle catches 1/2! Then every number is divided by 4 as expected.
- CD0:115 : 115 errors were not caught and passed as the first 0-filled word of a control sequence.
- CD1:6443188 : 2/3 of the detected errors triggered the C/D bit and the rest of the word was not 0. That's 56027× the number of data that passed with a 0.
- Err:3556696 : the rest (1/3) was caught as number errors: either the number was out of range or the MSB was 1.
I'm still unable to explain why the CD bit catches 2× more errors than the other methods, though I'm not sure it matters. However, we have a way to extrapolate the error handling capability.
10 millions (almost 24 bits) give 2 errors at 13 words, 3 more words (4^3=2^6=64) will give about one error in 640 millions (close to 1 billion).
Notes:
- the error model that was tested here is just one bit. Results will vary a bit depending on the error model. More bits and at different positions will affect the curve a little, but not radically.
- Adding another 0-word during C/D transitions will get us in the 5 billion ballpark for rejection. This is actually a requirement since the gPEAC has a one-word latency (hence the bump at the 2nd word) and an error could come at the last data word and go unnoticed, so a second 0-word acts as a checksum check.
- Since the NRZI+Hamming circuit does a LOT of crazy avalanche, now comes the time to check if a more basic binary 18-bit PEAC could work too. I'm looking back at old logs, to find some already-calculated data, and there is
- 19. Even more orbits ! : primary orbit of 18 : 172.662.654 (instead of 34.359.738.368 to pass, or 0.5%)
- 44. Test jobs : 18: Total of all reachable arcs: 68719736689
- 90. Post-processing : Width=18 Total= 34359868344 vs 34359869438 (missing 1094)
In fact I now realise that I have very little clue about the topology of w18. I'm taking care of this at 181. PEAC w18.
And I still need to fix this tiny little bug in the program, that leaves one uncaught error. I didn't notice it before because I always got many leftovers but that bug still appears with no NRZ or Hamming avalanche, even after thousands of cycles : my test code must have a problem somewhere.
....
And it's a weird issue with something that does not clear a register somewhere, it's taken care of by double-resetting the circuit, 2 clocks seems to solve it but what and where... ?
But at least I can get clean outputs:
100 errors:
1 : 23 - *********************** 2 : 61 - ************************************************************* 3 : 13 - ************* 4 : 0 - 5 : 3 - ***
1000 errors:
1 : 229 - ******************************** 2 : 582 - ******************************************************************************** 3 : 154 - ********************** 4 : 23 - **** 5 : 8 - ** 6 : 3 - * 7 : 1 - *
10K errors
1 : 2236 - ******************************** 2 : 5625 - ******************************************************************************** 3 : 1635 - ************************ 4 : 351 - ***** 5 : 108 - ** 6 : 31 - * 7 : 11 - * 8 : 3 - *
100K errors:
1 : 22343 - ********************************* 2 : 55555 - ******************************************************************************** 3 : 16765 - ************************* 4 : 3771 - ****** 5 : 1121 - ** 6 : 348 - * 7 : 79 - * 8 : 14 - * 9 : 2 - * 10 : 1 - * 11 : 1 - *
1M errors:
1 : 223252 - ********************************* 2 : 554817 - ******************************************************************************** 3 : 169397 - ************************* 4 : 37354 - ****** 5 : 11003 - ** 6 : 3274 - * 7 : 701 - * 8 : 151 - * 9 : 40 - * 10 : 8 - * 11 : 3 - *
10 millions:
1 : 2231957 - ********************************* 2 : 5546325 - ******************************************************************************** 3 : 1695563 - ************************* 4 : 371915 - ****** 5 : 112766 - ** 6 : 33113 - * 7 : 6437 - * 8 : 1426 - * 9 : 369 - * 10 : 98 - * 11 : 24 - * 12 : 3 - * 13 : 2 - * 14 : 2 - *len:1 CD0:138 CD1:6449726 Err:3550136 Missed:0 Ham:1 NoNRZI:0
The progress 5, 7, 8, 11, 11, 14 has some hicups... Maybe the PRNG is not random enough?
Anyway, it is great to finally get rid of the "long tail"! Look at this amazingly compliant logplot!
![]()
The 10M slope converges to 15, thus 16 words would be good for 100M. High-safety protocols would still work with 16-word buffers but keep the last one in quarantine too.
And here is another logplot that compares the slope versus the number of (consecutive) flipped bits.
![]()
Get it there : miniMAC_2026_20251230.tbz
-
Looping the Hammer
12/29/2025 at 00:29 • 0 commentsI tried to feed the circuit from itself and see if loops appear, and how long they would be. I start with one bit set:
- Start= 0 or 11 => cycle in 1777 cycles
- 1 : 3556 cycles
- 2 leads to 5 or 16 : 5334
- 3 : not part of an orbit, leads to a 10668-loop
- 4 : leads to 1
- 6 or 8 : 10667
- 7 : 2666
- 9 : not part of a cycle, leads to a 889-loop
- 10 leads to 6/8
- 12 : not part of a cycle, leads to 10668-loop
- 13 : leads to 5 or 16 : 5334
- 14 : leads to 5 or 16 : 5334
- 15 : loop in 2667
- 17 : not part of a cycle, leads to a 762-loop
Actually the lengths of the loops do not matter a lot (unless they are ridiculously short) since this would assume a stream of data=0 which can't happen due to gPEAC.
The fact that the values change so drastically is a big improvement over the previous simple NRZ scheme, since this totally locks the error, while the NRZ could have its effect cancelled as soon as the next cycle if two bits are flipped at the same location on consecutive cycles.
Since the expected buffer size (16 or 32 words max) is way shorter than the observed loop length, there is no need to optimise further, as it could only impede (a bit) directed attacks, not improve error detection in common cases.
And I expect a big jump of error detection eficiency: this additional convolutional layer adds one word of latency but is the key to achieve true 2 bits-per word error detection: 15 words will lead to 1 chance in a billion of leaking an error, and 32 words (64 bits) will make it virtually impossible to pass in real life scenarios.
This also means that a 32-word buffer is all that's needed. In high/medium error rates, there is no need to transmit "empty commands" anymore, saving 2 or 4 intermediate checksums, or about 1/16th of bandwidth! So this new unit is very important for efficiency overall, though it couldn't be enough all by itself, its proterties are complementary to those of the gPEAC layer. It's the pair that works together to reach the theoretical limit.
That new unit also over-scrambles the transmitted data stream. This is not the intended function but it does it (somehow) anyway. So the data's properties must be re-evaluated and at least discarded. This implies that the #miniPHY should expect absolutely random data, no special case... This removes one of the (initially supposed) advantages of gPEAC but it's for the overall best.
-
Hammer = Hamming Maximiser
12/28/2025 at 04:52 • 0 commentsSo we have a unit that takes 18 bits and outputs 18 bits, whose values are as dependent from the others as permitted by only 64 XOR gates. Let's call it the H unit, because it tries to maximise the Hamming distance of the input word.
This has been designed already, and I picked the encoder of a previous log:
![]()
As noted before, it has some of the best possible avalanches I could find: 7 7 8 8 8 8 8 9 9 10 11 11 12 14 14 14 14 15 16 is not perfect but as good as it can be, within the constraints of parsimony of the project.
We also know some of its flaws, by reading the avalanches of the reverse transform : a few combinations need only a few bits to flip only one bit, as indicated by the start of the avalanche sequence : 2 2 3 4 4...
So, since the unit would be looped on itself, another permutation is required to amplify this even more, making sure these few weak bits are fed back to the strongest ones.
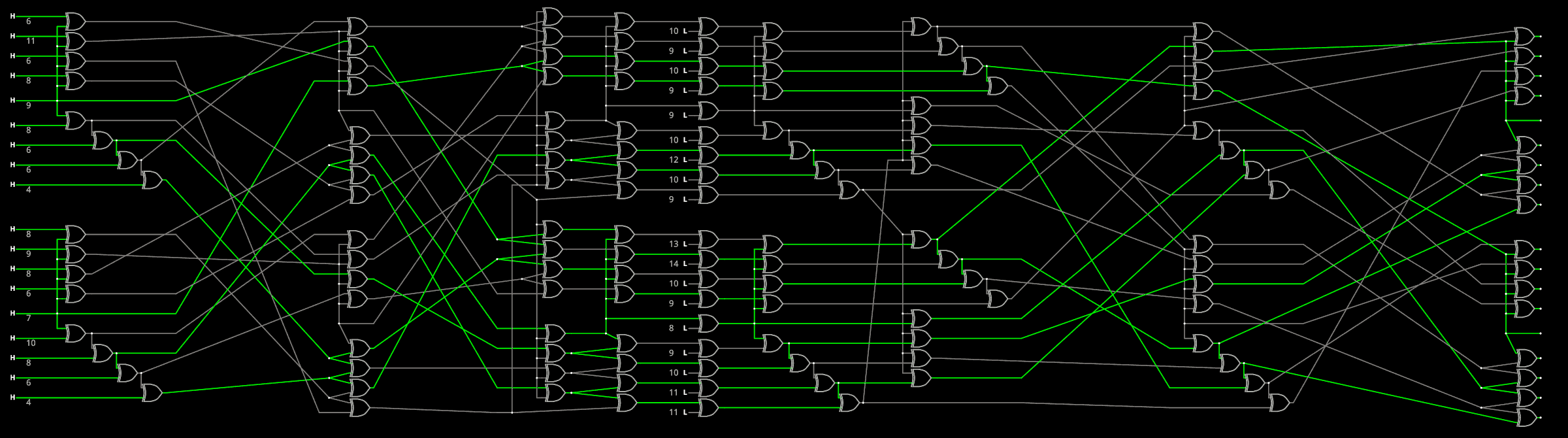
But first, let's untangle this mess because there are a looot of crossings that would make P&R uselessly harder.
...........
The untangled circuit has had a weird episode.
![]()
The score has changed ! 7 8 8 8 8 9 9 9 9 11 12 13 14 15 15 15 15 15
The 16-bit avalanche has disappeared, as well as one of the 7-bits.
However now we have five 15 and the sum of avalanches has climbed to 200 (vs 188 for the original version, max score is 18*18=324). I don't know how or why but that's good !..........Version with even fewer crossings :
![]()
I checked : same behaviours, despite changing the place of the end gates.
....
And now, the VHDL, and...
0 : 13 110111011111011001 1 : 14 110111011111011011 2 : 14 110111101111011011 3 : 13 110111101110011011 4 : 10 010111100100110101 5 : 8 110001101001001010 6 : 8 000000011111111000 7 : 9 101110111001000100 8 : 8 111111000010100000 9 : 15 111111011111111001 10 : 16 111110111111111101 11 : 14 111110111111110001 12 : 11 001101111111010001 13 : 9 000111100010110101 14 : 7 110111000000100010 15 : 9 111111000000101100 16 : 8 100001001111110000 17 : 9 000000011111111010 total:195What the !!!!
7 8 8 8 8 9 9 9 9 10 11 13 13 14 14 14 15 16
5 fewer in total and 16 has appeared again, yet still only one 7,
I give up.
.
After all the minimum requirements are met and too much optimisation toward high numbers make combinations behaving inappropriately.
-
Lemon and lemonade
12/28/2025 at 03:39 • 0 commentsThe last log has shown that the decoder has low performance. The encoder though is quite rad. I could swap them to get the desired result but that would still be insufficient. However it would be good to apply the encoder iteratively to get even better error-spreading.
This means that the Hamming Maximisation circuit is not just in series with 116. NRZ FTW in the pipeline but integrated inside it. In fact the bit-flipping should be inside the feedback loop for greatest efficiency.
![]()
And the beauty here is that the H transform (?) does not need to be a bijection, or provided in reverse form, so the unit is unique, implemented in one instance in the circuit, possibly shared by the send and receive circuits. It could increase in complexity later...
However the study of the reverse transform informs us about some key characteristics. Those are not stellar but the iteration brings the required efficiency. It can still be increased by an output permutation, such that cyclic sequences are not too short.
Another transformation to consider is swapping gates in the maximiser, to reduce wire crossings. I know this will be taken care of by the P&R program but there is no harm in helping it.
-
Proof, pudding.
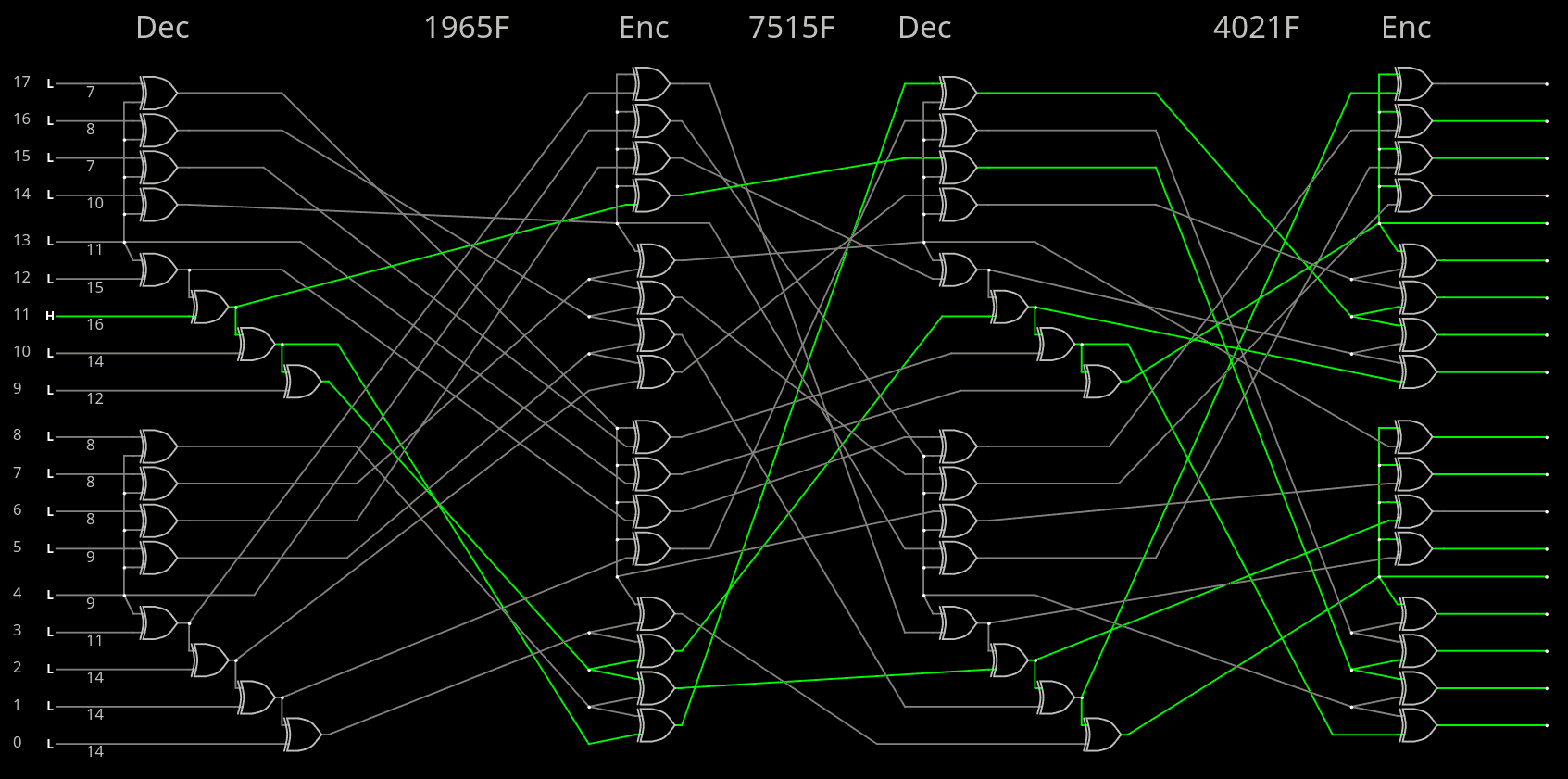
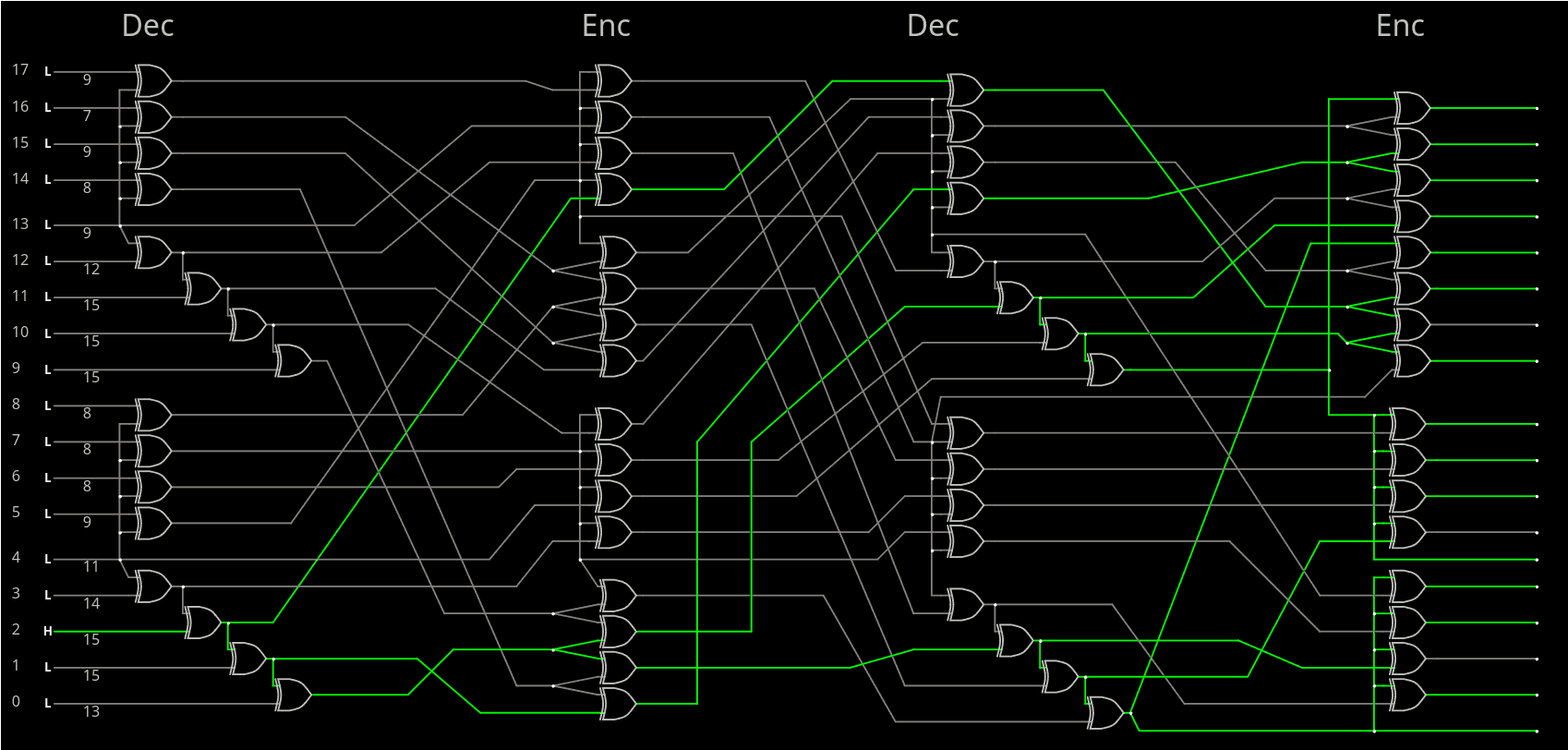
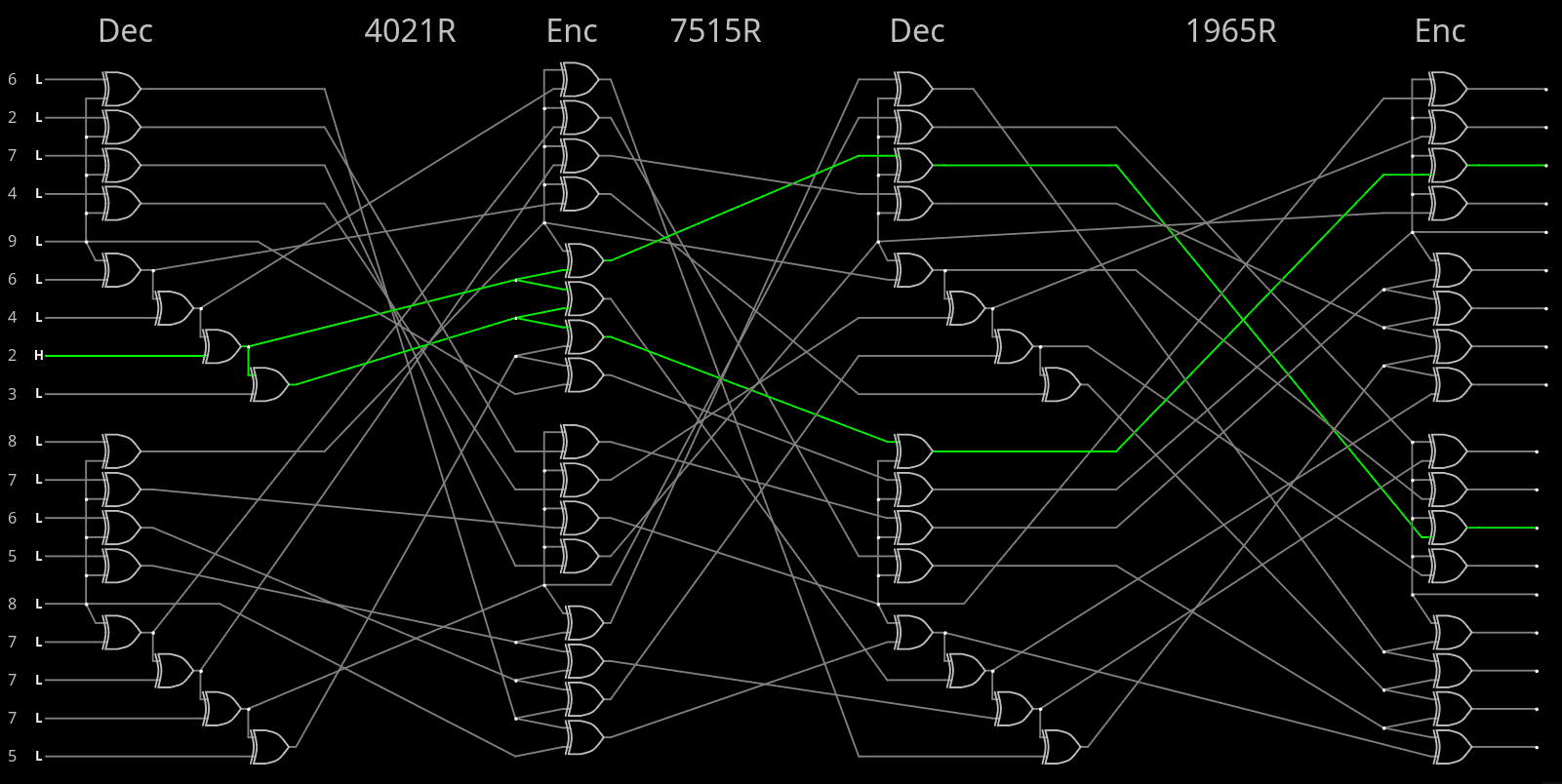
12/27/2025 at 09:04 • 0 commentsAfter some computations, I'm sticking to the balanced configuration with 7-14 avalanche for both decoder and encoder, and I have chosen the first one specified below:
14 188 168 14 7 14 7 - 1965 7515 4021 Perm1965 = forward( 3 5 9 17 16 10 15 12 1 2 0 14 6 7 13 8 11 4 ) reverse( 10 8 9 0 17 1 12 13 15 2 5 16 7 14 11 6 4 3 ) Perm7515 = forward( 17 2 11 0 6 16 8 9 10 14 1 7 13 15 5 12 4 3 ) reverse( 3 10 1 17 16 14 4 11 6 7 8 2 15 12 9 13 5 0 ) Perm4021 = forward( 4 17 6 5 1 15 7 14 16 13 0 9 10 8 12 2 3 11 ) reverse( 10 4 15 16 0 3 2 6 13 11 12 17 14 9 7 5 8 1 )
There are 4 variants but they are just exposing the symmetries of the tiles.
With these sequences of number, it's now time to implement the circuit, starting from the last layer (4021)
![]()
A first obvious feature is that the end of each cascade loops back directly to a quad inverter, so it looks good.
Level 2, the middle permutation layer, implements Perm7515.
![]()
Things start to look great!
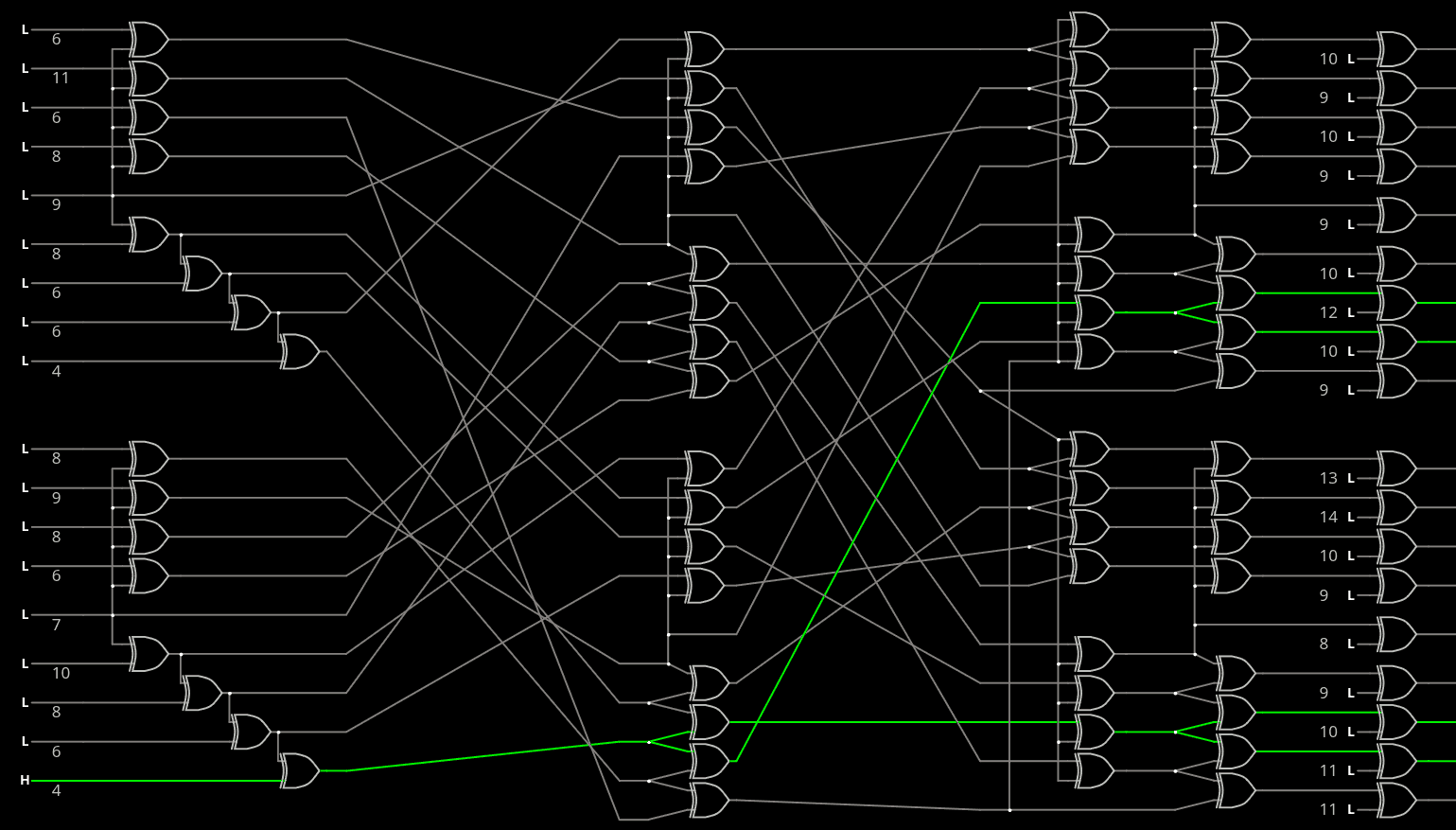
And finally the outer permutation Perm1965. But the circuit has exceeded the size of links so I have split the decoder from the encoder.
![]()
![]()
The manual checks have found that the advertised numbers don't work as expected, and look like the previous two manual version I had created before. So a 5th layer and 4th permutation would be required for a full coverage but... Let's stick to the current config for now, because that's already a lot of gates.
- Encoder: 7 7 8 8 8 8 8 9 9 10 11 11 12 14 14 14 14 15 16 is very good !
- Decoder: 2 2 3 4 4 5 5 6 6 6 7 7 7 7 7 8 8 9 is lousy, worse than 121. MaxHam gen2 !
The discrepancy has no apparent reason for now. But there is a simple workaround: swap the decoder and the encoder, so avalanche is better on the receiving side.
Another "solution" would be to loop the circuits back for another round.
3rd solution : use the highly efficient encoder in the loop of the NRZI converter, to form a combined unit.
-
Brute-forcing in C
12/26/2025 at 07:33 • 0 commentsAs I try to find the best permutations in C, the tiles need to be emulated as well, and I have come up with this C code, optimised for speed on recent OOO CPUs:
static inline unsigned int Encode_layer(unsigned int X) { // inversions unsigned int Y = (X & 0x02010) * 30; // Gray encoding unsigned int G = (X & 0x03C1E) >> 1; return X ^ Y ^ G ; } static inline unsigned int Decode_layer(unsigned int X) { unsigned int Y = X & 0x02010, A = (Y ) >> 4, B = (X & 0x03018) >> 3; Y = Y*30; A ^= (X & 0x0381C) >> 2; B ^= (X & 0x03C1E) >> 1; return X ^ Y ^ A ^ B; }I process both 9-bit "tiles" at once, in the same word (SWAR approach).
For each tile, bits 5-9 are inverted by bit 4, and bits 0-4 are a Gray cascade.
Optimising the permutation was a different story and I opted to allocate 3MB of L3 cache...
..
..
.. (typingtypingtypingtypingtypingtypingtypingtyping)
..
And I was dubious but I got some pretty impressive results. The top ones so far look like this, after the 3rd layer :
min Encoder Decoder sum sum max min sum max min permutation #s 5 99 15 2 165 18 3 1663:1314 5 99 15 2 165 18 3 1672:1476 5 99 15 2 165 18 3 1825:1323 5 99 15 2 165 18 3 1834:1485 5 100 12 2 118 11 3 1087:1380 5 100 12 2 118 11 3 1096:1542 5 100 12 2 118 11 3 1249:1371 5 100 12 2 118 11 3 1258:1533 5 101 14 1 145 14 4 201:1353 5 101 14 1 145 14 4 210:1515 5 101 14 1 145 14 4 39:1362 5 101 14 1 145 14 4 48:1524 5 101 14 1 159 12 4 201:1362 5 101 14 1 159 12 4 210:1524 5 101 14 1 159 12 4 39:1353 5 101 14 1 159 12 4 48:1515 5 102 11 2 120 10 3 476: 108 5 102 11 2 120 10 3 485: 270 5 102 11 2 120 10 3 638: 117 5 102 11 2 120 10 3 647: 279- All of these have a sum of minimum of the avalanche = 5 : either 2 and 3 or 1 and 4
- Both encoder and decoder have a sum of avalanches > 100, sometimes reaching 159...
- The maximum of an individual avalanche is in the 10-14 range
So far I have a good set of criteria to filter further brute-forcing for the 4th layer (3rd permutation). And I have optimised the heck out of it so it produces these results in under 1 second, so the further tests will take only like 20 minutes...
And if I'm patient enough I can relax the thresholds to find more interesting and better behaving configurations.
And it seems that 4 layers could be enough after all :-)
.....................
Adding the 3rd permutation, I get these results:
Min Encoder Decoder Sum Sum Max Min Sum Max Min Perm. numbers 12 127 13 3 200 14 9 1663:1482:1458 12 127 13 3 200 14 9 1672:1320:1467 12 127 13 3 200 14 9 1825:1491:1296 12 127 13 3 200 14 9 1834:1329:1305 12 130 12 3 196 17 9 669:1154: 386 12 130 12 3 196 17 9 678: 992: 395 12 130 12 3 196 17 9 831:1163: 548 12 130 12 3 196 17 9 840:1001: 557 12 99 10 2 203 15 10 218:1241:1478 12 99 10 2 203 15 10 227:1079:1487 12 99 10 2 203 15 10 56:1232:1316 12 99 10 2 203 15 10 65:1070:1325
The decoder gets impressive avalanche but the encoder doesn't take off :-/ the minimum avalanche doesn't get above 3...
Which is explained by a bug in the code ...
.......................
.......................
And with the stupid bug found, here it goes:
13 148 12 5 172 13 8 - 1646:1465:1157 13 148 12 5 172 13 8 - 1655:1303:1166 13 148 12 5 172 13 8 - 1808:1474: 995 13 148 12 5 172 13 8 - 1817:1312:1004 13 148 12 5 184 13 8 - 1646:1465:1166 13 148 12 5 184 13 8 - 1655:1303:1157 13 148 12 5 184 13 8 - 1808:1474:1004 13 148 12 5 184 13 8 - 1817:1312: 995 13 177 13 8 127 10 5 - 1425:1705: 762 13 177 13 8 127 10 5 - 1434:1867: 771 13 177 13 8 127 10 5 - 1587:1696: 924 13 177 13 8 127 10 5 - 1596:1858: 933 13 178 12 8 149 13 5 - 1730: 30:1314 13 178 12 8 149 13 5 - 1739: 192:1323 13 178 12 8 149 13 5 - 1892: 21:1476 13 178 12 8 149 13 5 - 1901: 183:1485 13 195 14 7 150 11 6 - 1731: 854:1016 13 195 14 7 150 11 6 - 1740: 692:1025 13 195 14 7 150 11 6 - 1893: 863:1178 13 195 14 7 150 11 6 - 1902: 701:1187 13 196 15 7 156 11 6 - 398:1847:1353 13 196 15 7 156 11 6 - 407:1685:1362 13 196 15 7 156 11 6 - 560:1838:1515 13 196 15 7 156 11 6 - 569:1676:1524
I expected a slightly higher minimal score, but if a particular behaviour is needed, on the send or the receive side, then we can select a score of 8 at the cost of "only" 5 on the other side.
But these results are actually excellent, in fact. So here is the dump of the four sets of permutations (highlighted above).
Dumping permutations: Perm398 = forward( 6 16 8 3 7 1 17 11 12 15 5 13 0 14 2 4 10 9 ) reverse( 12 5 14 3 15 10 0 4 2 17 16 7 8 11 13 9 1 6 ) Perm1847 = forward( 17 2 9 0 16 6 11 7 8 4 1 12 3 5 15 10 14 13 ) reverse( 3 10 1 12 9 13 5 7 8 2 15 6 11 17 16 14 4 0 ) Perm1353 = forward( 10 1 12 9 5 6 2 7 15 13 4 11 14 0 17 3 16 8 ) reverse( 13 1 6 15 10 4 5 7 17 3 0 11 2 9 12 8 16 14 ) Dumping permutations: Perm407 = forward( 15 7 17 12 16 10 8 2 3 6 14 4 9 5 11 13 1 0 ) reverse( 17 16 7 8 11 13 9 1 6 12 5 14 3 15 10 0 4 2 ) Perm1685 = forward( 4 1 12 3 5 15 10 14 13 17 2 9 0 16 6 11 7 8 ) reverse( 12 1 10 3 0 4 14 16 17 11 6 15 2 8 7 5 13 9 ) Perm1362 = forward( 1 10 3 0 14 15 11 16 6 4 13 2 5 9 8 12 7 17 ) reverse( 3 0 11 2 9 12 8 16 14 13 1 6 15 10 4 5 7 17 ) Dumping permutations: Perm560 = forward( 15 5 13 0 14 2 4 10 9 6 16 8 3 7 1 17 11 12 ) reverse( 3 14 5 12 6 1 9 13 11 8 7 16 17 2 4 0 10 15 ) Perm1838 = forward( 8 11 0 9 7 15 2 16 17 13 10 3 12 14 6 1 5 4 ) reverse( 2 15 6 11 17 16 14 4 0 3 10 1 12 9 13 5 7 8 ) Perm1515 = forward( 13 4 11 14 0 17 3 16 8 10 1 12 9 5 6 2 7 15 ) reverse( 4 10 15 6 1 13 14 16 8 12 9 2 11 0 3 17 7 5 ) Dumping permutations: Perm569 = forward( 6 14 4 9 5 11 13 1 0 15 7 17 12 16 10 8 2 3 ) reverse( 8 7 16 17 2 4 0 10 15 3 14 5 12 6 1 9 13 11 ) Perm1676 = forward( 13 10 3 12 14 6 1 5 4 8 11 0 9 7 15 2 16 17 ) reverse( 11 6 15 2 8 7 5 13 9 12 1 10 3 0 4 14 16 17 ) Perm1524 = forward( 4 13 2 5 9 8 12 7 17 1 10 3 0 14 15 11 16 6 ) reverse( 12 9 2 11 0 3 17 7 5 4 10 15 6 1 13 14 16 8 )
By altering the Galois sequences (some permutations here and there), more results are obtained. So far, I haven't found better scores. I'll continue a bit, then try another approach.
.
Note : all "hits" go in quartets, I don't know yet why, but we find the same deltas : 9 between a pair of results and 171 between extremes... at least for the permutation number of the 1st level.
.
Source code is there : PermParam_20251226.tgz
.
.
.
Quadrupling the number of sequences, using xors (that do some swap actually), I get this one:
14 169 188 14 6 14 8 - 840 812 5745 Perm840 = forward( 2 7 0 6 9 1 15 13 12 3 16 5 17 14 4 8 10 11 ) reverse( 2 5 0 9 14 11 3 1 15 4 16 17 8 7 13 6 10 12 ) Perm812 = forward( 1 10 15 8 14 17 9 5 3 2 11 6 13 7 4 12 16 0 ) reverse( 17 0 9 8 14 7 11 13 3 6 1 10 15 12 4 2 16 5 ) Perm5745 = forward( 14 1 8 10 0 5 15 16 12 13 6 11 17 9 2 4 3 7 ) reverse( 4 1 14 16 15 5 10 17 2 13 3 11 8 9 0 6 7 12 )
It's imbalanced but still looks nice.
- Encoder avalanche: between 6 and 14
- Decoder avalanche : between 8 and 14
- 188/18 > 10 (> 9)
This is achieved by expanding the Galois sequences with XOR by a number (between 1 and 3) to create alternate versions. I get 7776 sequences, more opportunities for cross-checking and finding happy numerical accidents.
There is also the balanced ones:
14 188 168 14 7 14 7 - 1965 7515 4021 14 188 168 14 7 14 7 - 1974 7677 4030 14 188 168 14 7 14 7 - 2127 7506 4183 14 188 168 14 7 14 7 - 2136 7668 4192 Perm1965 = forward( 3 5 9 17 16 10 15 12 1 2 0 14 6 7 13 8 11 4 ) reverse( 10 8 9 0 17 1 12 13 15 2 5 16 7 14 11 6 4 3 ) Perm7515 = forward( 17 2 11 0 6 16 8 9 10 14 1 7 13 15 5 12 4 3 ) reverse( 3 10 1 17 16 14 4 11 6 7 8 2 15 12 9 13 5 0 ) Perm4021 = forward( 4 17 6 5 1 15 7 14 16 13 0 9 10 8 12 2 3 11 ) reverse( 10 4 15 16 0 3 2 6 13 11 12 17 14 9 7 5 8 1 ) Perm1974 = forward( 12 14 0 8 7 1 6 3 10 11 9 5 15 16 4 17 2 13 ) reverse( 2 5 16 7 14 11 6 4 3 10 8 9 0 17 1 12 13 15 ) Perm7677 = forward( 14 1 7 13 15 5 12 4 3 17 2 11 0 6 16 8 9 10 ) reverse( 12 1 10 8 7 5 13 2 15 16 17 11 6 3 0 4 14 9 ) Perm4030 = forward( 13 8 15 14 10 6 16 5 7 4 9 0 1 17 3 11 12 2 ) reverse( 11 12 17 14 9 7 5 8 1 10 4 15 16 0 3 2 6 13 ) Perm2127 = forward( 2 0 14 6 7 13 8 11 4 3 5 9 17 16 10 15 12 1 ) reverse( 1 17 0 9 8 10 3 4 6 11 14 7 16 5 2 15 13 12 ) Perm7506 = forward( 8 11 2 9 15 7 17 0 1 5 10 16 4 6 14 3 13 12 ) reverse( 7 8 2 15 12 9 13 5 0 3 10 1 17 16 14 4 11 6 ) Perm4183 = forward( 13 0 9 10 8 12 2 3 11 4 17 6 5 1 15 7 14 16 ) reverse( 1 13 6 7 9 12 11 15 4 2 3 8 5 0 16 14 17 10 )
And now I understand why I get these deltas of 9 : the permutations are identical, rotated/offset by 9 because the tiles are symmetrical too, so the whole permutations are +9 everywhere... It's obvious from Perm1965 vs Perm1974.
-
Brute-forcing the permutations
12/25/2025 at 08:33 • 0 commentsThe manual design is getting tedious, I have to automate it.
The final form (VHDL source code) will be something like, for the encoder :
Avalanche_D Permutation_P1 Avalanche_E Permutation_P2 Avalanche_D Permutation_P3 Avalanche_E
For now, P1=P3 for the ease of design but it doesn't have to be so.
The permutation can be a cyclical interleaving but the parameters must be determined and it might be too "regular".
Then a Galois sequence is a natural choice because it is not too regular and can be reversed.
By chance, we have 18 bits and 18+1=19 is a prime number ! so the generators are 2;3;10;13;14;15
So for each of the 3 layers, we have 6 sequences to test, but each sequence must also be "rotated" for the 18 bits, 6*18=108 combinations. This makes 108×108×108=1,259,712 combinations to test!It is possible but not practical with GHDL. I must code it in C, along with the figures of merit. I can then use __builtin_popcount(x) and other things directly and scan the whole range in a few minutes.
....
OK there is one more parameter to add to the generators : offset and index are different so each layer has 6×18×18=1944 combinations (should be all different). The 3 layers amount to 7,346,640,384 tests... so yeah I'll run that on 6 cores or something, and I'll strip all the computations down to the absolute minimum.
...
But Galois sequences have some lousy patterns:
Generator[0] = 2 : 1, 2, 4, 8, 16, 13, 7, 14, 9, 18, 17, 15, 11, 3, 6, 12, 5, 10 Generator[1] = 3 : 1, 3, 9, 8, 5, 15, 7, 2, 6, 18, 16, 10, 11, 14, 4, 12, 17, 13 Generator[2] = 10 : 1, 10, 5, 12, 6, 3, 11, 15, 17, 18, 9, 14, 7, 13, 16, 8, 4, 2 Generator[3] = 13 : 1, 13, 17, 12, 4, 14, 11, 10, 16, 18, 6, 2, 7, 15, 5, 8, 9, 3 Generator[4] = 14 : 1, 14, 6, 8, 17, 10, 7, 3, 4, 18, 5, 13, 11, 2, 9, 12, 16, 15 Generator[5] = 15 : 1, 15, 16, 12, 9, 2, 11, 13, 5, 18, 4, 3, 7, 10, 17, 8, 6, 14The 18s are aligned, right in the middle, reminding me that the sequence is symmetrical :-/
OTOH we have to start somewhere since 18! = 6.4E15
My Galois generator can already generate 1944 sequences but that's less than 1 billionth of the sequence space, and I can't scan it exhaustively. It's possible to do 1944^2=3779136 by permuting two of these sequences. Then, it's possible to compute the pipeline up to some point, for the 18 interesting values, and be more thorough at the last stage.
Some permutation table would help too, though I'm not sure if it would slow things down instead, because the LUT would occupy about 1MiB. Making the array would be worth it only if it is used more than a million times but it's unlikely. However, the 9-bit tiles fits in 2K bytes and it's perfect.
....
C-ing...
...
And I can generate 3.7 million permutations in about 0.24 second, using 3 stages of increasing buffers.
#include <stdlib.h> #include <stdio.h> #define GENCOUNT (6) #define BITS (18) #define MODULUS (19) #define PERMS (GENCOUNT*BITS*BITS) // 1944 unsigned char generators[GENCOUNT]={ 2, 3, 10, 13, 14, 15 }; unsigned char sequences[GENCOUNT][BITS]; unsigned char perms[PERMS][BITS]; unsigned char T[BITS]; static inline void combine_perm( unsigned char* perm_val, unsigned char* perm_index, unsigned char* perm_dst ) { for (unsigned int i=0; i<BITS; i++) perm_dst[i] = perm_val[perm_index[i] & 31]; } int main(int argc, char **argv) { for (unsigned int gen = 0; gen < GENCOUNT; gen++) { unsigned int generator=generators[gen]; unsigned int num=1; for (unsigned int index=0; index<BITS; index++) { sequences[gen][index] = num; num = (num * generator) % MODULUS; } } unsigned int perm=0; // Scan 18*18*6=1944 sequences for ( unsigned int gen = 0; gen < GENCOUNT; gen++) { for ( unsigned int index = 0; index < BITS; index++) { for (unsigned int offset = 0; offset < BITS; offset++) { unsigned int i=index; unsigned int k=0; do { // convert Galois domain (which excludes 0) to bit index domain unsigned int j=sequences[gen][i]-1; j += offset; if (j >= BITS) j -= BITS; // wrap around / modulo perms[perm][k++]=j; i++; if (i>=BITS) i=0; // circular addressing } while (i!=index); perm++; } } } for (unsigned int i=0; i < PERMS; i++) { for (unsigned int j=0; j < PERMS; j++) { combine_perm(perms[i], perms[j], T); for (unsigned int k=0; k < BITS; k++) putchar(T[k]+'a'); putchar('\n'); } } return EXIT_SUCCESS; }... of which only 1/36th are unique (104976) :-/
So i'll stay with 1944*1944*1944 = 7,346,640,384 as exhaustive scan, then I'll switch to pure random-driven permutations with reductions...
-
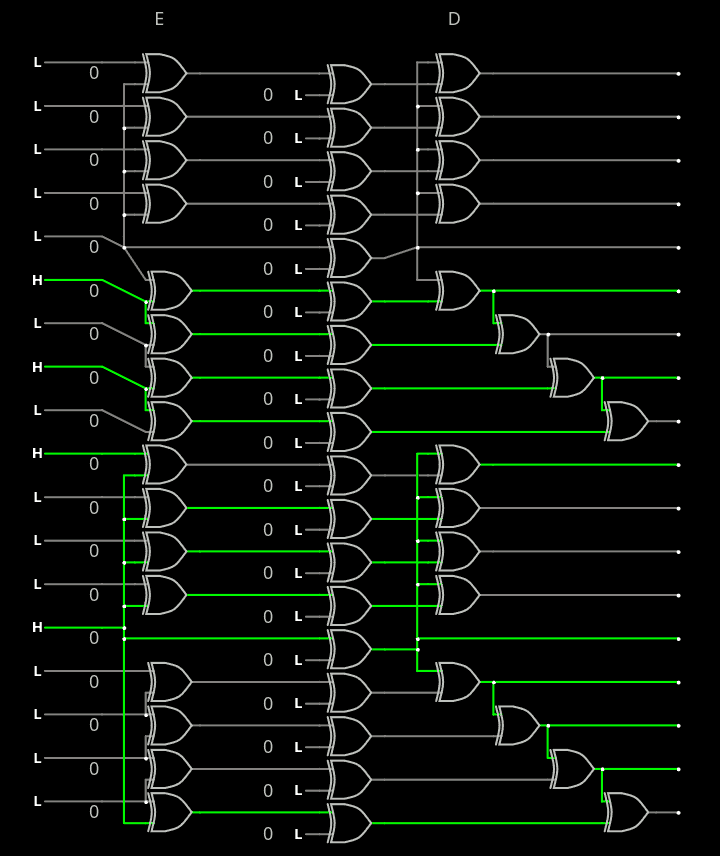
MaxHam gen2
12/25/2025 at 03:28 • 0 commentsThe previous attempt was very nice and taught me things, which I'll try to distill again, as I start coding it. Several insights affect this reboot:
- I wanted to avalanche way too much early on
- I should mix more at the first/outer layer
- avoid "cancellation" by detecting "loops" of XOR that break the avalanches
- alternate layer types so mixing is spreadier on the emitter.
- 4 or 5 layers should be OK to reach H9 on both sides
So we'll start with the "outer" layer:
![]()
(please excuse the flaw at the lower-left quadrant)
The Encoder layers stack becomes EDEDE, and decoder DEDED.
For DE:DE, we have this sandwich:
![]()
Avalanche for D-E: 1, 1, 1, 1, 2, 2, 2, 2, 6, 6, 6, 7, 8, 8, 9, 10, 13, 13
Avalanche E-D : 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 4, 4, 5, 5, 6, 6, 12, 12
Now what can we do ? Copy-paste of course ! With a little permutation that will associate the low avalanches with the high ones, and vice versa.
![]()
The Permutation P is reversed by S, which are both used 2×, and the intermediary Q is reversed by T. So overall the complexity is kept low through the duplications.
Encoder: DPE-Q-DPE
Decoder: DSE-T-DSEOnce you have the 9-bit tiles, they are duplicated and linked by permutations...
The result is still 64 XOR gates and a quite powerful avalanche, both forward and backward. However one of the input avalanches only to 2 bits on the transmission side...
Sender: 2, 5, 7, 7, 8, 8, 9, 9, 9, 10, 10, 11, 11, 12, 13, 13, 13, 13
Receiver: 6, 6, 6, 6, 6, 7, 7, 9, 10, 10, 10, 10, 11, 11, 11, 11, 12, 12
The sender has a bad bit with only 2 avalanches, which could be tied to the C/D bit. But that's a sub-optimal approach...
There are two ways to go forward:
- add another layer. This increases latency, cost, complexity...
- explore the design space with an exhaustive method: let a computer generate many permutations and find the best parameters. This looks like the way to go...
-
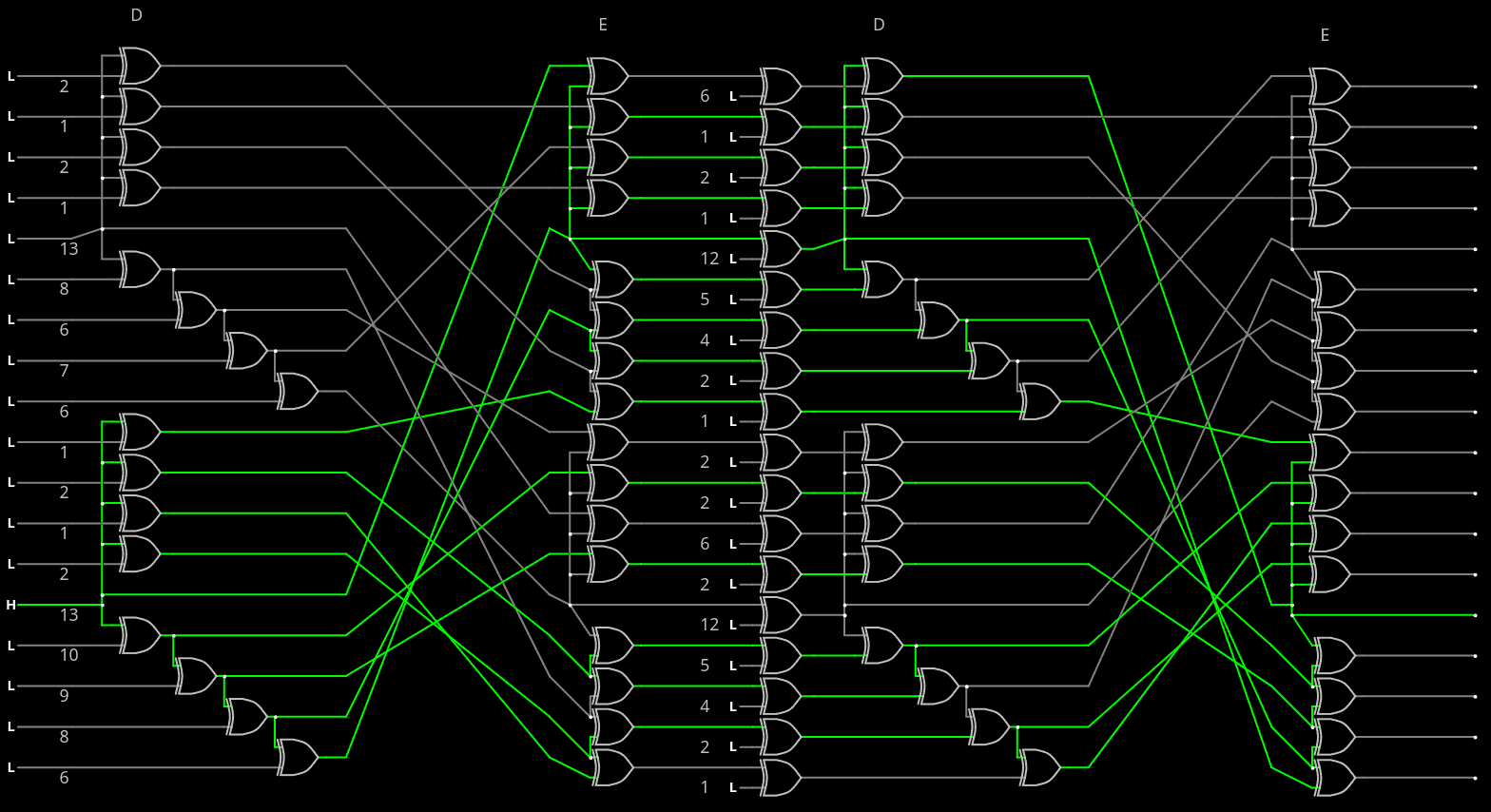
Hamming distance maximiser
12/23/2025 at 00:11 • 0 commentsA better 3-layers error propagator :
![]()
Avalanche from a single-bit error can reach 14, and only one affects only 8. That's a success.
However a whole bunch of inputs (7) still flip only 2 transmitted bits. In order to boost the avalanches there, the encoder should have a cascade too...
So here is the new encoder, with its two cascades to mitigate the poor effect on the line.
![]()
Two inputs only affect 4 bits. These can be allocated to the CD and MSB bits.
Notice that from the data available, ALL errors with 1, 2, 3, 5, 12, 13, 14, 15, 16, 17 and 18 bits will flip at least 2 decoded bits.
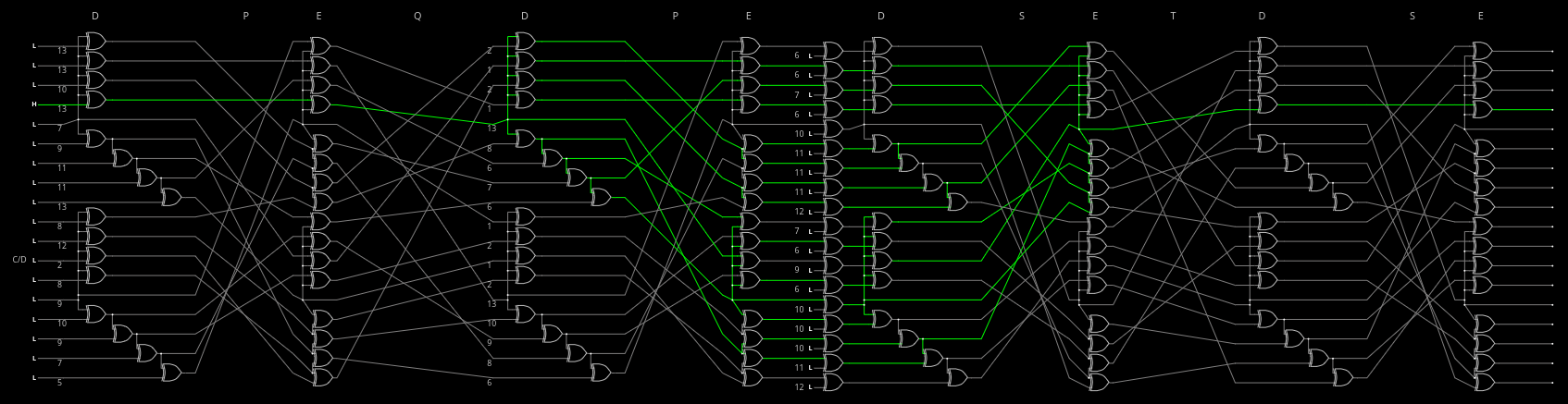
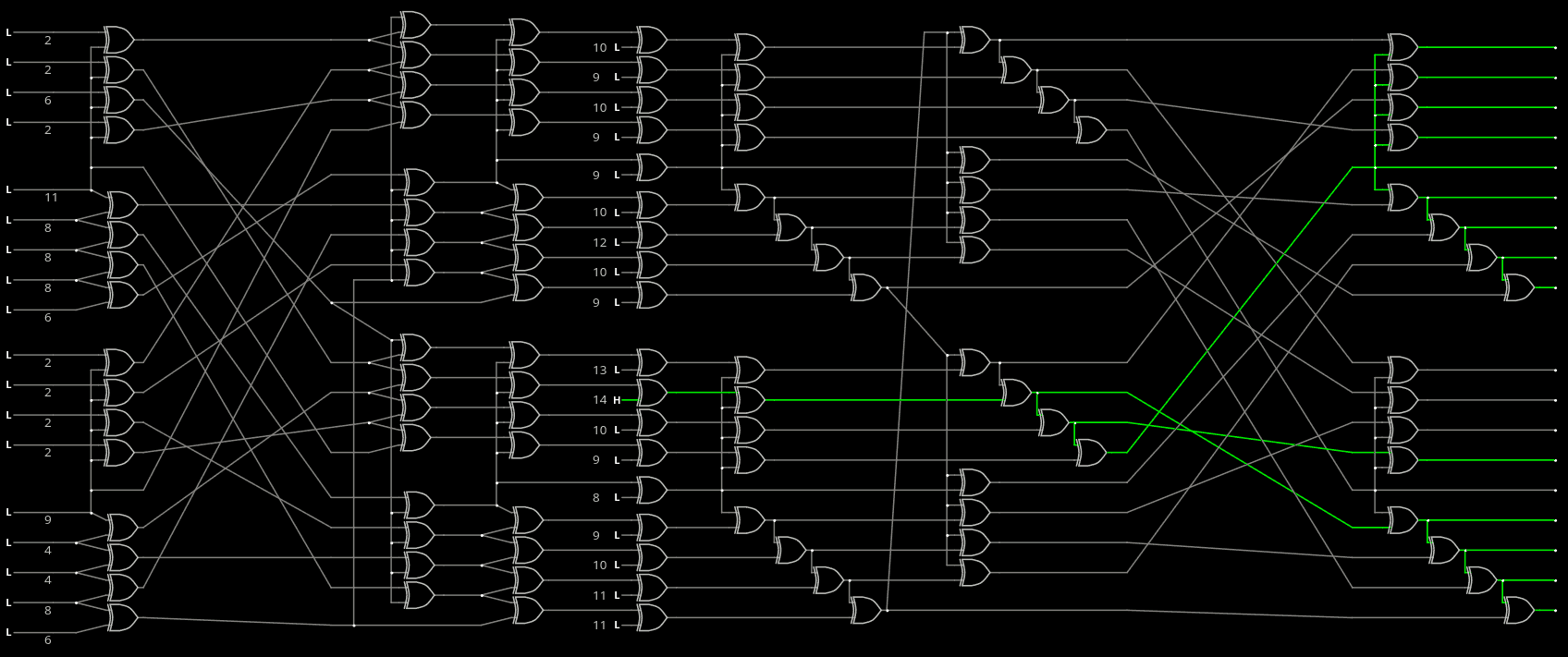
The whole pipeline is getting insane:
![]()
Here is the link, I removed segments to keep the URL working.
Total gates count for the encoder and the decoder : 64 XOR each. That's not insignificant but it's still way "cheaper" than the tens of words of FIFO that it saves, and even though the immediate error latency increases by one or two cycles, the worst cases are considerably reduced, without having to increase the avalanche in the PEAC scrambler.
- Avalanche input-to-output: 4,4,6,6,6,6,6,6,7,8,8,8,8,8,9,9,10,11
- Avalanche input-to-output: 5,5,6,7,7,8,9,9,9,9,9,9,9,9,9,10,11,11
The worst-case error avalanche has decreased... but it's still manageable and it's a compromise for the size and the input avalanche. I'm sure there are better circuits but it's the best I can do in a day, it's a considerable improvement over the existing system.
And now, VHDL is calling.
miniMAC - Not an Ethernet Transceiver
custom(izable) circuit for sending some megabytes over differential pairs.
 Yann Guidon / YGDES
Yann Guidon / YGDES